苏科版七年级下册7.2 探索平行线的性质图文ppt课件

这是一份苏科版七年级下册7.2 探索平行线的性质图文ppt课件，共27页。PPT课件主要包含了复习回顾，交流合作探索发现，∵a∥b，a∥b，平行线性质1，平行线的性质等内容，欢迎下载使用。

平行线的判定方法是什么？
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
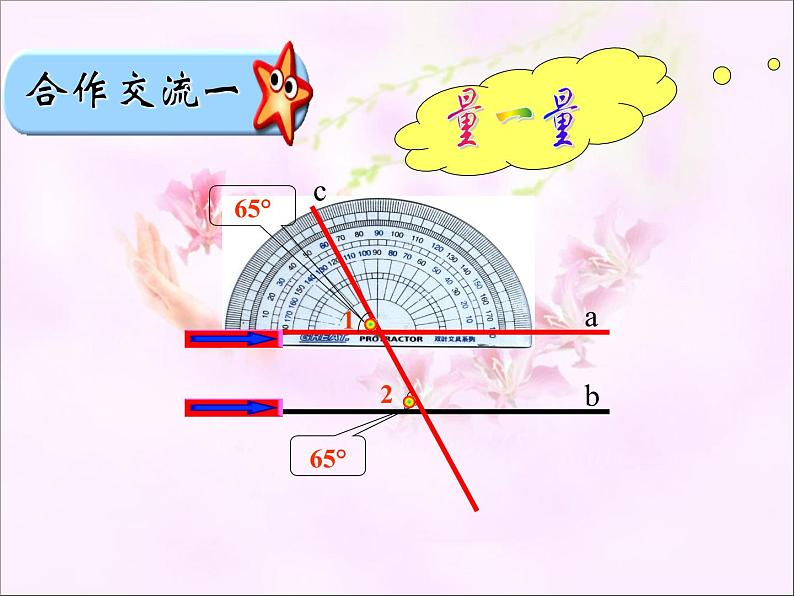
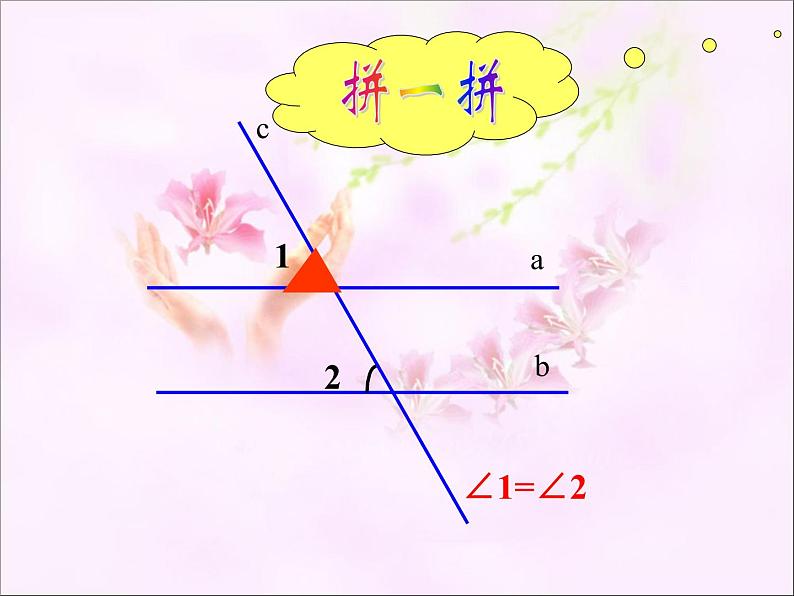
猜一猜∠1和∠2相等吗？
是不是任意一条直线去截平行线a、b 所得的同位角都相等呢？
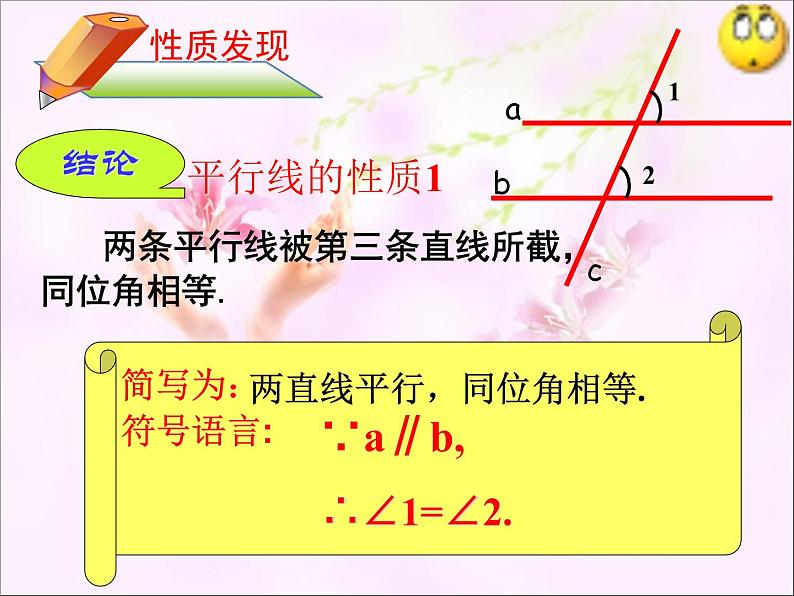
两直线平行，同位角相等.
两条平行线被第三条直线所截， 同位角相等.
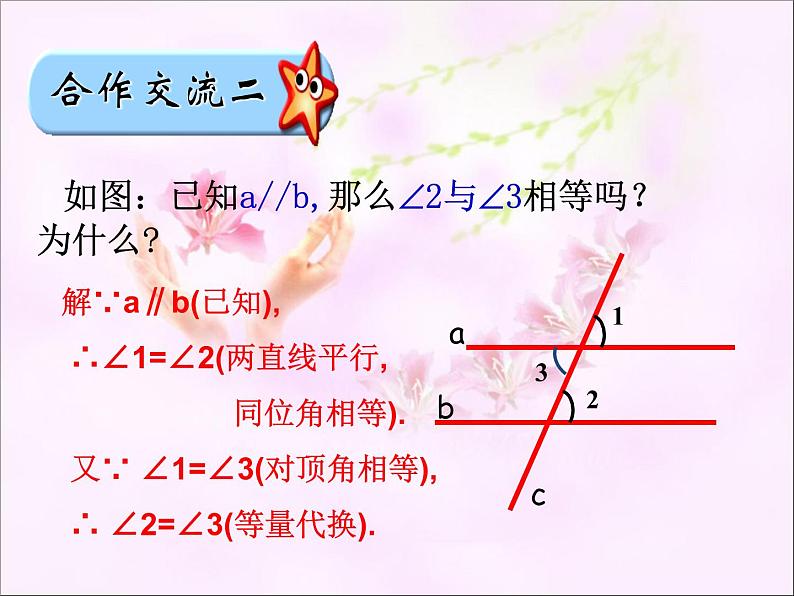
如图：已知a//b,那么2与3相等吗？为什么?
解∵a∥b(已知), ∴∠1=∠2(两直线平行, 同位角相等). 又∵ ∠1=∠3(对顶角相等), ∴ ∠2=∠3(等量代换).
两直线平行，内错角相等.
两条平行线被第三条直线所截， 内错角相等.
解： ∵a//b （已知）,
如图,已知a//b,那么2与4有什么关系呢？为什么?
∴ 1=  2（两直线平行， 同位角相等）.
∵  1+  4=180° （邻补角定义）,
∴ 2+  4=180° （等量代换）.
两直线平行，同旁内角互补.
两条平行线被第三条直线所截， 同旁内角互补.
∴ 2+  4=180°.
变式2:已知∠3 =∠4，∠1=47°,求∠2的度数？
∴∠ 2= 470（ ）
解：∵ ∠3 =∠4( )
∴a∥b( )
又∵∠ 1 = 470 ( )
两直线平行，同位角相等
同位角相等,两直线平行
如图在四边形ABCD中,已知AB∥CD,∠B = 600.①求∠C的度数;②由已知条件能否求得∠A的度数?
解: ① ∵ AB∥CD(已知),∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).又∵ ∠B = 600 (已知),∴∠C = 1200 (等式的性质).
②根据题目的已知条件,无法求出∠A的度数.
探究:两直线平行,同位角有什么关系? 相等
如图，直线a∥b，（1）测量同位角∠1和∠5的大小，它们有什么关系？
　简单地说：两直线平行，同位角相等．
几何语言表述: ∵a∥b(已知)∴∠１＝∠2（两直线平行，同位角相等）
两条平行线被第三条直线所截，同位角相等．
　两直线平行，同位角相等． 几何语言表述: ∵a∥b(已知) ∴∠1=∠2(两直线平行,同位角相等)
猜想:两直线平行，内错角、同旁内角有怎么关系呢？相互讨论一下.
性质１：两直线平行，同位角相等．性质２：两直线平行，内错角相等．性质３：两直线平行，同旁内角互补．
利用性质1来说明性质2和性质3
已知: a ∥ b , 请说明∠2=∠3.
∵ a ∥ b (已知)∴∠1=∠2( )
∵ ∠1=∠3( )
如图，(1)∵ a ∥ b (已知) ∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知) ∴ ∠2____∠3 (  )
(3)∵ a ∥ b (已知) ∴ ∠2＋∠4=____ (     )
两直线平行，内错角相等
两直线平行，同旁内角互补
已知角之间的关系(相等或互补)，得到两直线平行的结论是平行线的判定。 已知两直线平行，得到角之间的关系(相等或互补)的结论是平行线的性质。
1、如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度?
∵ ∠2=∠1 (对顶角相等)∴ ∠2=∠1 =54°∵ a∥b(已知)∴ ∠4=∠1=54°(两直线平行,同位角相等) ∠2+∠3=180°(两直线平行,同旁内角互补)∴ ∠3= 180°－ ∠2= 180° － 54°=126°即 ∠2=54° ，∠3=126°， ∠4=54°。
（1）∵∠ADE=60 ° ∠B=60 °
(同位角相等，两直线平行)
(两直线平行，同位角相等)
2、已知　∠ADE=60 ° ∠B=60 °∠AED=40°证：（１）DE∥BC　　（２） ∠C的度数
同位角相等内错角相等同旁内角互补
两直线平行同旁内角互补