初中数学苏科版七年级下册8.1 同底数幂的乘法课堂教学课件ppt

这是一份初中数学苏科版七年级下册8.1 同底数幂的乘法课堂教学课件ppt，共20页。PPT课件主要包含了回顾思考，乘方的意义，探究新知，自主探究，底数相同，10m+n，m×10n，2m+n，8m+n，试一试等内容，欢迎下载使用。

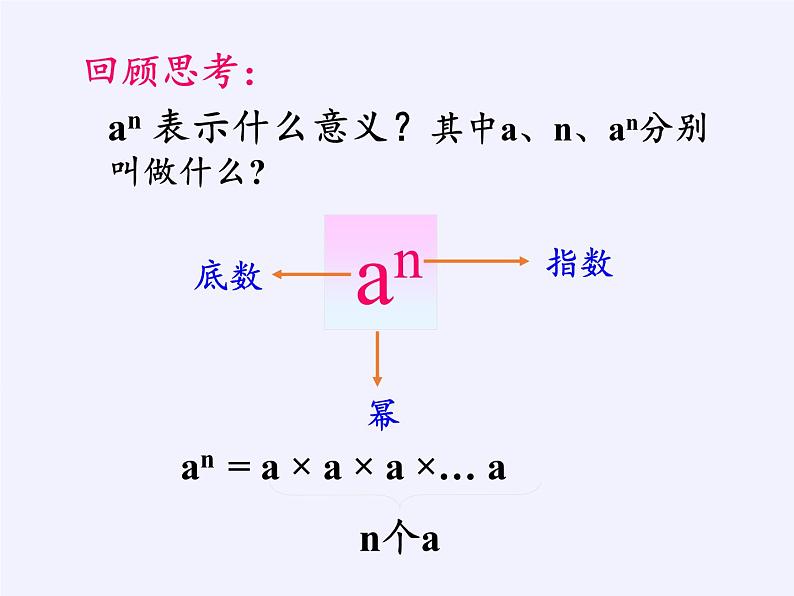
an 表示什么意义？其中a、n、an分别叫做什么?
an = a × a × a ×… a n个a
(1)105表示什么？
(1)105 = . 
10×10×10×10×10
(2) 10×10×10×10= .
(2)10×10×10×10可以写成什么形式?
观察：104与105 、a4与a5、10m与10n、am与an,每组幂之间有什么相同点？
我们把底数相同的幂叫做同底数幂。
找一找：同底数幂的一组是（ ）A 24与34 B a4与b5 C （a+b）m与(b+a)n D 53与35
根据乘方的意义，解答下列各题. 102 ×104 = （ 10 × 10 ） × （10× 10 × 10 × 10 ） = 10 （ ） ； 104 × 105 = . = 10（ ） ； 103× 105 = . = 10（ ）
（10×10 ×10 ×10 )×( 10× 10 × 10 ×10× 10 )
（10×10 ×10 )×( 10× 10 × 10 ×10× 10 )
如何计算10m× 10n(m,n为正整数）？
= 10× 10×… ×10
（10× 10× … × 10）
（ 10× 10×… ×10）
2m× 2n （ m,n为正整数） 等于什么？
8m× 8n呢（ m,n为正整数） ？
猜想: am · an= (m、n为正整数)
am · an =
am · an = am+n (m、n为正整数)
想一想： 当三个或三个以上同底数幂相乘时，是否也 　 具有这一性质呢？
如 am·an·ak =
（m、n、k都是正整数）
观察am · an = am+n (m、n为正整数)，此式子的左边与右边的底数和指数，各有什么特点？
注:公式中的a可代表一个数、字母、式子.
下面的计算是否正确？若有错误，应该怎样改正？
例1.计算,结果用幂的形式表示：
（1） a · a6 （2）xm · x2n+1 （3）(-2)6 ·(-2)8 （4）- 35· (-3)5 · (-3)
解：（ 1 ） a · a6 =a1+6=a7
（2） xm · x2n+1 =xm+2n+1
（3） (-2)6 ·(-2)8=(-2)6+8=(-2)14=214
（4 ) -35 ·(-3) 5 · (-3) =（-3）5 · （-3)5 · (-3) =（-3）5+5+1 =（-3）11 = -3 11
(－3)5和－35有什么不同？
（1）(－3)12 × (－3)3 ； （2）x · x7 .
(3)( — )5·(— )6·( — )
(m-n)3· (m-n)2
变式： (m-n)3· (n-m)2
解：原式 = (m-n)2+3
解：原式 = (m-n)3· (n-m)2 =(m-n)2+3 =(m-n)5
例3：计算 (1) x3·x4 + x3·x3·x  
（1）原式=x7+x7
(2) 23×4×8 ×16（结果用幂的形式表示.）
(2) 原式=23×22 × 23 × 24
（结果用科学计数法的形式表示.）
知识　
“特殊→一般→特殊” 认知规律
同底数幂相乘，　底数　　 指数　 am · an = am+n (m、n正整数)am·an·ak = am+n+k （m、n、k都是正整数）
注意：1.a=a1 2.公式中的a可代表一个数、字母、式子等. 3.公式可以逆用，即am+n= am · an （m、n都是正整数）
课堂检测1.   计算：
（1） a8 ·a3
（2） —x5 ·x · x2
（3） a·a7—a4·a4
2. 已知2m· 2m·4=28,则m的值是 .
（5）(a－b)3 · (b－a)2
3. 已知2m=3， 2n=4,则2m+n+1的值是 .
课本P48习题8.1第3、4、5题．