初中数学人教版八年级下册19.2.2 一次函数精品课件ppt

这是一份初中数学人教版八年级下册19.2.2 一次函数精品课件ppt，文件包含《1922一次函数第2课时》同步精品课件pptx、《1922一次函数第2课时》同步精品教案doc等2份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
1.会画一次函数的图象，能根据一次函数的图象理解一次函数的增减性。(重点）2.能从图象角度理解正比例函数与一次函数的关系。（难点）3.能灵活运用一次函数的图象与性质解答有关问题。
同学们，什么是正比例函数，什么是一次函数？
形如___ 的函数，叫做正比例函数；
形如__ 的函数，叫做一次函数；
当b=0时，y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数.
y=kx（k是常数，k≠0）
y=kx+b(k,b是常数，k≠0)
还记得正比例函数的图象和性质吗？
正比例函数的图象：一条经过 点的 ；正比例函数的性质： k＞0，y 随x 的增大而增大； k＜0，y 随 x 的增大而减小．
【思考】一次函数的图象和性质又是怎样的呢？
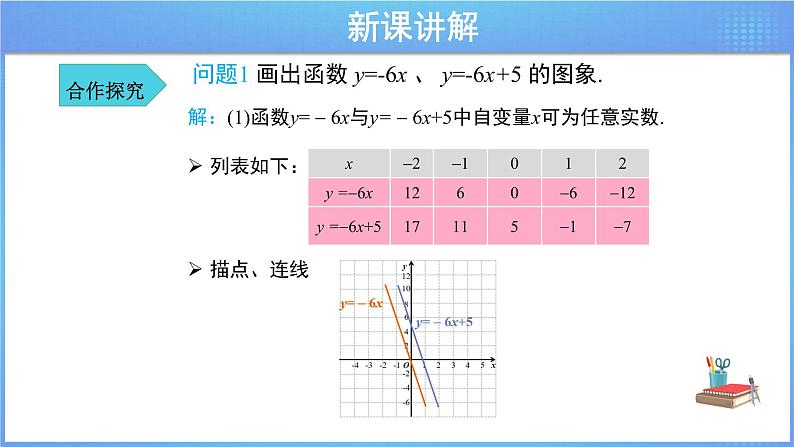
问题1 画出函数 y=-6x 、 y=-6x+5 的图象.
解：(1)函数y=  6x与y=  6x+5中自变量x可为任意实数.
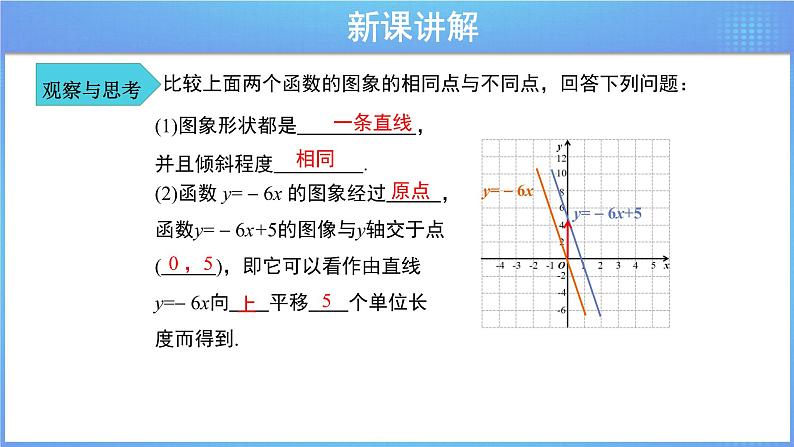
比较上面两个函数的图象的相同点与不同点，回答下列问题：
①一次函数 y＝kx+b(k≠0)的图象是一条直线， 我们称它为直线 y＝kx+b(k≠0)．
(注：b＞0时，向上平移；b＜0时，向下平移.)
结合上述结果，说一说一次函数y=kx+b(k≠0)的图像是什么形状，它与直线y=kx(k≠0)有什么关系？
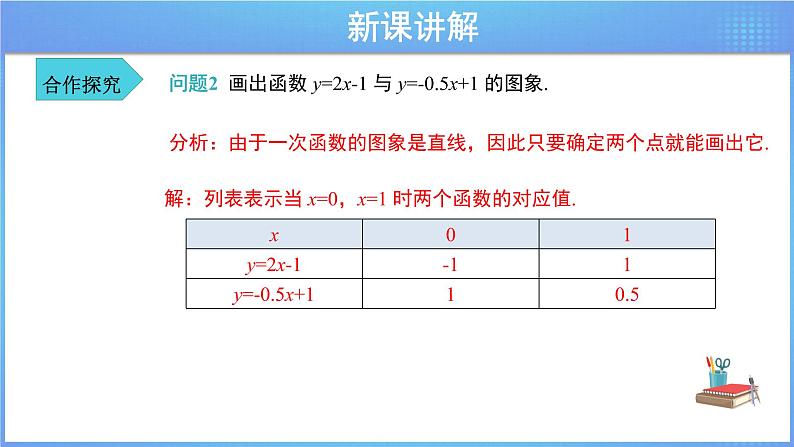
问题2 画出函数 y=2x-1 与 y=-0.5x+1 的图象.
分析：由于一次函数的图象是直线，因此只要确定两个点就能画出它.
解：列表表示当 x=0，x=1 时两个函数的对应值.
过点（0，-1）与点（1，1）画出直线y＝2x－1；过点（0，1）与点（1 ，0.5）画出直线y＝-0.5x+1.
　一般用(0,0),(1，k)来画正比例函数y=kx(k≠0）图象，那么一次函数呢？
令x=0，则得y=b，图象与y轴交于(0，b)；
画出函数y=x+1， y=  x+1， y=2x+1，y=  2x+1的图象．
列表表示当x=0，x=1时两个函数的对应值.
一次函数解析式y=kx+b(k，b是常数，k≠0)中，k的正负性对函数图象有什么影响？
当k＞0时，直线y=kx+b从左至右上升，即y随x的增大而增大；
当k＜0时，直线y=kx+b从左至右下降，即y随x的增大而减小.
一次函数解析式y=kx+b(k，b是常数，k≠0)中，b的正负性对函数图象有什么影响？
从左至右上升，交点在y轴正半轴.
从左至右上升，交点在原点.
从左至右上升，交点在y轴负半轴.
一次函数y=kx＋b中，k，b的正负对函数图象性质有什么影响？
从左至右下降，交点在y轴正半轴.
从左至右下降，交点在原点.
从左至右下降，交点在y轴负半轴.
例1 已知点P1(x1，y1)，P2(x2，y2)是一次函数y=-0.5x+3图象上的两点，下列判断中，正确的是( )
A.y1＞y2 C.当x1＜x2时，y1＜y2
B. y1＜y2 D.当x1＜x2时，y1＞y2
解析:根据一次函数的性质: 当k＜0时，y随x的增大而减小，所以D为正确答案．
提示：反过来也成立：y越大，x就越小．
例2 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值：（1）函数值y 随x的增大而增大；（2）函数图象与y 轴的负半轴相交；（3）函数的图象过第二、三、四象限；
解：(1)由题意得1-2m>0，解得
(2)由题意得1-2m≠0且m-10，经过一、二、三象限，y随x的增大而增大；②b0，经过一、二、四象限，y随x的增大而减小；②b0，经过一、二、三象限，y随x的增大而增大；②b0，经过一、二、四象限，y随x的增大而减小；②b