初中数学苏科版九年级下册5.4 二次函数与一元二次方程说课ppt课件

这是一份初中数学苏科版九年级下册5.4 二次函数与一元二次方程说课ppt课件，共22页。PPT课件主要包含了知识回顾，yx2-4x+3，对称轴直线x2，当x＜1或x＞3时，y＞0，当1＜x＜3时，y＜0，x轴上方的图象，x轴下方的图象，数形结合思想等内容，欢迎下载使用。

抛物线y=ax2+bx+c与x轴有两个公共点
一、抛物线y=ax2+bx+c与x轴的交点个数 可由b2-4ac的符号决定。
二、抛物线y=ax2+bx+c与x轴的交点的横坐标 是一元二次方程ax2+bx+c=0的根。
抛物线y=ax2+bx+c与x轴有唯一公共点
抛物线y=ax2+bx+c与x轴没有公共点
(1)b2-4ac＞0
(2)b2-4ac =0
(3)b2-4ac ＜0
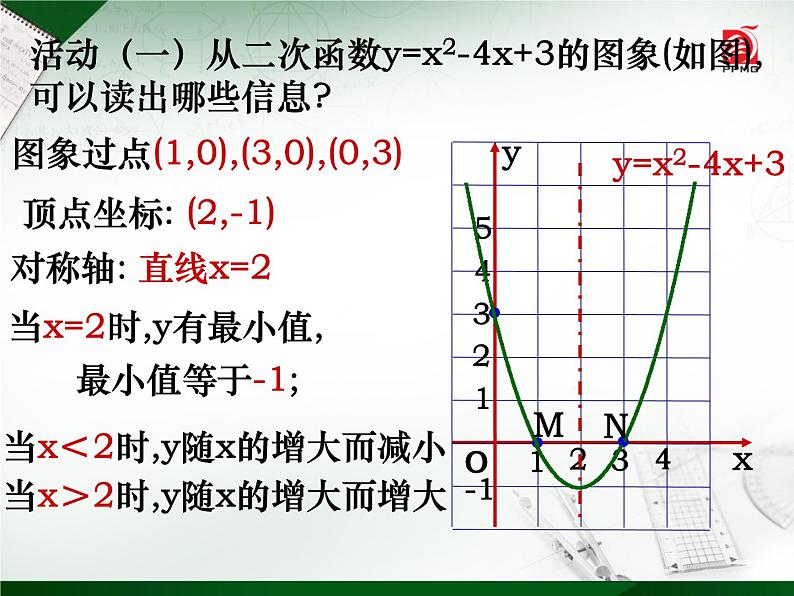
活动（一）从二次函数y=x2-4x+3的图象(如图),可以读出哪些信息?
图象过点(1,0),(3,0),(0,3)
当x=2时,y有最小值, 最小值等于-1;
当x＜2时,y随x的增大而减小
当x＞2时,y随x的增大而增大
顶点坐标: (2,-1)
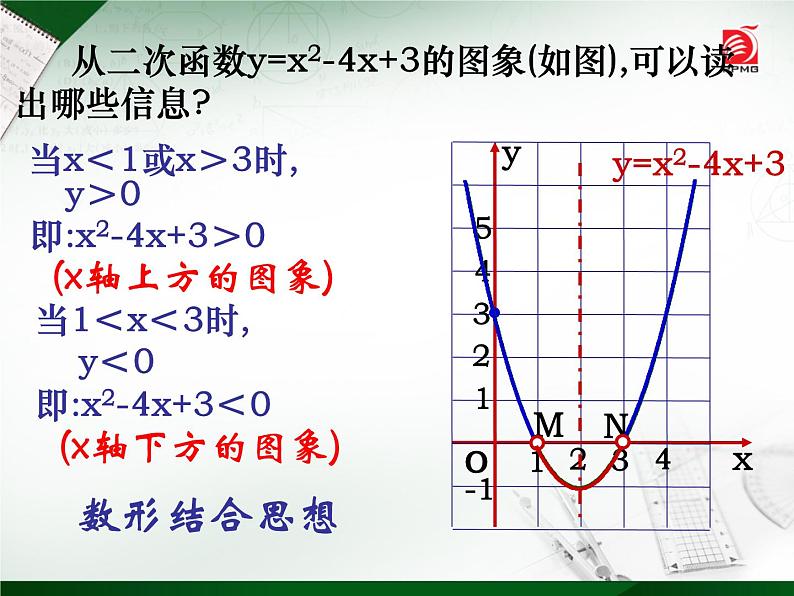
即:x2-4x+3＞0
即:x2-4x+3＜0
从二次函数y=x2-4x+3的图象(如图),可以读出哪些信息?
练习：1.二次函数 的图象如图所示，下列几个结论：①对称轴为x=2; ②当y≤0时,x＜0或x＞4；③函数解析式为 ；④当x≤0时，y随x的增大而增大. 其中正确的结论有 .(填上正确序号)
练习：2.如图所示的抛物线：当x=_________.时，y=0；当x<－2或x>0时， y_________0；当x在____________范围内时，y≥0；当x=________时，y有最大值_____.
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示， 根据图象解答下列问题.（1）写出方程ax2+bx+c=0的两个根； （2）写出不等式ax2+bx+c＞0的解集； （3）写出y随x的增大而减小的自变量x的取值范围； （4）若方程ax2+bx+c=k有两个不相等的实数根，求k的取值范围．
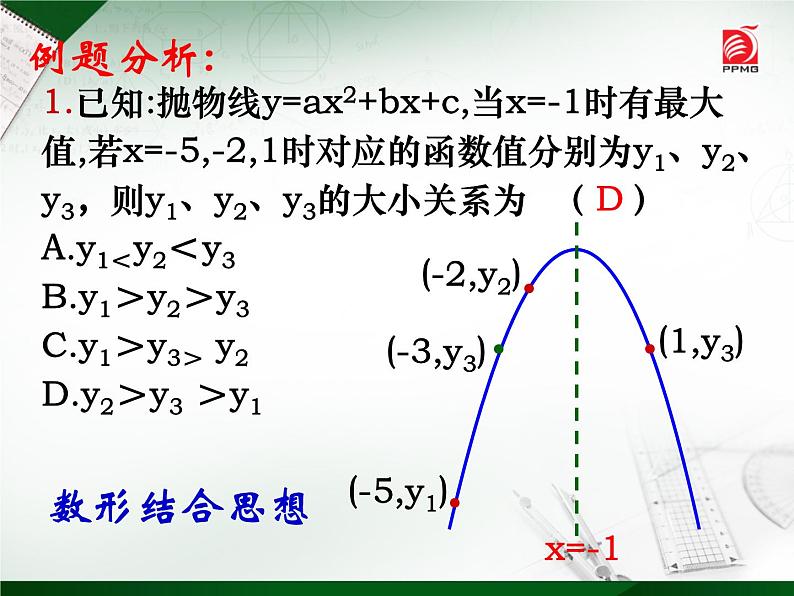
1.已知:抛物线y=ax2+bx+c,当x=-1时有最大值,若x=-5,-2,1时对应的函数值分别为y1、y2、y3，则y1、y2、y3的大小关系为 （ ）A.y1＜y2＜y3　　　　　　B.y1＞y2＞y3 　　　C.y1＞y3＞ y2 　　　　 D.y2＞y3 ＞y1
1.已知抛物线和直线在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点, P3(x3，y3)是直线上的点 ,且-1< x1 2.如图,已知:抛物线y1=ax2+bx+c与直线y2=kx+m相交于A(5,3)和B(2,-1).则当x满足条件 时,y1=y2;则当x满足条件 时,y1＞y2;
则当x满足条件 时,y1 ≤y2;
活动（二）已知二次函数y=x2+2x-5的图像你能探索方程x2+2x-5=0的根的取值范围吗？
问题1.观察图象,抛物线与x轴有两个公共点,说出他们横坐标分别在什么整数范围内?
-4＜x1＜-3, 1＜x2＜2
则一元二次方程的两个根就在-4与-3,1与2之间
这两个根分别是1.5和-3.5吗?
探索:利用二次函数y=x2+2x-5的图像,求方程x2+2x-5=0的近似根.
问题2.观察图象并借助于计算,你能探索x1与x2的 近似值?(精确到0.1)
探索:利用二次函数y=x2+2x-5的图象,求方程x2+2x-5=0的近似根.
当X=1.5时,y=0.25 ＞0.说明使y=0的x的值一定在1与1.5之间,即1 ＜x ＜1.5
当x=1.25时,y=-0.9375 ＜ 0.说明使y=0的x的值一定在1.25与1.5之间,即1.25 ＜x ＜1.5
当x=1.3时,y=-0. 71 ＜ 0.说明使y=0的x的值一定在1.3与1.5之间,即1.3 ＜x ＜1.5
当x=1.4时,y=-0. 24 ＜ 0.说明使y=0的x的值一定在1.4与1.5之间,即1.4 ＜x ＜1.5
5. 缩小范围到1.4 ＜x ＜1.5,由于要精确到 0.1,必须运算到0.01.
则1.40 ＜x ＜1.45∴使y=0的近似值为1.4
由上可得,方程x2+2x-5=0介于1与2之间的根x2的近似值为1.4(精确到0.1)
问题3.你能用同样的方法确定方程x2+2x-5=0的另一个根x1(精确到0.1)
根据上表中二次函数y=ax2+bx+c的自变量x 与函数值y的对应值,判断方程 ax2+bx+c=0(a≠0, a,b,c为常数)的一个解x的范围是 ( ) A.6＜x＜6.17 B. B. 6.17＜x＜6.18 C. 6.18＜x＜6.19 D. 6.19＜x＜6.20