数学九年级下册5.4 二次函数与一元二次方程多媒体教学课件ppt

这是一份数学九年级下册5.4 二次函数与一元二次方程多媒体教学课件ppt，共19页。PPT课件主要包含了y＝x2－2x－3，X10，X20，与x轴的公共点个数，一元二次方程根的个数，个不等根，b2-4ac＞0，个等根，b2-4ac＜0，b2-4ac0等内容，欢迎下载使用。

（1）解一元一次方程x＋1＝0；（2）画一次函数y ＝x ＋1的图像，并指出函数y ＝ x ＋1的图像与x轴有几个交点；（3）一元一次方程x ＋1＝ 0与一次函数y ＝x ＋1有什么联系？
5.4 二次函数与一元二次方程(1)
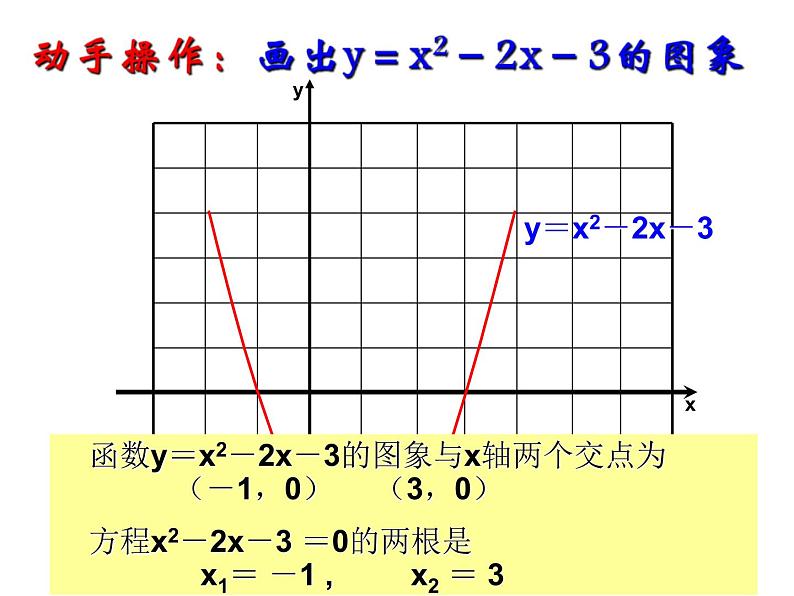
函数y＝x2－2x－3的图象与x轴两个交点为 （－1，0） （3，0）
方程x2－2x－3 ＝0的两根是 x1＝ －1 , x2 ＝ 3
你发现了什么？（1）二次函数y＝ax2＋bx＋c 与x轴的交点的横坐标就是当y＝0时 一元二次方程ax2＋bx＋c＝0的根;（2）二次函数与x轴的交点问题可以 转化为一元二次方程去解决.
探究一：图象与x轴的交点的坐标是什么？
例1. 求二次函数y＝x2＋4x－5的图象与x轴的交点坐标. 解：令y＝0 则x2＋4x－5 ＝0 解之得，x1＝ －5 ,x2 ＝ 1∴二次函数y＝x2＋4x－5的图象与x轴的 交点坐标为：（－5，0）（1，0）
结论一：若一元二次方程ax2+bx+c=0的两个根是x1、x2， 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A（ ）， B（ ）
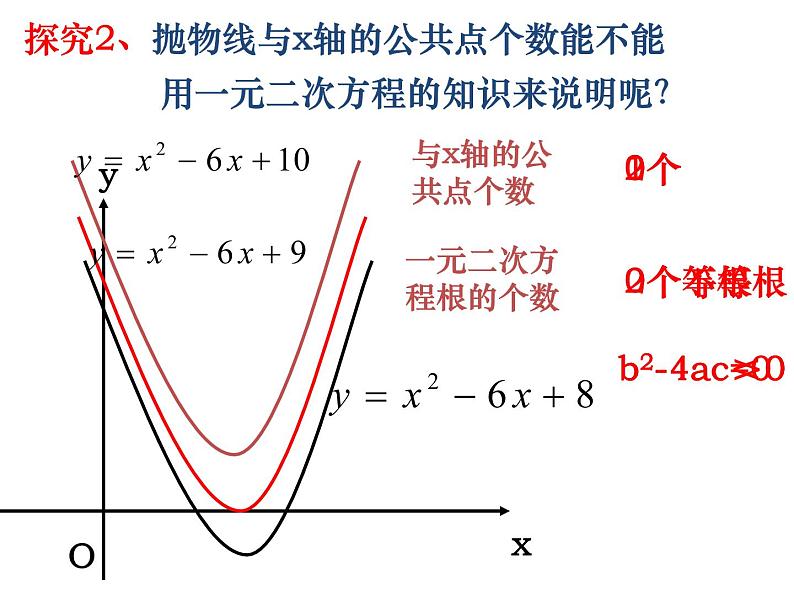
探究2、抛物线与x轴的公共点个数能不能 用一元二次方程的知识来说明呢？
一元二次方程ax2+bx+c=0有两个不等的实数根
抛物线y=ax2+bx+c与x轴有两个公共点
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明：
抛物线y=ax2+bx+c与x轴有唯一公共点
一元二次方程ax2+bx+c=0有两个相等的实数根
抛物线y=ax2+bx+c与x轴没有公共点
一元二次方程ax2+bx+c=0没有实数根
※b2-4ac＞0
※b2-4ac =0
※b2-4ac ＜0
例2.判断下列二次函数图象与x轴的交点情况 y＝x2－1；解：∵ b2－4ac＝02 －4×1×(－1) = 4 ＞0 ∴函数与x轴有两个交点 练习1不画图象判断下列函数的图象与x轴是否有公共点，并说明理由．(1)　y=x2-x (2)　y=-x2+6x-9(3) y=3x2+6x+11
例1．已知抛物线（1）当k取什么值时，抛物线与x轴有两个交点？（2）当k取什么值时，抛物线与x轴有一个公共点？并求出这个公共点的坐标．（3）当k取什么值时，抛物线与x轴没有公共点?
根据对应方程的根的情况，可以确定二次函数的图象与x轴的交点个数。
例2．已知：抛物线求证：此抛物线与x轴必有两个不同交点．
即证明对应方程中的b2-4ac＞0
例3.(1)已知二次函数y=x2-4x+k+2的图象 与x轴有公共点，求k的取值范围.
(2)已知二次函数y=kx2－7x－7的图象 与x轴有两个交点,则k的取值范围为 .
练习2、已知抛物线y=x2-6x+a, (1)顶点在x轴上，则a= ； (2)若抛物线与坐标轴有两个公共点则a= ；
1．已知抛物线 ．（1）求它与x轴交点A、B的坐标，与y轴交点C的坐标． （2）求△ABC的面积．
已知二次函数 （1）求证：对于任意实数m，该二次函数图象与x轴总有公共点． （2）若该二次函数图象与x轴有两个公共点A、B，且A点坐标为（1，0），求B 点的坐标．
已知抛物线 与坐标轴只有两个交点，求k的值．
联想：二次函数与x轴的交点个数可以借助 判别式解决，那么二次函数与一次 函数的交点个数又该怎么解决呢？ 例如: 二次函数y＝x2－2x－3和一次函数 y＝x＋2有交点吗？有几个？分析: 两个函数的交点是这两个函数的公共解， 先列出方程组，消去y后，再利用判别式 判断即可.
拓展： 二次函数y＝x2－x－3和一次函数 y＝x＋b有一个公共点（即相切）， 求b的值.解：由题意，得 消元，得 x2－x－3 ＝x＋b 整理，得x2－2x －（3 ＋ b） ＝0∵有唯一交点∴（－2）2 ＋4（ 3 ＋ b） ＝0解之得，b ＝－4
1. 若2，4是方程 的两个根， 则对应抛物线y＝ 的对称轴 是_________.