初中数学苏科版九年级下册5.1 二次函数教学演示ppt课件

这是一份初中数学苏科版九年级下册5.1 二次函数教学演示ppt课件，共21页。PPT课件主要包含了学习目标，合作探究，二次项系数是1，常数项是－4，一次项系数是－1，不是二次函数，二次函数，归纳新知等内容，欢迎下载使用。

1.二次函数的定义.2.根据实际问题列二次函数表达式.
新知一 二次函数的定义
定义：一般地，形如y=ax2+bx+c(a，b，c 是常数，且a ≠ 0)的函数叫做二次函数. 其中x 是自变量，y 是x 的函数，a，b，c 分别是函数表达式的二次项系数、一次项系数和常数项．
详解：二次函数的特殊形式：①只含二次项，即：y=ax2(b=0，c=0)；②不含一次项，即：y = ax2 + c (b=0，c≠ 0)；③不含常数项，即：y=ax2+bx(b≠0，c=0).
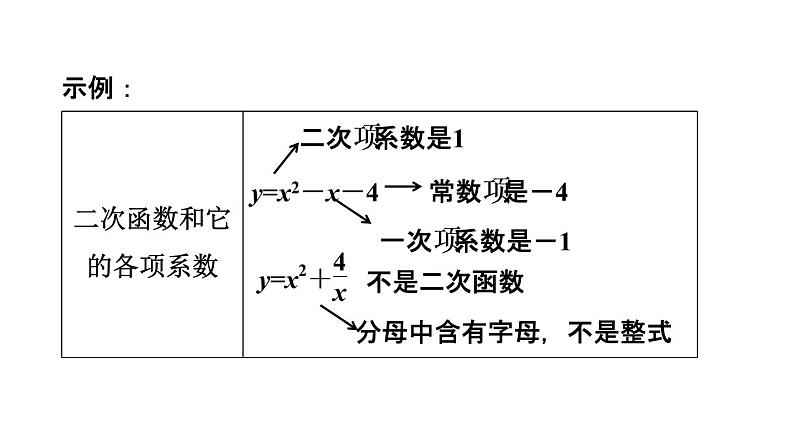
分母中含有字母，不是整式
2. 确定二次函数的“三要素”(1)含有自变量的代数式必须是整式；(2)化简后自变量的最高次数是2；(3)二次项系数不等于0.
[期末·淮安] 下列函数中属于二次函数的是( )
解题秘方：根据二次函数的定义，逐一分析四个选项，即可得出结论．
解：A. y ＝ x 是正比例函数；B. y＝ 2x2－1 是二次函数；C. y ＝ 根号内含有自变量，不是整式，故不是二次函数；D. y ＝ x2+ +1 分母中含有自变量，不是整式，故不是二次函数．故A、C、D 选项不符合题意，B 选项符合题意
将二次函数y=(x－2)(x－5) －3x 化为一般形式，并指出其二次项系数、一次项系数和常数项.
解题秘方：根据二次函数的一般形式y=ax2+bx+c(a，b，c 是常数，且a ≠ 0)，其中a，b，c 分别叫做二次项系数，一次项系数，常数项进行解答即可.
解：y=(x－2)(x+5)－3x=x2－10，二次项系数是1，一次项系数是0，常数项是－10.
特别提醒：二次函数表达式化为一般形式后才能确定各项系数，确定各项系数时不能遗漏这一项前面的符号.
[模拟·苏州] 若函数y ＝ 4x2+1 的函数值为5，则自变量x的值应为( )A. 1　　　 　B. － 1　　　C. ±1　 D.
解题秘方：把函数值y ＝ 5 代入函数表达式，然后解一元二次方程即可．
方法技巧：根据自变量值求函数值和根据函数值求自变量值，解题的关键是把给出的自变量值或函数值正确代入表达式，并准确计算．
解：根据题意，得4x2+1 ＝ 5，x2＝ 1．解得 x＝ ±1．
新知二 根据实际问题列二次函数表达式
根据实际问题列二次函数表达式的一般步骤1. 审清题意：找出问题中的已知量(常量)和未知量(变量)，把问题中的文字或图形语言转化成数学语言.2. 找相等关系：分析常量和变量之间的关系，列出等式.3. 列二次函数表达式：设出表示变量的字母，把相等关系用含字母的式子表示，并把它整理成二次函数的一般形式.
特别解读：1.列二次函数表达式与列一元二次方程类似;不同的是需将它转化为用含一个未知数(自变量)的代数式表示另一个未知数(函数).2.自变量的取值范围应使实际问题有意义.
某公司的生产利润原来是a 万元，经过连续两年的增长达到了y 万元，如果每年的增长率都是x，写出利润y(万元)与增长率x 之间的函数关系式，它是二次函数吗？如果是，请写出二次项系数、一次项系数和常数项.
解题秘方：基数是a万元，增长次数是2，结果为y万元，根据增长率问题的公式得出函数关系式.
解：根据题意，得y=a(1+x)2=ax2+2ax+a，是二次函数，二次项系数为a，一次项系数为2a，常数项为a.
知识储备：几种常见的二次函数关系①面积、体积的一些计算公式在特定的情况下可以看成二次函数关系式；②在特定情况下，销售利润与售价的关系；③在特定情况下，银行存款本息和与年利率的关系；④在特定情况下，总量与增长率(降低率)的关系.