苏科版6.6 图形的位似授课ppt课件

这是一份苏科版6.6 图形的位似授课ppt课件，共36页。PPT课件主要包含了学习目标，合作探究，图形的位似，归纳新知等内容，欢迎下载使用。

1.位似多边形的定义.2.位似图形的性质.3.位似图形的画法.4.平面直角坐标系中的位似.
新知一 位似多边形的定义
1. 定义如图6.6-1，两个多边形的顶点A 与A’、B 与B’、C 与C’ 所在的直线都经过同一点O，并且 = 像这样的两个多边形叫做位似多边形，点O 叫做位似中心.
2. 位似与相似的关系(1)相似仅要求两个图形的形状完全相同，而位似是在相似的基础上要求对应顶点的连线相交于一点.(2)如果两个图形是位似图形，那么这两个图形必是相似图形，但是相似的两个图形不一定是位似图形，因此, 位似是相似的特殊情况.
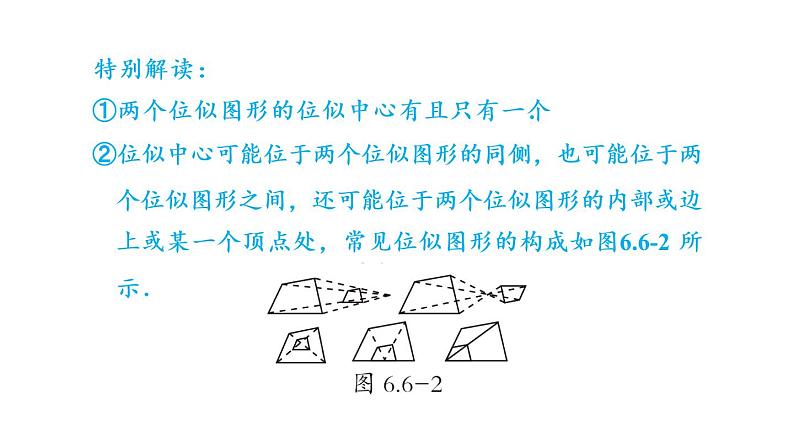
特别解读 ：①两个位似图形的位似中心有且只有一个.②位似中心可能位于两个位似图形的同侧，也可能位于两个位似图形之间，还可能位于两个位似图形的内部或边上或某一个顶点处，常见位似图形的构成如图6.6-2 所示．
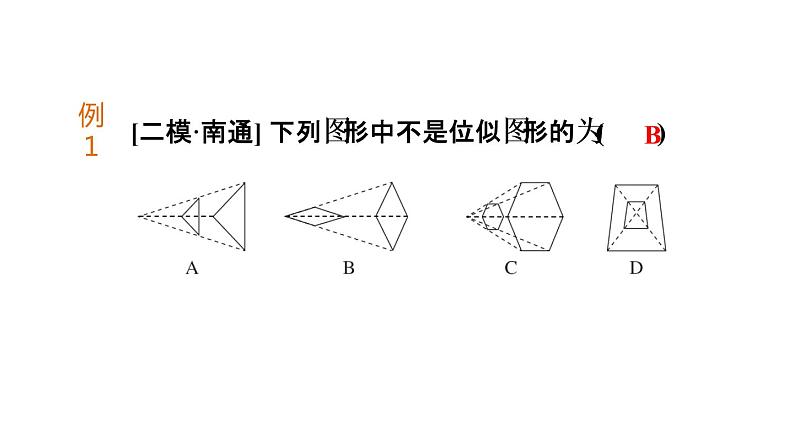
[二模·南通] 下列图形中不是位似图形的为( )
解题秘方：紧扣“位似多边形的定义”进行判断．
方法点拨：判断两个图形是否为位似图形的方法：①对应点的连线是否都经过同一点；②任意一组对应点到位似中心的距离之比是否都相等.
解：选项A、C、D 三组图形中的两个图形都是位似图形，它们的对应顶点的连线相交于一点，且任意一组对应点到位似中心的距离之比都相等；选项B 中的两个图形不符合位似多边形的定义，它们的连线虽然相交于一点，但是它们的对应顶点的连线并没有相交于一点，故不是位似图形．
新知二 位似图形的性质
位似图形具有的性质(1)位似图形每组对应顶点的连线必过位似中心.(2)位似图形任意一组对应顶点到位似中心的距离之比等于相似比.(3)位似图形的对应线段平行(或在同一条直线上)，且对应线段之比相等.(4)若两个图形位似，则这两个图形必相似，其周长比等于相似比，面积比等于相似比的平方.
示例图如图6.6-3， △ ABC与△ DEF 位似.
[模拟·无锡] 如图6.6-4，以点O 为位似中心，将△ ABC缩小后得到△ A′B′C′，已知OB=3OB′，若△ ABC 的面积为9，则△ A′B′C′的面积为 ________.
解题秘方：先求出位似比，再根据位似比等于相似比和相似三角形的面积比等于相似比的平方计算即可.
解：∵ OB=3OB′，∴ .∵以点O 为位似中心，将△ ABC 缩小后得到△ A′B′C′，∴△ A′B′C′ ∽△ ABC，∵△ ABC 的面积为9，∴△ A′B′C′ 的面积为1.
特别提醒：●位似图形是相似图形，所以它具有相似图形的一切特征.●位似与平移、轴对称、旋转一样，是图形的变化方式，但位似可以改变图形的位置和大小，其他变换只能改变图形的位置，即位似是图形的相似变换，而其他变换是图形的全等变换.
新知三 位似图形的画法
画位似图形的步骤(1)确定位似中心(位似中心可以在图形外部，也可以在图形内部，还可以在图形的边上或在某一个顶点处)；(2)分别连接位似中心和能代表原图的关键点，并延长；(3)根据相似比确定所画位似图形的关键点的位置；(4)顺次连接所作各点，得到放大或缩小的图形.
特别提醒：●位似中心的选取一般考虑要使画图方便且符合要求.●以一点为位似中心画位似图形时，符合要求的图形往往不唯一，一般情况下,同一个位似中心的两侧各有一个符合要求的图形.
[ 开放题] 如图6.6-5，已知四边形ABCD，将四边形ABCD 放大，使放大后的图形与原图形是位似图形，且放大后的图形与原图形对应线段的比为2 ∶ 1.
解题秘方：紧扣“位似图形的定义和性质”，按画位似图形的步骤作图(画法不唯一)
解：根据位似中心的不同位置情况进行作图.画法一：位似中心在四边形的顶点上，如图6.6-6，以点A为位似中心，四边形AB1C1D1就是所求作的图形.
画法二：位似中心在四边形的边上，如图6.6-7，以AD边上一点为位似中心，四边形A1B1C1D1就是所求作的图形.
另解：位似中心在四边形内部，如图6.6-8，以四边形ABCD内部一点为位似中心，四边形A1B1C1D1就是所求作的图形.
位似中心在四边形外部，如图6.6-9，以四边形ABCD外部一点为位似中心，四边形A1B1C1D1 就是所求作的图形.
新知四 平面直角坐标系中的位似
1. 位似变换时对应点的坐标变化规律一般地，在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点(x，y)对应的位似图形上的点的坐标为(kx，ky)或(－kx，－ky).
2. 位似变换与平移、轴对称、旋转三种变换的联系和区别(1)位似、平移、轴对称、旋转都是图形变换的基本形式，它们的本质区别在于：平移、轴对称、旋转三种图形变换是全等变换，而位似变换是相似变换.(2)在直角坐标系中，把一个图形进行平移、轴对称、旋转或位似变换，其对应点的坐标都有各自的变化规律：
①平移变换是横坐标或纵坐标加上(或减去)平移的距离；②在轴对称变换中，以x轴为对称轴，则对应点的横坐标相等，纵坐标互为相反数；以y轴为对称轴，则纵坐标相等，横坐标互为相反数；
③在旋转变换中，一个图形绕原点旋转180°，则旋转前后两个图形对应点的横坐标与纵坐标都分别互为相反数；④在位似变换中，当以原点为位似中心时，变换后与变换前两个图形对应点的横坐标之比的绝对值、纵坐标之比的绝对值都等于变换后的图形与变换前的图形的相似比.
特别提醒：●在平面直角坐标系中，以原点为位似中心，位似图形与原图形的相似比为k，那么当位似图形与原图形在原点的同侧时，原图形上的点(x，y)对应的位似图形上的点的坐标为(kx，ky)；当位似图形与原图形在原点的两侧时，原图形上的点(x，y)对应的位似图形上的点的坐标为(－kx，－ky).●当k＞1时，图形扩大为原来的k倍；当0＜k＜1时，图形缩小为原来的 .
如图6.6-10，已知O是坐标原点，B，C 两点的坐标分别为(3，－1)，(2，1).
解题秘方：根据位似中心及相似比作图，再利用位似变换时对应点的坐标的变化规律求对应点的坐标.
特别提醒：以原点为位似中心的位似图形的坐标变化一定要注意坐标符号的变化，简单地说，若两图形在原点同侧，则坐标符号不变，若两图形在原点异侧，则坐标符号相反.
(1)画出以点O为位似中心，在y轴的左侧将△ OBC放大为原来的2 倍(即新图与原图的相似比为2 ∶ 1)的位似图形△ OB′C′；
解：如图6.6-11，延长BO 到点B′，使OB′=2OB；延长CO 到点C′，使OC′=2OC，连接B′C′，则△ OB′C′ 就是要画的图形.
(2)分别写出B，C 两点的对应点B′，C′ 的坐标；
解：点B′，C′ 的坐标分别为(－6，2)，(－4，－2).
(3)如果△ OBC 内部一点M 的坐标为(x，y)，试写出点M 的对应点M′ 的坐标.
解：点M(x，y)的对应点M′ 的坐标为(－2x，－2y).
另解：①把点B(3，－1)，C(2，1)的横、纵坐标都乘－2，得B′(－6，2)，C′(－4，－2)；②在坐标系中描出点B′，C′；③连接OB′，B′C′，C′O，则△OB′C′就是要画的图形.