初中数学苏科版八年级下册11.3用 反比例函数解决问题多媒体教学课件ppt

这是一份初中数学苏科版八年级下册11.3用 反比例函数解决问题多媒体教学课件ppt，共14页。PPT课件主要包含了情境导入，本课学习要点，你学会了吗，拓展与延伸等内容，欢迎下载使用。

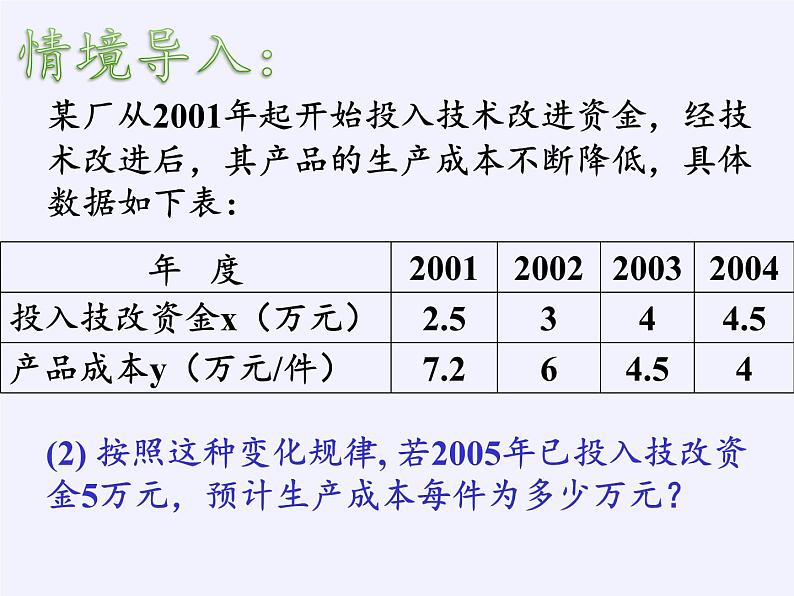
某厂从2001年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：
(2) 按照这种变化规律, 若2005年已投入技改资金5万元，预计生产成本每件为多少万元？
11.3 用反比例函数解决问题（1）
能利用反比例函数的相关知识分析和解决一些简单的实际问题。
（3）小明希望能在2 h内完成录入任务，那么他每分钟至少应录入多少字？
问题1、小明将一篇7500字的论文录入电脑，打印成文。
（1）完成录入任务的时间t(min)与录入文字的速度v（字/min）有怎样的函数关系？
（2）如果小明以每分钟100字的速度录入，他需要多长时间才能完成录入任务？
练习：A、B两地相距300 km，汽车以 x km/h的速度从A地到达B地需要 y h，（1）写出 y 与 x 的函数表达式。（2）如果汽车的速度不超过100 km/h，那么汽车从A地到B地至少需要多少时间？
问题2、某自来水公司计划新建一个容积为3×104 m3的长方体蓄水池。（1）蓄水池的底面积S（m2）与其深度h(m)有怎样的函数关系？
（2）如果蓄水池的深度设计为 6 m，那么蓄水池的底面积应为多少 m2 ？
（3）由于绿化以及辅助用地的需要，经过实地测量，蓄水池的长和宽最多只能设计为80m和60m，那么蓄水池的深度至少达到多少才能满足要求。
练习：市煤气公司要在地下修建一个容积为 104 m3的圆柱形煤气储存室.(1)储存室的底面积 S(m2)与其深度d (m)有怎样的函数关系?(2)公司决定把储存室的底面积S定为500 m2,施工队施工时应该向下掘进多深?(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?
①要注意自变量取值范围符合实际意义;②确定反比例函数之前一定要考察两个变量与定值之间的关系;若k未知时应首先由已知条件求出k值.③求“至少,最多”时可先求关键点，再根据函数性质得到.
▲应用反比例函数解决实际问题时的注意点。
为了预防流感,某学校对教室采用药熏消毒法进行消毒, 已知药物燃烧时,室内每立方
6 mg,请根据题中所提供的信息,解答下列问题:
米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为
(1)分别求出药物燃烧时和药物燃烧后，y关于x的函数关系式以及自变量的取值范围。
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室？
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?