





还剩26页未读,
继续阅读
11.1 与三角形有关的线段课件PPT
展开
这是一份11.1 与三角形有关的线段课件PPT,共34页。
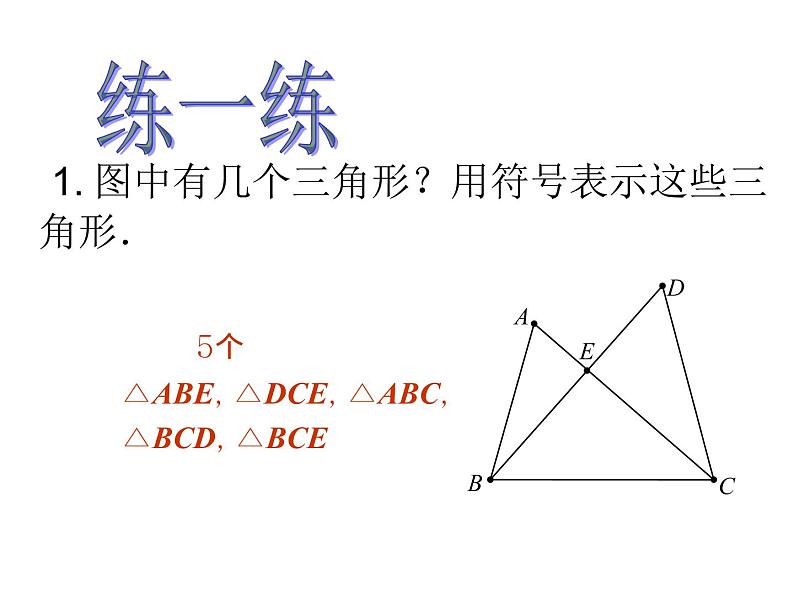
1金字塔分子结构香港中银大厦你能从中找到自己熟悉的图形吗? 2★ 你所了解的三角形有些什么特点呢? ?★ 你能根据自己的观察,给三角形下一个定义吗?观察思考3 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形. 认识新知4认识新知 如图所示,线段AB,BC,CA是三角形的边. 点A,B,C是三角形的顶点. ∠A, ∠B, ∠C, 是相邻两边组成的角,叫做三角形的内角,简称三角形的角.顶点是A,B,C的三角形,记作“△ABC”.cbaCBA5 1. 图中有几个三角形?用符号表示这些三角形. 5个 △ABE, △DCE, △ABC, △BCD, △BCE练一练6 如图,按要求完成下列填空.(1)用符号表示图中的三角形 ;(2)以BD为边的三角形有 ;(3)以点A为一个顶点的三角形有 ;(4)以∠C为一个内角的三角形有 .练一练△ABD,△BCD,△ABC △ABD,△BCD △ABD,△ABC △BCD,△ABC 7探究图上的三角形分别有怎样的特点呢?它属于哪一种三角形呢? 8归纳【按三个内角大小分】三角形锐角三角形直角三角形钝角三角形【按边的相等关系分】三角形不等边三角形等腰三角形底边和腰不相等的等腰三角形等边三角形9即: 任意画一个△ABC,假设一只小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?动手实践,探索新知三角形两边的和大于第三边10 下列长度的三条线段能否组成三角形?为什么?(1)3,4,8;(2)5,6,11;(3)5,6,10.巩固新知不能不能能11巩固应用,深入理解 【例】用一条长为18cm的细绳围成一个等腰三角形.(1)如果腰长是底边的2倍,那么各边的长是多少?(2)能围成有一边的长为4cm的等腰三角形吗?为什么?12补充练习 已知一个三角形的两边长分别为2cm和13cm,若该三角形的周长为奇数,则第三边长为多少? 答案:12cm或14cm 13还记得吗? (1)过一点画已知直线的垂线?(2)如何画线段AB的中点? (3)如何画∠ACB的角平分线? 14想一想:过三角形的一个顶点,你能画出它的对边的垂线吗? 15 如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.用同样的方法,你能画出△ABC的另两条边上的高吗?根据你的观察,三角形的三条高交于几个点呢?三角形的三条高交于一个点.DEF16 【巩固练习】 你能分别画出直角三角形和钝角三角形的三条高吗? 画钝角三角形的三条高时,有两个垂足落在边的延长线上. DEFD17 你能根据自己的观察,画出△ABC的一条中线吗?连接△ABC的顶点和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线. D18【练习】 用同样的方法,你能画出△ABC的另两条边上的中线吗?根据你的观察,三角形的三条中线交于几个点呢?三角形的三条中线交于一点. EF19【巩固练习】 你能分别画出直角三角形和钝角三角形的三条中线吗?任意三角形的三条中线都在三角形的内部.FFDEDE20 你能根据自己的观察,画出三角形的一条角平分线吗? 画∠A的平分线AD,交所对的边BC于点D,所得线段AD叫做△ABC的角平分线. D21 用同样的方法,你能画出△ABC的另两条角平分线吗?根据你的观察,三角形的三条角平分线交于几个点呢?三角形的三条角平分线交于一个点.FE22【巩固练习】 你能分别画出直角三角形和钝角三角形的三条角平分线吗?任意三角形的三条角平分线都在三角形的内部 .FDEDEF23应用新知,巩固提升如图,(1)(2)和(3)中的三个∠B有什么不同?这三个△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗? (1)(2)(3)24应用新知,巩固提升(1)如图(1),AD,BE,CF是△ABC的三条中线,则AB=2 ,BD= ,AE=1/2 .(2)如图(2),AD,BE,CF是△ABC的三条角平分线,则∠1= , ∠3 =1/2 ,∠ACB=2 .(1)(2)AFCDAC∠4∠ABC∠225应用新知,巩固提升【巩固练习】如图,在△ABC中,AB=2cm,BC=4cm,△ABC的高AD与CE的比是多少?(提示:利用三角形的面积公式)26应用新知,巩固提升【巩固练习】如图,AD是△ABC的角平分线,DE∥AC,DE交AB于E,DF∥AB,DF交AC于F.图中∠1与∠2有什么关系?为什么?27知识延伸,生活链接 盖房子时,在窗框未安装好之前,木工师傅常常现在窗框上斜钉一根木条.为什么要这样做? 三角形具有稳定性,四边形不具有稳定性.28思考:如图(1),将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?如图(2),将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?如图(3),在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?29练一练:下列图形中哪些具有稳定性?√√√×××30拓展练习: 三角形的稳定性有广泛的应用,你能再举一些例子吗?31想一想: 要使四边形木架(用4根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?32归纳总结,布置作业这节课,你有什么收获? 作业:第1题;质量监测同步练习. 33同学们再见!34
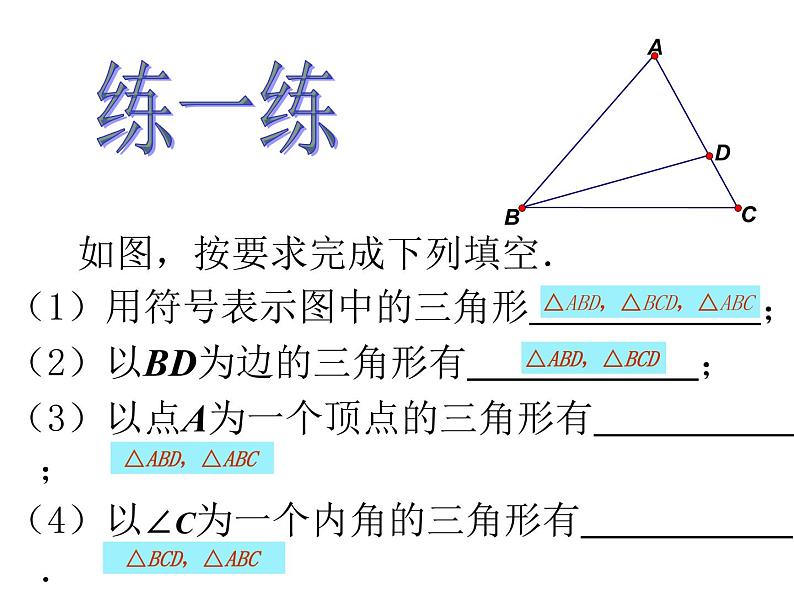
1金字塔分子结构香港中银大厦你能从中找到自己熟悉的图形吗? 2★ 你所了解的三角形有些什么特点呢? ?★ 你能根据自己的观察,给三角形下一个定义吗?观察思考3 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形. 认识新知4认识新知 如图所示,线段AB,BC,CA是三角形的边. 点A,B,C是三角形的顶点. ∠A, ∠B, ∠C, 是相邻两边组成的角,叫做三角形的内角,简称三角形的角.顶点是A,B,C的三角形,记作“△ABC”.cbaCBA5 1. 图中有几个三角形?用符号表示这些三角形. 5个 △ABE, △DCE, △ABC, △BCD, △BCE练一练6 如图,按要求完成下列填空.(1)用符号表示图中的三角形 ;(2)以BD为边的三角形有 ;(3)以点A为一个顶点的三角形有 ;(4)以∠C为一个内角的三角形有 .练一练△ABD,△BCD,△ABC △ABD,△BCD △ABD,△ABC △BCD,△ABC 7探究图上的三角形分别有怎样的特点呢?它属于哪一种三角形呢? 8归纳【按三个内角大小分】三角形锐角三角形直角三角形钝角三角形【按边的相等关系分】三角形不等边三角形等腰三角形底边和腰不相等的等腰三角形等边三角形9即: 任意画一个△ABC,假设一只小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?动手实践,探索新知三角形两边的和大于第三边10 下列长度的三条线段能否组成三角形?为什么?(1)3,4,8;(2)5,6,11;(3)5,6,10.巩固新知不能不能能11巩固应用,深入理解 【例】用一条长为18cm的细绳围成一个等腰三角形.(1)如果腰长是底边的2倍,那么各边的长是多少?(2)能围成有一边的长为4cm的等腰三角形吗?为什么?12补充练习 已知一个三角形的两边长分别为2cm和13cm,若该三角形的周长为奇数,则第三边长为多少? 答案:12cm或14cm 13还记得吗? (1)过一点画已知直线的垂线?(2)如何画线段AB的中点? (3)如何画∠ACB的角平分线? 14想一想:过三角形的一个顶点,你能画出它的对边的垂线吗? 15 如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.用同样的方法,你能画出△ABC的另两条边上的高吗?根据你的观察,三角形的三条高交于几个点呢?三角形的三条高交于一个点.DEF16 【巩固练习】 你能分别画出直角三角形和钝角三角形的三条高吗? 画钝角三角形的三条高时,有两个垂足落在边的延长线上. DEFD17 你能根据自己的观察,画出△ABC的一条中线吗?连接△ABC的顶点和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线. D18【练习】 用同样的方法,你能画出△ABC的另两条边上的中线吗?根据你的观察,三角形的三条中线交于几个点呢?三角形的三条中线交于一点. EF19【巩固练习】 你能分别画出直角三角形和钝角三角形的三条中线吗?任意三角形的三条中线都在三角形的内部.FFDEDE20 你能根据自己的观察,画出三角形的一条角平分线吗? 画∠A的平分线AD,交所对的边BC于点D,所得线段AD叫做△ABC的角平分线. D21 用同样的方法,你能画出△ABC的另两条角平分线吗?根据你的观察,三角形的三条角平分线交于几个点呢?三角形的三条角平分线交于一个点.FE22【巩固练习】 你能分别画出直角三角形和钝角三角形的三条角平分线吗?任意三角形的三条角平分线都在三角形的内部 .FDEDEF23应用新知,巩固提升如图,(1)(2)和(3)中的三个∠B有什么不同?这三个△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗? (1)(2)(3)24应用新知,巩固提升(1)如图(1),AD,BE,CF是△ABC的三条中线,则AB=2 ,BD= ,AE=1/2 .(2)如图(2),AD,BE,CF是△ABC的三条角平分线,则∠1= , ∠3 =1/2 ,∠ACB=2 .(1)(2)AFCDAC∠4∠ABC∠225应用新知,巩固提升【巩固练习】如图,在△ABC中,AB=2cm,BC=4cm,△ABC的高AD与CE的比是多少?(提示:利用三角形的面积公式)26应用新知,巩固提升【巩固练习】如图,AD是△ABC的角平分线,DE∥AC,DE交AB于E,DF∥AB,DF交AC于F.图中∠1与∠2有什么关系?为什么?27知识延伸,生活链接 盖房子时,在窗框未安装好之前,木工师傅常常现在窗框上斜钉一根木条.为什么要这样做? 三角形具有稳定性,四边形不具有稳定性.28思考:如图(1),将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?如图(2),将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?如图(3),在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?29练一练:下列图形中哪些具有稳定性?√√√×××30拓展练习: 三角形的稳定性有广泛的应用,你能再举一些例子吗?31想一想: 要使四边形木架(用4根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?32归纳总结,布置作业这节课,你有什么收获? 作业:第1题;质量监测同步练习. 33同学们再见!34
相关资料
更多









