




还剩9页未读,
继续阅读
初中数学人教 版八年级下册 数学活动7 课件
展开
这是一份初中数学人教 版八年级下册 数学活动7 课件,共17页。
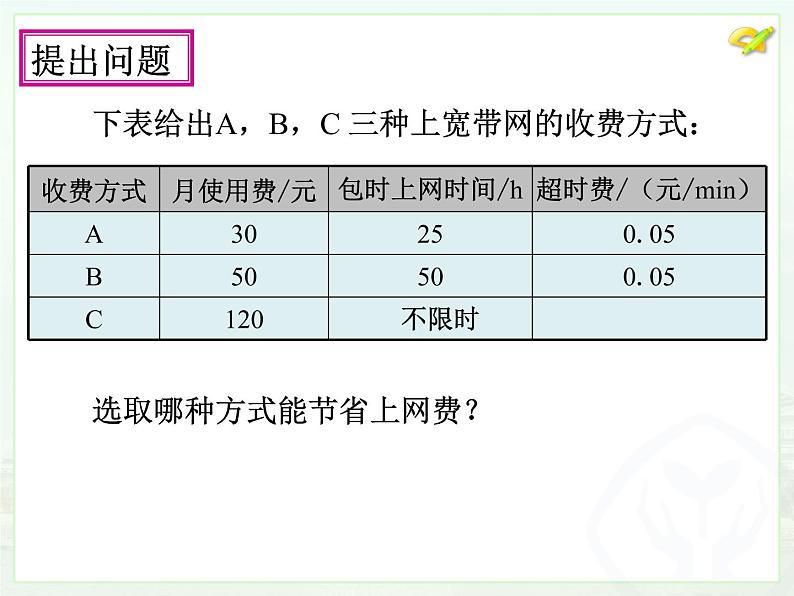
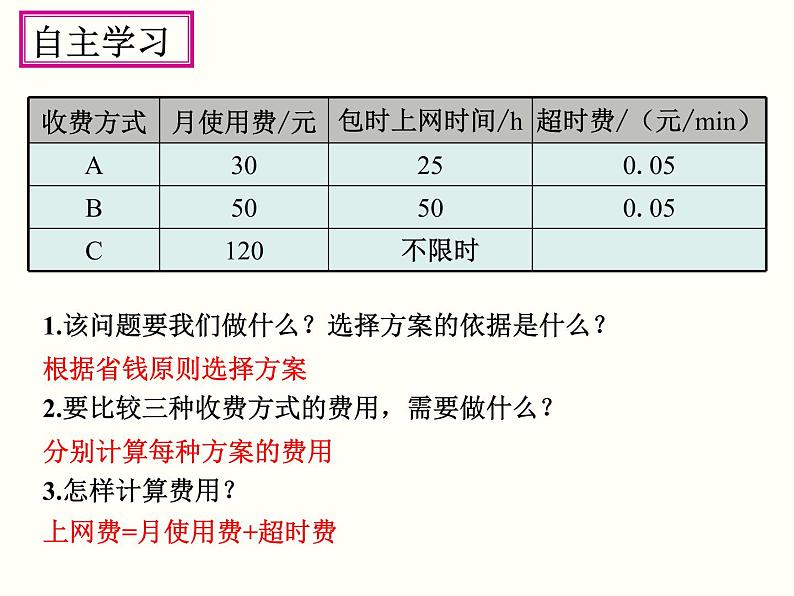
导入新课自主学习合作探究交流展示19.3 课题学习 选择方案第十九章 一次函数巩固拓展学习目标: 1.会用一次函数知识解决方案选择问题,体会函数 模型思想; 2.能从不同的角度思考问题,优化解决问题的方法; 3.能进行解决问题过程的反思,总结解决问题的方 法.学习重点: 建立函数模型解决方案选择问题.课件说明 某人名白日梦,某日向某公司老板求职,老板答应他:试用一周(七天)日工资20元。白日梦对老板说:“日工资是否再谈一谈?”老板很随和地说:“你开个价吧。”白日梦心中暗喜地说:“第一天你付给我5分,第二天付给我25分,以后每天付给我的钱是前一天与第一天钱数的积。”老板听了,略加思考后与白日梦签下了合同。 签完合同后,白日梦高兴得手舞足蹈,沾沾自喜地盘算着: 第一天:5分;第二天:25分;第三天:25×5=53=125分…… 第六天:56=15625分=156.25元;第七天:57=78125分=781.25元。 一 周=5+25+-----+15625+78125=97655分=976.55元。 签完合同后,老板更是美不胜收,心想: 第一天:0.05元;第二天:0.25元; 第三天:0.25 × 0.05=0.0125元……情景导入想一想: 做一件事情,有时有不同的实施方案.你怎样从中选择最佳方案呢?情景导入 做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常必要的.在选择方案时,往往需要从数学的角度分析,涉及变量的问题常用到函数. 下表给出A,B,C 三种上宽带网的收费方式: 选取哪种方式能节省上网费? 提出问题1.该问题要我们做什么?选择方案的依据是什么?根据省钱原则选择方案2.要比较三种收费方式的费用,需要做什么?分别计算每种方案的费用3.怎样计算费用?上网费=月使用费+超时费自主学习4.A,B,C 三种方案中,所需要的费用是固定的还是变化的? 方案C费用固定; 方案A,B的费用在超过一定时间后,随上网时间变化,是上网时间的函数.自主学习5.请分别写出三种方案的上网费用y 元与上网时间x h之间的函数解析式.在方式A中,超时费一定会产生吗?什么情况下才会有超时费?超时费不是一定有的,只有在上网时间超过25h时才会产生.上网费=月使用费+超时费合起来可写为:当0≤x≤25时,y1=30;当x>25时,y1=30+0.05×60(x-25)=3x-45.你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗?方式C的上网费y3关于上网时间x之间的函数关系式呢?当x≥0时,y3=120. 你能把这个问题描述为函数问题吗? 能把这个问题描述为函数问题吗? 设上网时间为x,方案A,B,C的上网费用分别为y1 元,y2 元, y3 元,且分析问题请比较y1,y2,y3的大小. 这个问题看起来还是有点复杂,难点在于每一个函数的解析都是分类表示的,需要分类讨论,而怎样分类是难点.怎么办? ——先画出图象看看.y3=120. 当上网时间__________时,选择方式A最省钱.当上网时间__________时,选择方式B最省钱.当上网时间_________时,选择方式C最省钱.这个实际问题的解决过程中是怎样思考的?实际问题设变量找对应关系一次函数问题一次函数问题的解实际问题的解解释实际意义知识要点 1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.>1500巩固拓展 2.为更新果树品种,某果园计划新购进A,B两个苹果的果树树苗栽植培育,若计划购进这两种果树树苗共45棵,其中A树苗的单价为7元/棵,购进B树苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系,(1)求y与x的函数关系式;(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A中苗的数量,请设计购买方案,使总费用最低,并求出最低费用.巩固拓展 3. 某移动公司对于移动话费推出两种收费方式: A方案:每月收取基本月租费15元,另收通话费 为0.2元/min; B方案: 零月租费,通话费为0.3元/min. (1)试写出A,B两种方案所付话费y(元)与通话 时间t(min)之间的函数关系式;(2)在同一坐标系画出这两个函数的图象,并指出那 种付费方式合算?巩固拓展(2)这两个函数的图象如下:t(min)y = 15+0.2ty = 0.3t观察图象,可知:当t=150min时,选择A或B方案费用一样;当0150min时,选择A方案合算.课堂小结解决方案问题步骤:1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).2.通过解不等式或列表的方式确定自变量的范围.3.利用一次函数的增减性知识从而选择出最佳方案.
导入新课自主学习合作探究交流展示19.3 课题学习 选择方案第十九章 一次函数巩固拓展学习目标: 1.会用一次函数知识解决方案选择问题,体会函数 模型思想; 2.能从不同的角度思考问题,优化解决问题的方法; 3.能进行解决问题过程的反思,总结解决问题的方 法.学习重点: 建立函数模型解决方案选择问题.课件说明 某人名白日梦,某日向某公司老板求职,老板答应他:试用一周(七天)日工资20元。白日梦对老板说:“日工资是否再谈一谈?”老板很随和地说:“你开个价吧。”白日梦心中暗喜地说:“第一天你付给我5分,第二天付给我25分,以后每天付给我的钱是前一天与第一天钱数的积。”老板听了,略加思考后与白日梦签下了合同。 签完合同后,白日梦高兴得手舞足蹈,沾沾自喜地盘算着: 第一天:5分;第二天:25分;第三天:25×5=53=125分…… 第六天:56=15625分=156.25元;第七天:57=78125分=781.25元。 一 周=5+25+-----+15625+78125=97655分=976.55元。 签完合同后,老板更是美不胜收,心想: 第一天:0.05元;第二天:0.25元; 第三天:0.25 × 0.05=0.0125元……情景导入想一想: 做一件事情,有时有不同的实施方案.你怎样从中选择最佳方案呢?情景导入 做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常必要的.在选择方案时,往往需要从数学的角度分析,涉及变量的问题常用到函数. 下表给出A,B,C 三种上宽带网的收费方式: 选取哪种方式能节省上网费? 提出问题1.该问题要我们做什么?选择方案的依据是什么?根据省钱原则选择方案2.要比较三种收费方式的费用,需要做什么?分别计算每种方案的费用3.怎样计算费用?上网费=月使用费+超时费自主学习4.A,B,C 三种方案中,所需要的费用是固定的还是变化的? 方案C费用固定; 方案A,B的费用在超过一定时间后,随上网时间变化,是上网时间的函数.自主学习5.请分别写出三种方案的上网费用y 元与上网时间x h之间的函数解析式.在方式A中,超时费一定会产生吗?什么情况下才会有超时费?超时费不是一定有的,只有在上网时间超过25h时才会产生.上网费=月使用费+超时费合起来可写为:当0≤x≤25时,y1=30;当x>25时,y1=30+0.05×60(x-25)=3x-45.你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗?方式C的上网费y3关于上网时间x之间的函数关系式呢?当x≥0时,y3=120. 你能把这个问题描述为函数问题吗? 能把这个问题描述为函数问题吗? 设上网时间为x,方案A,B,C的上网费用分别为y1 元,y2 元, y3 元,且分析问题请比较y1,y2,y3的大小. 这个问题看起来还是有点复杂,难点在于每一个函数的解析都是分类表示的,需要分类讨论,而怎样分类是难点.怎么办? ——先画出图象看看.y3=120. 当上网时间__________时,选择方式A最省钱.当上网时间__________时,选择方式B最省钱.当上网时间_________时,选择方式C最省钱.这个实际问题的解决过程中是怎样思考的?实际问题设变量找对应关系一次函数问题一次函数问题的解实际问题的解解释实际意义知识要点 1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.>1500巩固拓展 2.为更新果树品种,某果园计划新购进A,B两个苹果的果树树苗栽植培育,若计划购进这两种果树树苗共45棵,其中A树苗的单价为7元/棵,购进B树苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系,(1)求y与x的函数关系式;(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A中苗的数量,请设计购买方案,使总费用最低,并求出最低费用.巩固拓展 3. 某移动公司对于移动话费推出两种收费方式: A方案:每月收取基本月租费15元,另收通话费 为0.2元/min; B方案: 零月租费,通话费为0.3元/min. (1)试写出A,B两种方案所付话费y(元)与通话 时间t(min)之间的函数关系式;(2)在同一坐标系画出这两个函数的图象,并指出那 种付费方式合算?巩固拓展(2)这两个函数的图象如下:t(min)y = 15+0.2ty = 0.3t观察图象,可知:当t=150min时,选择A或B方案费用一样;当0
相关课件
初中数学人教 版八年级下册 数学活动10 课件: 这是一份初中数学人教 版八年级下册 数学活动10 课件,共9页。
初中数学人教 版八年级下册 数学活动1 课件: 这是一份初中数学人教 版八年级下册 数学活动1 课件,共7页。
初中数学人教 版八年级下册 数学活动2 课件: 这是一份初中数学人教 版八年级下册 数学活动2 课件,共24页。













