初中数学人教 版八年级下册 特殊平行四边形性质判定综合应用 课件

这是一份初中数学人教 版八年级下册 特殊平行四边形性质判定综合应用 课件，共10页。

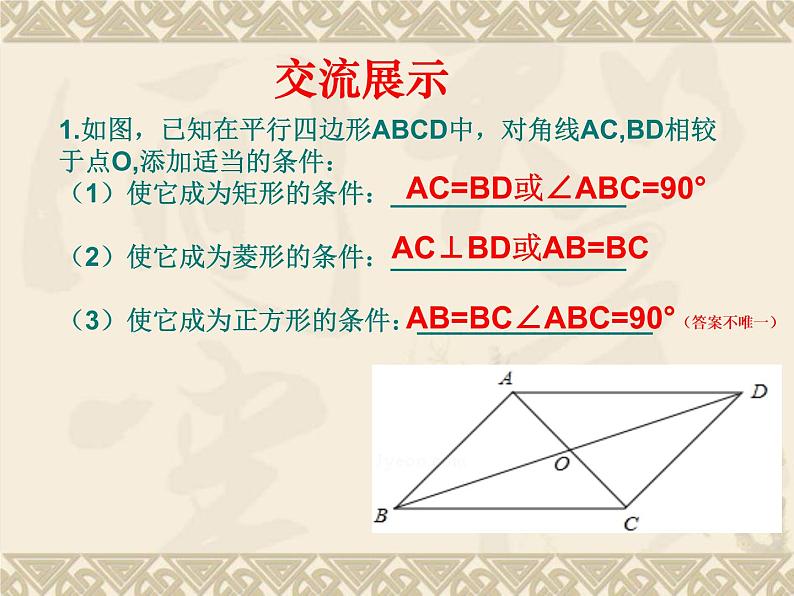
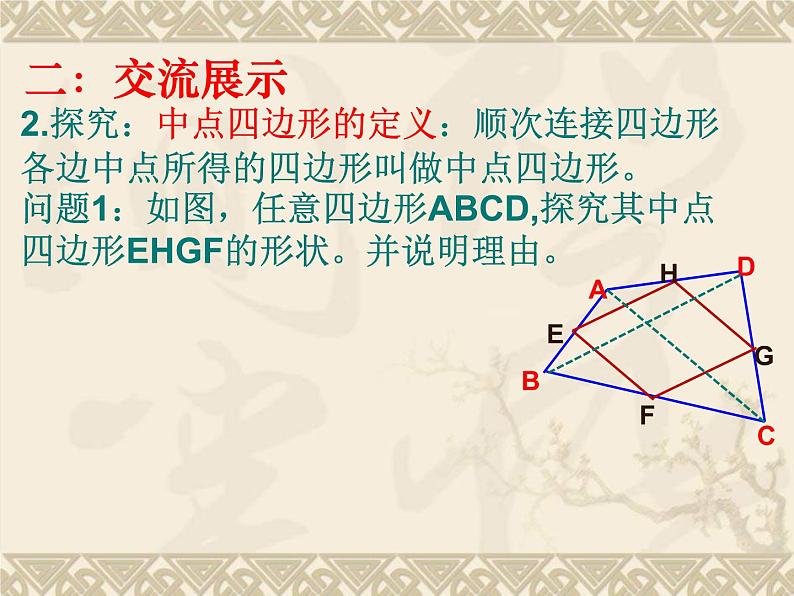
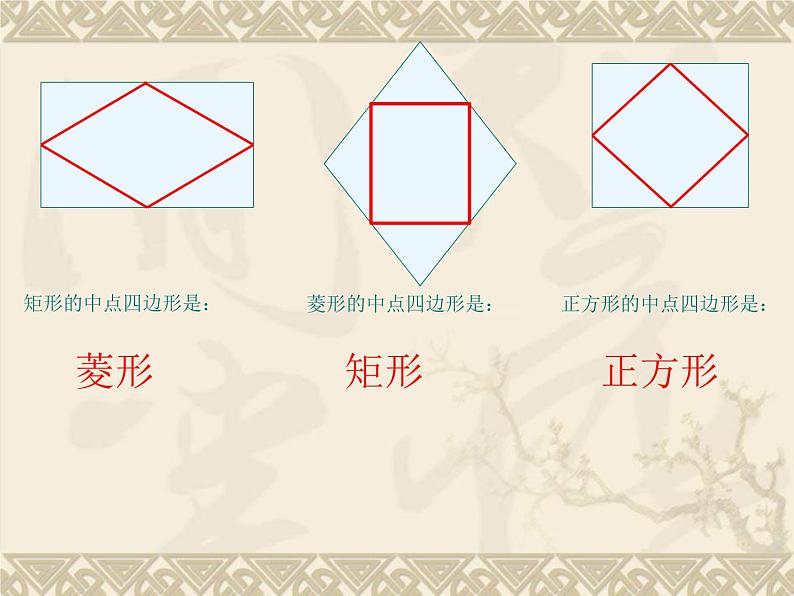
人教版八年级下册特殊平行四边形复习江陵县熊河中学 陈航自主学习我参与，我成功，我快乐，我们是课堂的主人交流展示1.如图，已知在平行四边形ABCD中，对角线AC,BD相较于点O,添加适当的条件：（1）使它成为矩形的条件：________________（2）使它成为菱形的条件：________________（3）使它成为正方形的条件：________________AC⊥BD或AB=BCAC=BD或∠ABC=90°AB=BC∠ABC=90°（答案不唯一）2.探究：中点四边形的定义：顺次连接四边形各边中点所得的四边形叫做中点四边形。问题1：如图，任意四边形ABCD,探究其中点四边形EHGF的形状。并说明理由。二：交流展示菱形矩形正方形矩形的中点四边形是：菱形的中点四边形是：正方形的中点四边形是：ABCDEFGHABCD结论：任意四边形的中点四边形是________________；中点四边形的形状与原四边形的 ______密切相关 对角线（1）当原四边形的对角线相等时，中点四边形是______； （2）当原四边形的对角线垂直时，中点四边形 ______；（3）当原四边形的对角线互相垂直且相等时，中点四边形是_________。菱形正方形矩形二：交流展示平行四边形1.如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．（1）求证：CE=AD；（2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；三：反馈评价（1）证明：∵DE⊥BC，∴∠DFB=90°，∵∠ACB=90°，∴∠ACB=∠DFB，∴AC∥DE，∵MN∥AB，即CE∥AD，∴四边形ADEC是平行四边形，∴CE=AD；（2）解：四边形BECD是菱形，理由是：∵D为AB中点，∴AD=BD，∵CE=AD，∴BD=CE，∵BD∥CE，∴四边形BECD是平行四边形，∵∠ACB=90°，D为AB中点，∴CD=BD，∴四边形BECD是菱形；四：评价小结和大家分享下你本节课的收获。五：课后作业在“反馈练习”的基础上增加第3问： （3）当∠A的大小满足什么条件时，四边形BECD 是正方形？请说明你的理由。