



2021学年1 平行线授课课件ppt
展开1.在丰富的现实情境中,进一步了解两条平行线的位置关系,掌握有关的符号表示.2.会用三角尺、量角器、方格纸画平行线,积累操作活动的经验.3.在操作活动中,探索并了解平行线的有关性质.
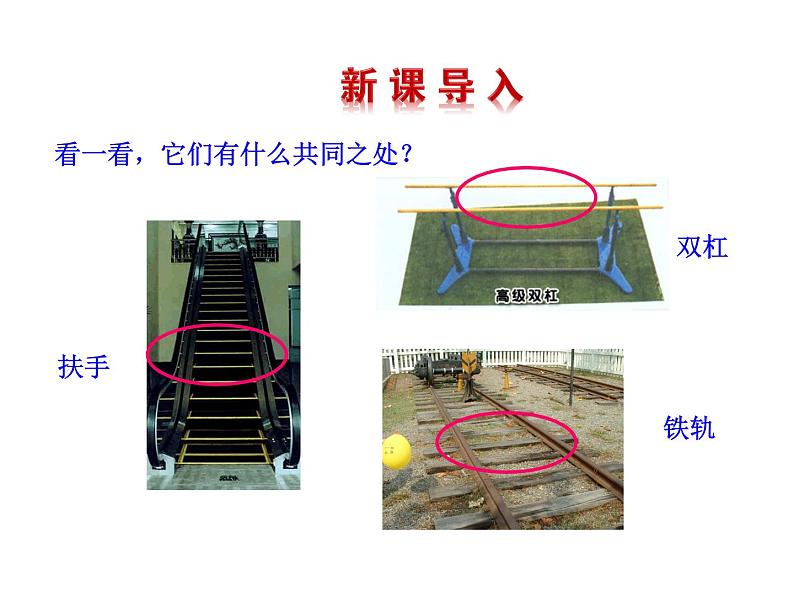
看一看,它们有什么共同之处?
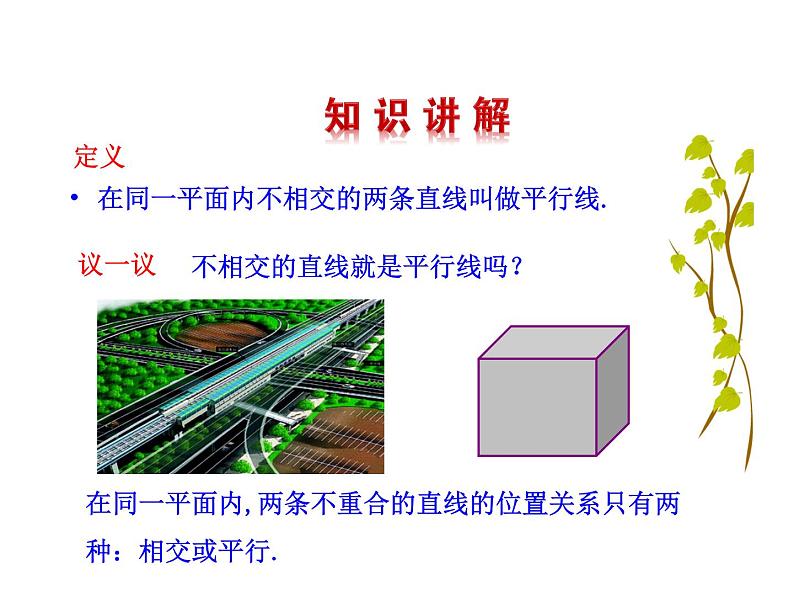
在同一平面内不相交的两条直线叫做平行线.
不相交的直线就是平行线吗?
在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行.
找一找,图中有哪些平行线?
1.自动扶梯的左、右扶手如果不平行会出现什么情况?
2.铁路的铁轨如果不平行,又会出现什么情况?
你能在方格纸上画出平行线吗?有几种画法?
你能借助三角尺画出平行线吗?
(一落,二靠,三移,四画)
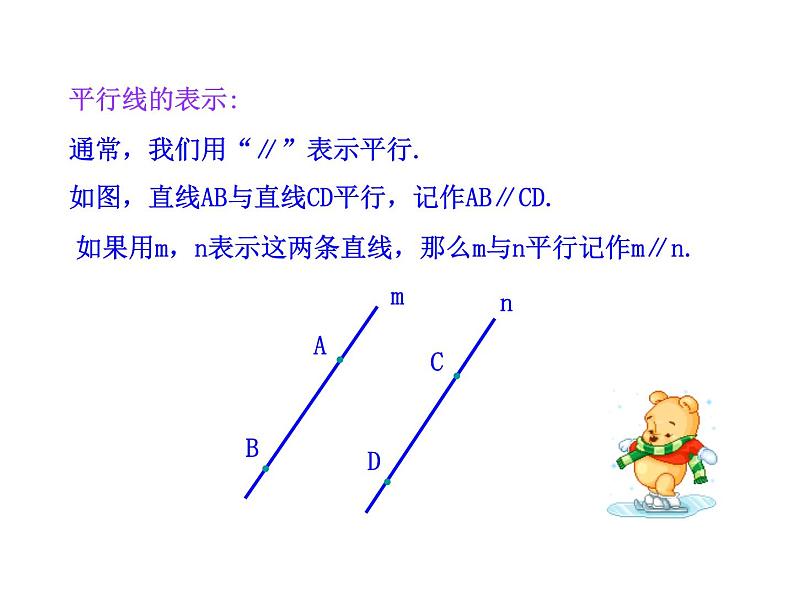
通常,我们用“∥”表示平行.
如图,直线AB与直线CD平行,记作AB∥CD.
如果用m,n表示这两条直线,那么m与n平行记作m∥n.
如图,直线AB外有两点P,Q.(1)你能过点P画一条直线与直线AB平行吗?
这样的直线还能画吗?
(2)再过点Q画一条直线与直线AB平行.
它与前面所画的直线平行吗?
通过画图,你发现了什么?
性质1:过直线外一点有且只有一条直线与这条直线平行.
性质2:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
【例1】在同一平面内有四条直线a,b,c,d,已知:a∥d,b∥c,b∥d,则a和c的位置关系是 .
【解析】因为a∥d,b∥d,所以a∥b,又因为b∥c,所以a∥c.
1.在同一平面内,不重合的两条直线的位置关系是: .
2.下列说法正确的是( )A.在同一平面内,两条不平行的线段必相交B.在同一平面内,不相交的两条线段是平行线C.两条射线或线段平行,是指它们所在的直线平行D.以上说法均不正确
3.在同一平面内有三条直线,若有且只有两条平行,那么这三条直线的交点数为( )A.0个 B.1个 C.2个 D.3个
4.三条直线AB,CD,EF,若AB‖EF,CD‖EF,则 ‖ ,理由是_____________________
1.如图所示,(1)过点C能画出几条与直线AB平行的直线?(2)过点D与直线AB平行的直线,与(1)中所画的直线平行吗?(3)由(2)你发现了什么结论?
答案:(1)一条.(2)平行.(3)如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
2.在同一平面内的两条直线a和b,分别根据下列条件,写出a,b的位置关系.(1)如果它们没有公共点,则 .(2)如果它们都平行于第三条直线,则 .(3)如果它们有且只有一个公共点,则 .(4)过平面内的同一点画它们的平行线,能画出两条,则 .(5)过平面内的不在a,b上的一点画它们的平行线,只能画出一条,则 .
3.在下列4个说法中正确的有 .①在同一平面内,不相交也不重合的两条线段一定平行;②在同一平面内, 不相交也不重合的两条直线一定平行;③在同一平面内,不平行也不重合的两条线段一定相交;④在同一平面内,不平行也不重合的两条直线一定相交.
【解析】平行线概念中强调的是“两条直线”而不是线段或射线.两条线段平行是指两条线段所在的直线平行.
4.在同一平面内,两条相交直线公共点的个数是______;两条平行直线的公共点的个数是_____;两条直线重合,公共点有_________.
1.平行线的定义.2.生活中充满了“平行”.3.画平行线的方法. 4.平行线的表示. 5.平行线的性质.
对人以诚信,人不欺我;对事以诚信,事无不成.
1.掌握平行线的判定方法.2.能应用平行线的判定方法判定两直线平行.3.能进行简单的逻辑推理,提高对数学符号的认 识,发展逻辑推理能力.
1.同一个平面内的两条直线的位置关系有哪几种?
2.怎样的两条直线平行?
在画图过程中,三角板起到什么作用?要判断直线a‖b,你有办法吗?
①如图:如果∠1=∠2,那么a与b平行吗?∵ ____=____(已知),∴ __∥__(同位角相等,两直线平行).
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单地说:同位角相等,两直线平行.
② 如图:如果∠1=∠2, 那么a与b平行吗?
内错角相等,两直线平行.
∵ ____=____(已知),∴ ___∥___(内错角相等,两直线平行).
③ 如图:如果∠1+∠2=180°,那么a与b平行吗?
同旁内角互补,两直线平行.
∵ ____+____=180°(已知),∴ ___∥___(同旁内角互补,两直线平行).
④ 如图:如果a⊥l,b⊥l 那么a与b平行吗?
∵ __⊥__,__⊥__ (已知),∴ ___∥___(在同一平面内,垂直于同一直线的两直线平行).
在同一平面内,垂直于同一条直线的两条直线平行.
a l b l
同位角相等,两直线平行.
直线平行的条件
【例】 如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?
解析:由已知条件可得∠B+∠C = 180°.根据同旁内角互补,两直线平行,可知AB∥CD.但根据题目的已知条件,无法判定AD与BC平行.
① ∵ ∠2 = (已知), ∴ ___∥___
② ∵ ∠3 = (已知), ∴ ___∥___
③ ∵ ∠4 + =180°(已知), ∴ ___∥___
(同位角相等,两直线平行).
(内错角相等,两直线平行).
(同旁内角互补,两直线平行).
2.如图:已知 ∠1=75° , ∠2 =105°问:直线AB与CD平行吗?为什么?
解析:直线AB与CD平行.因为∠1= 75°,所以 ∠3=180°-75°=105°.又因为∠2 =105°,所以 ∠3 =∠2.所以 AB∥CD(同位角相等,两直线平行).
试用其他方法说明直线AB与CD平行.
1.如图,如果∠B=∠1,则可得_______∥_______;根据是________________________.如果∠D=∠1,则可得到_______∥_______;根据是________________________.
同位角相等,两直线平行
内错角相等,两直线平行
(1) ∵ ∠1 = _____(已知), ∴ AB∥CE
(2) ∵ ∠1 + _____=180°(已知), ∴ CD∥BF
(3) ∵ ∠1 +∠5 =180°(已知), ∴ _____∥_____
(4) ∵ ∠4 +_____=180°(已知), ∴ CE∥AB
3.如图,直线a,b被c所截,已知∠1=120°,∠2=60°,直线a与b平行吗?为什么?
解析:a与b平行.∵∠1=∠3(对顶角相等),∠1=120°(已知),∴∠3=120°.∵∠2=60°,∴∠2+∠3=180°,∴a∥b(同旁内角互补,两直线平行).
4.已知∠3=45°,∠1与∠2互余,试说明AB∥CD?
解析:由于∠1与∠2是对顶角,∴∠1=∠2.又∵∠1+∠2=90°(已知),∴∠1=∠2=45°.∵∠3=45°(已知),∴∠2=∠3.∴ AB∥CD(内错角相等,两直线平行).
风再冷,不会永远不息;雾再浓,不会经久不散.风息雾散,仍是阳光灿烂.
1.掌握平行线的性质.2.能应用平行线的性质计算角度或辨别角之间的关系.3.能综合运用平行线的性质与判定进行简单的推理,提高对几何语言的认识,发展逻辑推理能力.
问题1: 如图一束平行光线AB和DE射向一个水平镜面后被反射,此时∠1,∠3的大小有什么关系?
问题2:当两人目光相对时,视线与水平方向的夹角∠1与∠2相等吗?
探索:两直线平行,同位角有什么关系?
探索:两直线平行,内错角、同旁内角又有什么关系?
活动要求:①利用坐标纸上的直线或者用直尺和三角尺画两条平行线a,b,然后,画一条截线c与这两条平行线相交,标出如图的角;
(1)探索:两直线平行,同位角有什么关系?
②度量这些角,把结果填入下表;③你发现各对同位角的度数之间有什么关系?写出你的猜想.
再任意画一条截线d, 同样度量并计算各个角的度数,你的猜想还成立吗?(要求学生多画几条截线来验证)
(2)验证“两直线平行,同位角相等”
(3)问题:如果直线a与b不平行,你的猜想还成立吗?
结论:如果直线a与b不平行, 同位角则不相等.
一般地,平行线具有的性质:性质1 两条平行线被第三条直线所截,同位角相等.以上性质可简单说成:两直线平行,同位角相等.
∵a∥b,∴∠1=∠2.
(4)归纳概括:你能否将你得到的结论用数学语言表述?
问题:你用什么方法验证你的猜想? (学生当“小老师”角色)
(1)探索:两直线平行,内错角、同旁内角又有什么关系?
一般地,平行线具有的性质:性质1 两条平行线被第三条直线所截,同位角相等.性质2 两条平行线被第三条直线所截,内错角相等.性质3 两条平行线被第三条直线所截,同旁内角互补.
两直线平行,内错角相等.∵a∥b,∴∠2=∠3.
两直线平行,同旁内角互补.∵a∥b,∴∠2+∠4 =180°.
两直线平行,同位角相等.∵a∥b,∴∠1=∠2.
思考1:你能根据性质1“两直线平行,同位角相等” 推出“两直线平行,内错角相等”吗?
能说明:如图,∵a∥b(已知),∴∠1 =∠2(两直线平行,同位角相等).又∵ ∠3=∠1 (对顶角相等),∴ ∠2 =∠3.
思考2:你能根据性质1“两直线平行,同位角相等” 推出“两直线平行,同旁内角互补”吗?
能说明:如图,∵a∥b(已知),∴∠1=∠2(两直线平行,同位角相等 ).又∵ ∠1+∠4=180°,∴∠2+∠4=180°.
【例1】如图,已知直线a∥b,∠1=50°,求∠2的度数.
【解析】∵a∥b, ∴∠1=∠2(两直线平行,内错角相等) . ∵∠1=50°, ∴∠2=50°.
【例2】 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数.能否求得∠A的度数?
【解析】∵AB∥CD, ∴∠B+∠C=180°(两直线平行,同旁内角互补). ∵∠B=60°,∴∠C=120°. 根据题目的已知条件,无法求出∠A的度数.
1.完成并比较.如图,(1)∵a∥b(已知), ∴∠1___∠2( ).(2)∵ a∥b(已知), ∴∠2___∠3( ).(3)∵a∥b(已知), ∴∠2+∠4=____( ).
= 两直线平行,同位角相等
= 两直线平行,内错角相等
180° 两直线平行,同旁内角互补
2.如图,直线a∥b,∠1=54°,那么∠2 ,∠3 , ∠4 各是多少度?
答案:∠2 = 54°∠3 = 126°∠4 = 54°
1.(成都·中考)如图,已知AB‖ED, ∠ECF=65°,则∠BAC的度数为( )A.115° B.65°C.60° D.25°
2.(中山·中考)如图,已知∠1=70° ,如果CD∥BE,那么∠B的度数为( )A.70° B .100° C.110° D.120°
3.(郴州·中考)下列图形中,由AB‖CD ,能得到∠1=∠2的是( )
4.如图,已知AG‖CF,AB‖CD,∠A=40°,求∠C的度数.
解析: ∵ AG‖CF(已知),
∴ ∠A=∠AEC (两直线平行,内错角相等).
∵ AB‖CD (已知),
∴ ∠C=∠AEC (两直线平行,内错角相等).
∴ ∠C=∠A=40°.
∴ ∠C=∠A(等量代换).
平行线的性质与平行线的判定的联系与区别:
同位角相等.内错角相等.同旁内角互补.
初中数学华师大版七年级上册1 平行线优质ppt课件: 这是一份初中数学华师大版七年级上册1 平行线优质ppt课件,文件包含2平行线的判定课件pptx、3平行线的性质课件pptx、1平行线课件pptx、习题52课件pptx等4份课件配套教学资源,其中PPT共61页, 欢迎下载使用。
人教版七年级下册5.2.1 平行线评课课件ppt: 这是一份人教版七年级下册5.2.1 平行线评课课件ppt,共28页。PPT课件主要包含了定义法,知识回顾,学习目标,课堂导入,新知探究,还有其他解法吗,跟踪训练,内错角,ABDC,同旁内角等内容,欢迎下载使用。
数学七年级下册5.2.1 平行线多媒体教学课件ppt: 这是一份数学七年级下册5.2.1 平行线多媒体教学课件ppt,共27页。PPT课件主要包含了怎样的两条直线平行,知识回顾,学习目标,课堂导入,新知探究,∠2与∠1是同位角,跟踪训练,与∠1是同旁内角,与∠1是内错角,随堂练习等内容,欢迎下载使用。













