2.6有理数的加法课件PPT

这是一份2.6有理数的加法课件PPT，共34页。
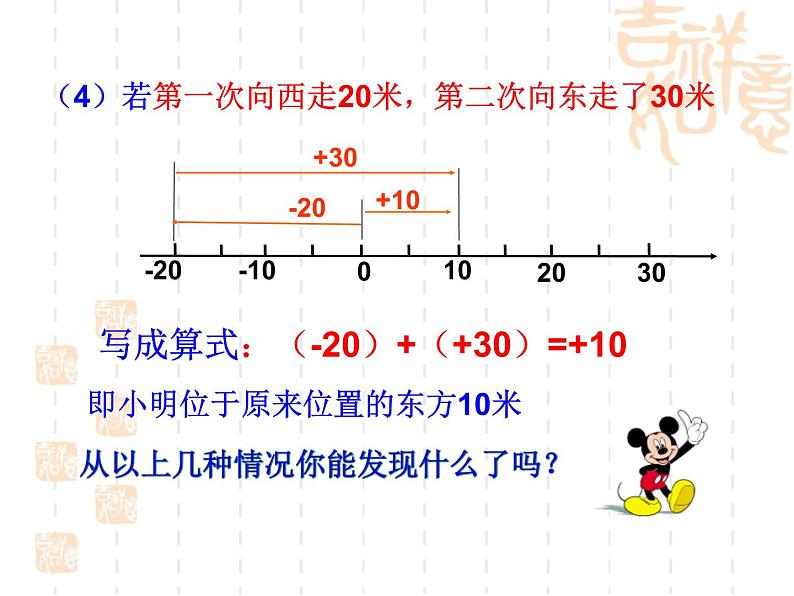
2.6 有理数的加法有理数的加法法则教学目标1．知识与技能:掌握加法法则，体会加法法则的意义。2．过程与方法:通过经历有理数加法运算的发生过程，体验数的运算探索过程，感悟有理数加法运算的技巧及运算规律。通过运算归纳出技巧，感悟绝对值不相等的异号两数相加的技巧，突破本节内容中的难点问题。3．情感、态度与价值观：养成积极探索、不断追求真知的品格。教学重点、难点1.重点：有理数加法法则．2.难点：异号两数相加的法则 一、温故知新、引入课题问题：小明在一条东西向上午跑道上，先走了20米，又走了30米，能否确定他现在的位于原来位置的哪个方向，与原来位置相距多少米？试验：因为这个问题涉及到方向，不妨规定向东为正，向西为负。（1）若两次都是向东走，1030403050-100202050写成算式：（+20）+（+30）=+50即小明位于原来位置的东方50米共向东走了50米（2）若两次都是向西走，10-30-40-30-50-100-20-20-50写成算式：（-20）+（-30）=-50即小明位于原来位置的西方50米则共向西走了50米（3）若第一次向东走20米，第二次向西走了30米1030-30-20-1002020-10写成算式：（+20）+（-30）=-10即小明位于原来位置的西方10米（4）若第一次向西走20米，第二次向东走了30米1030-20+30-100 20-20+10写成算式：（-20）+（+30）=+10即小明位于原来位置的东方10米从以上几种情况你能发现什么了吗？让我们再试几次：（+4）+（+3）= （-5）+（-7）=（+6）+（-8）= （-3）+（+5）=-12+7-2+2同号两数相加，取相同的符号，并把绝对值相加。绝对值不等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。二、  得出法则，揭示内涵再看下面的特殊情况（5）若第一次向西走30米，第二次向东走了30 米。+30-30写成算式：（-30）+（+30）=（ ）0（6）若第一次向西走30米，第二次没走。即小明回到原来的位置写成算式：（-30）+（0）=（ ）-30即小明位于原来位置的西方30米 通过以上探索，你来观察一下，在两个有理数相加的过程中“和的符号”怎样确定？“和的绝对值”怎样确定？一个有理数同0相加，和是多少？议一议有理数的加法法则：（1）同号两数相加，取相同的符号，并把绝对值相加。（2）绝对值不等的异号两数相加，取绝对值较大的加 数的符号，并用较大的绝对值减去较小的绝对值。（3）互为相反数的两数相加得零。（4）一个数与零相加，仍得这个数。注意：一个有理数由符号和绝对值两部分组成，进行加法运算时，应注意确定和的符号和绝对值．阅读下列解题过程，是否有错？若有错，请说出错的原因。 计算 （＋3）＋（－5）解：（＋3）＋（－5）=2正确解法（＋3）＋（－5） =－（5－3） =－2错解分析：本题计算忽略了“先定符号，后计算绝对值”的顺序，因此平时解题时，一定要遵循法则等异号两数相加（取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值）三、强化法则，深入理解解：（1） （+2）+（-11）=-（11-2）=-9（2）（-12）+（+12）=0（3） （ ）+（ ）==-（ + ）（4） （ -3.4）+4.3=+（4.3-3.4）=+0.9四、例题示范，初步运用1、（+4）+（+3）= 2、（+4）+（-3）=3、（+3）+（-10）= 4、（-5）+（+7）=5、（-6）+(+2) = 6、（-4）+（-11）=7、（+30）+（-30）= 8、（-2）+（+2）=9、 0+（-23）= 10、（+16）+0=+7+1-7+2-4-1500-23+16五、分层练习，形成能力计算请你填一填 + 18+8 +26 + 16-9 +7 - 9+5 -14填空1.（ ）+（-3）= -8 2.（ ） +（-3）= 83.（ -3）+（ ）= -1 4.（ - 3）+（ ）= 0 -5 +11 +2 +3 判断1.两数和一定大于每一个加数.（ ）2.两数和一定大于两数绝对值的和.（ ）3.两数和一定小于两数绝对值的和.（ ） 1.两数相加，如果和比每个加数都小，那么这两个数（ ） A、 同为负数 B、异号 C、同为正数 D、零或负数2、如果两数的和为正数，那么一定有（ ）A、一个加数为正，另一个加数为0B、这两个加数都是正数C、一个为正数，另一个为负数，且正数的绝对值较大D、至少有一个加数为正数AD能力拓展3、两数相加，如果和比其中一个加数大，而比另一个加数小，那么这两个数（ ） A、同为负数 B、异号 C、同为正数 D、有一个是04、下面哪个数集中减法总是可以进行的（ ） A、自然数集合 B、有理数集合 C、正数集合 D、负数集合BB这节课的收获是……这节课我们从实例出发，经过比较、归纳，得出了有理数加法的法则．今后我们经常要用类似的思想方法研究其他问题。应用有理数加法法则进行计算时，要同时注意确定“和”的符号，计算“和”的绝对值两件事。1.课本P34页，习题2.6 1，2，2.预习课本P32—P33七、布置作业，引导预习（1）.两个数相加，和一定大于其中一个加数吗？（2）.当三个或三个以上的有理数相加时,你会做吗?3.思考题：——有理数加法的运算律1、同号两数相加，取相同的符号，并把绝对值相加。有理数的加法法则：3、一个数同0相加，仍得这个数。2、绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得0。计算:①(－4)+(－5) ②(－6)+(－6)③－12+0 ④(+9)+(－11) ⑤(－3.78)+(－0.22) ⑥(－6.1)+(+6.1)问题1：在小学中我们学过哪些加法的运算律？问题2：加法的运算律是不是也可以扩充到 有理数范围？探索： 任意选择两个有理数（至少有一个是负数），分别填入下列□和○内，并比较两个运算结果： □ + ○和○ + □ 任意选择三个有理数（至少有一个是负数），分别填入下列□、○和◇内，并比较两个运算结果： ( □ + ○ )+ ◇ 和□ +( ○ + ◇ ).有理数加法中，两个数相加，交换加数的位置和不变。加法交换律：a+b=b+a有理数加法中，三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。加法结合律：(a+b)+c=a+(b+c)例2此题你是抓住数的什么特点使计算简化的？解:(1)原式=26+5+（－18）+（－16） =（26+5）+[（－18）+（－16）]=31+（－34） =－3（1）（+26）+（－18）+5+（－16）；（2）（－1.75）+1.5+（+7.3）+（－2.25）+（－8.5）解:(2)原式= （－1.75） +（－2.25） +1.5+（－8.5） +（+7.3）=[（－1.75）+（－2.25）]+[1.5+(－8.5)]+7.3=（－4）+(－7)+7.3 =(－4)+[(－7)+7.3]（1）（+26）+（－18）+5+（－16）；（2）（－1.75）+1.5+（+7.3）+（－2.25）+（－8.5） =(－4)+0.3 =－3.7　计算(－12)+(+11)+(－8)+(－7)+(+39)+7解：原式＝(－1)+(－8)+(－7)+(+39)+7 =(－9)+(－7)+(+39)+7 =(－16)+(+39)+7 =23+7 =30解：原式＝[(－12)+(－8)]+[(+11)+(+39)]+[(－7)+7] =(－20)+(50)+0 =30谁简便？同分母结合相加常用的三个规律：1、 一般地，总是先把正数或负数分别结合在一起相加。 2、有相反数的可先把相反数相加，能凑成整数的可先凑成整数。 3、有分母相同的，可先把分母相同的数结合相加。 10筐苹果，以每筐30千克为准，超过的千克数记作正数，不足的千克数记作负数，记录如下： 2，－4，2.5，3，－0.5， 1.5，3，－1，0，－2.5 问这10筐苹果总共重多少？例3解：2+(－4)+2.5+3+(－0.5)+1.5+3+(－1)+0+(－2.5)=(2+3+3)+(－4)+[2.5+(－2.5)]+[(－0.5)+(－1)+1.5]=8+(－4)=4故：10筐苹果一共30×10+4＝304千克作业:　 第34页 第3、4题 第35页 第5题