2022年中考高分冲刺压轴题专题特训-特殊平行四边形

这是一份2022年中考高分冲刺压轴题专题特训-特殊平行四边形，文件包含2022中考压轴题高分冲刺专题特训-特殊平行四边形-解析docx、2022中考压轴题高分冲刺专题特训-特殊平行四边形-原卷docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
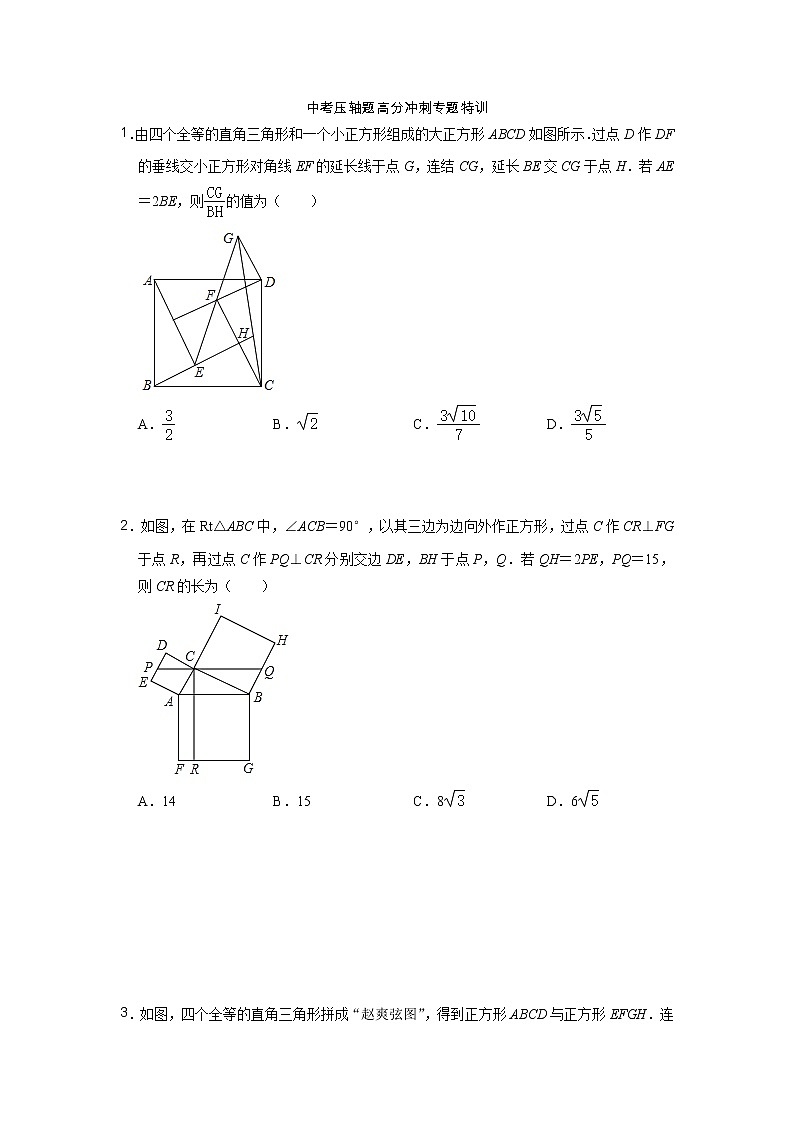
2022中考高分冲刺压轴题专题特训
1．由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．过点D作DF的垂线交小正方形对角线EF的延长线于点G，连结CG，延长BE交CG于点H．若AE＝2BE，则的值为（　　）

A． B． C． D．
【解答】解：如图，过点G作GT⊥CF交CF的延长线于T，设BH交CF于M，AE交DF于N．设BE＝AN＝CM＝DF＝a，则AE＝BM＝CF＝DN＝2a，

∴EN＝EM＝MF＝FN＝a，∵四边形ENFM是正方形，
∴∠EFH＝∠TFG＝45°，∠NFE＝∠DFG＝45°，∵GT⊥TF，DF⊥DG，
∴∠TGF＝∠TFG＝∠DFG＝∠DGF＝45°，∴TG＝FT＝DF＝DG＝a，
∴CT＝3a，CG＝＝a，∵MH∥TG，
∴△CMH∽△CTG，∴CM：CT＝MH：TG＝1：3，∴MH＝a，
∴BH＝2a+a＝a，∴＝＝，故选：C．
2．如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，过点C作CR⊥FG于点R，再过点C作PQ⊥CR分别交边DE，BH于点P，Q．若QH＝2PE，PQ＝15，则CR的长为（　　）

A．14 B．15 C．8 D．6
【解答】解：如图，连接EC，CH．设AB交CR于J．

∵四边形ACDE，四边形BCIH都是正方形，∴∠ACE＝∠BCH＝45°，
∵∠ACB＝90°，∠BCI＝90°，∴∠ACE+∠ACB+∠BCH＝180°，∠ACB+∠BCI＝180°
∴B，C，D共线，A，C，I共线，E、C、H共线，∵DE∥AI∥BH，∴∠CEP＝∠CHQ，
∵∠ECP＝∠QCH，∴△ECP∽△HCQ，∴＝＝＝，∵PQ＝15，
∴PC＝5，CQ＝10，∵EC：CH＝1：2，∴AC：BC＝1：2，设AC＝a，BC＝2a，
∵PQ⊥CR，CR⊥AB，∴CQ∥AB，∵AC∥BQ，CQ∥AB，
∴四边形ABQC是平行四边形，∴AB＝CQ＝10，∵AC2+BC2＝AB2，∴5a2＝100，
∴a＝2（负根已经舍弃），∴AC＝2，BC＝4，∵•AC•BC＝•AB•CJ，
∴CJ＝＝4，∵JR＝AF＝AB＝10，∴CR＝CJ+JR＝14，故选：A．
3．如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接EG，BD相交于点O，BD与HC相交于点P．若GO＝GP，则的值是（　　）

A．1+ B．2+ C．5﹣ D．
【解答】解：∵四边形EFGH为正方形，∴∠EGH＝45°，∠FGH＝90°，
∵OG＝GP，∴∠GOP＝∠OPG＝67.5°，∴∠PBG＝22.5°，又∵∠DBC＝45°，
∴∠GBC＝22.5°，∴∠PBG＝∠GBC，∵∠BGP＝∠BGC＝90°，BG＝BG，
∴△BPG≌△BCG（ASA），∴PG＝CG．设OG＝PG＝CG＝x，
∵O为EG，BD的交点，∴EG＝2x，FG＝x，
∵四个全等的直角三角形拼成“赵爽弦图”，∴BF＝CG＝x，∴BG＝x+x，
∴BC2＝BG2+CG2＝＝，
∴＝．故选：B．
4．【基础巩固】
（1）如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．
【尝试应用】
（2）如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF＝4，BE＝3，求AD的长．
【拓展提高】
（3）如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，∠EDF＝∠BAD，AE＝2，DF＝5，求菱形ABCD的边长．

【解答】解：（1）证明：∵∠ACD＝∠B，∠A＝∠A，∴△ADC∽△ACB，
∴，∴AC2＝AD•AB．
（2）∵四边形ABCD是平行四边形，∴AD＝BC，∠A＝∠C，又∵∠BFE＝∠A，
∴∠BFE＝∠C，又∵∠FBE＝∠CBF，∴△BFE∽△BCF，∴，
∴BF2＝BE•BC，∴BC＝＝，∴AD＝．
（3）如图，分别延长EF，DC相交于点G，

∵四边形ABCD是菱形，∴AB∥DC，∠BAC＝∠BAD，∵AC∥EF，
∴四边形AEGC为平行四边形，∴AC＝EG，CG＝AE，∠EAC＝∠G，
∵∠EDF＝∠BAD，∴∠EDF＝∠BAC，∴∠EDF＝∠G，又∵∠DEF＝∠GED，
∴△EDF∽△EGD，∴，∴DE2＝EF•EG，又∵EG＝AC＝2EF，
∴DE2＝2EF2，∴DE＝EF，又∵，∴DG＝，
∴DC＝DG﹣CG＝5﹣2．
5．如图，在四边形ABCD中，∠A＝∠C＝90°，DE，BF分别平分∠ADC，∠ABC，并交线段AB，CD于点E，F（点E，B不重合）．在线段BF上取点M，N（点M在BN之间），使BM＝2FN．当点P从点D匀速运动到点E时，点Q恰好从点M匀速运动到点N．记QN＝x，PD＝y，已知y＝x+12，当Q为BF中点时，y＝．
（1）判断DE与BF的位置关系，并说明理由．
（2）求DE，BF的长．
（3）若AD＝6．
①当DP＝DF时，通过计算比较BE与BQ的大小关系．
②连接PQ，当PQ所在直线经过四边形ABCD的一个顶点时，求所有满足条件的x的值．

【解答】解：（1）DE与BF的位置关系为：DE∥BF，理由如下：如图1所示：
∵∠A＝∠C＝90°，∴∠ADC+∠ABC＝360°﹣（∠A+∠C）＝180°，
∵DE、BF分别平分∠ADC、∠ABC，∴∠ADE＝∠ADC，∠ABF＝∠ABC，
∴∠ADE+∠ABF＝×180°＝90°，∵∠ADE+∠AED＝90°，∴∠AED＝∠ABF，
∴DE∥BF；
（2）令x＝0，得y＝12，∴DE＝12，令y＝0，得x＝10，∴MN＝10，
把y＝代入y＝﹣x+12，解得：x＝6，即NQ＝6，∴QM＝10﹣6＝4，
∵Q是BF中点，∴FQ＝QB，∵BM＝2FN，∴FN+6＝4+2FN，解得：FN＝2，
∴BM＝4，∴BF＝FN+MN+MB＝16；
（3）①连接EM并延长交BC于点H，如图2所示：∵FM＝2+10＝12＝DE，DE∥BF，
∴四边形DFME是平行四边形，∴DF＝EM，EH∥CD，∴∠MHB＝∠C＝90°，
∵AD＝6，DE＝12，∠A＝90°，∴∠DEA＝30°，∴∠DEA＝∠FBE＝∠FBC＝30°，
∴∠ADE＝60°，∴∠ADE＝∠CDE＝∠FME＝60°，∴∠DFM＝∠DEM＝120°，
∴∠MEB＝180°﹣120°﹣30°＝30°，∴∠MEB＝∠FBE＝30°，
∴∠EHB＝180°﹣30°﹣30°﹣30°＝90°，DF＝EM＝BM＝4，∴MH＝BM＝2，
∴EH＝4+2＝6，由勾股定理得：HB＝＝＝2，
∴BE＝＝＝4，当DP＝DF时，﹣x+12＝4，
解得：x＝，∴BQ＝14﹣x＝14﹣＝，∵＞4，∴BQ＞BE；
②（Ⅰ）当PQ经过点D时，如图3所示：y＝0，则x＝10；
（Ⅱ）当PQ经过点C时，如图4所示：∵BF＝16，∠FCB＝90°，∠CBF＝30°，
∴CF＝BF＝8，∴CD＝8+4＝12，∵FQ∥DP，∴△CFQ∽△CDP，∴＝，
∴＝，解得：x＝；
（Ⅲ）当PQ经过点A时，如图5所示：∵PE∥BQ，∴△APE∽△AQB，
∴＝，由勾股定理得：AE＝＝＝6，
∴AB＝6+4＝10，∴＝，解得：x＝，
由图可知，PQ不可能过点B；综上所述，当x＝10或x＝或x＝时，PQ所在的直线经过四边形ABCD的一个顶点．



6．【性质探究】
如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．
（1）判断△AFG的形状并说明理由．
（2）求证：BF＝2OG．
【迁移应用】
（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．
【拓展延伸】
（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连接EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．

【解答】（1）解：如图1中，△AFG是等腰三角形．

理由：∵AE平分∠BAC，∴∠1＝∠2，∵DF⊥AE，∴∠AHF＝∠AHG＝90°，
∵AH＝AH，∴△AHF≌△AHG（ASA），∴AF＝AG，∴△AFG是等腰三角形．
（2）证明：如图2中，过点O作OL∥AB交DF于L，则∠AFG＝∠OLG．

∵AF＝AG，∴∠AFG＝∠AGF，∵∠AGF＝∠OGL，∴∠OGL＝∠OLG，
∴OG＝OL，∵OL∥AB，∴△DLO∽△DFB，∴＝，∵四边形ABCD是矩形，
∴BD＝2OD，∴BF＝2OL，∴BF＝2OG．
（3）解：如图3中，过点D作DK⊥AC于K，则∠DKA＝∠CDA＝90°，

∵∠DAK＝∠CAD，∴△ADK∽△ACD，∴＝，
∵S1＝•OG•DK，S2＝•BF•AD，又∵BF＝2OG，＝，
∴＝＝，设CD＝2x，AC＝3x，则AD＝x，∴＝＝．
（4）解：设OG＝a，AG＝k．
①如图4中，连接EF，当点F在线段AB上时，点G在OA上．

∵AF＝AG，BF＝2OG，∴AF＝AG＝k，BF＝2a，∴AB＝k+2a，AC＝2（k+a），
∴AD2＝AC2﹣CD2＝[2（k+a）]2﹣（k+2a）2＝3k2+4ka，
∵∠ABE＝∠DAF＝90°，∠BAE＝∠ADF，∴△ABE∽△DAF，
∴＝，即＝，∴＝，∴BE＝，
由题意：10××2a×＝AD•（k+2a），∴AD2＝10ka，即10ka＝3k2+4ka，
∴k＝2a，∴AD＝2a，∴BE＝＝a，AB＝4a，
∴tan∠BAE＝＝．
②如图5中，当点F在AB的延长线上时，点G在线段OC上，连接EF．

∵AF＝AG，BF＝2OG，∴AF＝AG＝k，BF＝2a，∴AB＝k﹣2a，AC＝2（k﹣a），
∴AD2＝AC2﹣CD2＝[2（k﹣a）]2﹣（k﹣2a）2＝3k2﹣4ka，
∵∠ABE＝∠DAF＝90°，∠BAE＝∠ADF，∴△ABE∽△DAF，
∴＝，即＝，∴＝，∴BE＝，
由题意：10××2a×＝AD•（k﹣2a），∴AD2＝10ka，
即10ka＝3k2﹣4ka，∴k＝a，∴AD＝a，
∴BE＝＝a，AB＝a，∴tan∠BAE＝＝，
综上所述，tan∠BAE的值为或．
7．如图，在平面直角坐标系中，正方形ABOC的两直角边分别在坐标轴的正半轴上，分别过OB，OC的中点D，E作AE，AD的平行线，相交于点F，已知OB＝8．
（1）求证：四边形AEFD为菱形．
（2）求四边形AEFD的面积．
（3）若点P在x轴正半轴上（异于点D），点Q在y轴上，平面内是否存在点G，使得以点A，P，Q，G为顶点的四边形与四边形AEFD相似？若存在，求点P的坐标；若不存在，试说明理由．

【解答】（1）证明：如图1中，

∵AE∥DF，AD∥EF，∴四边形AEFD是平行四边形，∵四边形ABOC是正方形，
∴AC＝AB＝OC＝OB，∠ACE＝∠ABD＝90°，∵E，D分别是OC，OB的中点，
∴CE＝BD，∴△CAE≌△ABD（SAS），∴AE＝AD，
∴平行四边形AEFD是菱形．
（2）解：如图1中，连接DE．∵S△ADB＝S△ACE＝×8×4＝16，S△EOD＝×4×4＝8，
∴S△AED＝S正方形ABOC﹣2S△ABD﹣S△EOD＝64﹣2×16﹣8＝24，
∴S菱形AEFD＝2S△AED＝48．
（3）解：如图1中，连接AF，设AF交DE于K，∵OE＝OD＝4，OK⊥DE，
∴KE＝KD，∴OK＝KE＝KD＝2，∵AO＝8，∴AK＝6，∴AK＝3DK，
①当AP为菱形的一边，点Q在x轴的上方，有图2，图3两种情形：
如图2中，设AG交PQ于H，过点H作HN⊥x轴于N，交AC于M，设AM＝t．

∵菱形PAQG∽菱形ADFE，∴PH＝3AH，∵HN∥OQ，QH＝HP，∴ON＝NP，
∴HN是△PQO的中位线，∴ON＝PN＝8﹣t，
∵∠MAH＝∠PHN＝90°﹣∠AHM，∠PNH＝∠AMH＝90°，∴△HMA∽△PNH，
∴＝＝＝，∴HN＝3AM＝3t，∴MH＝MN﹣NH＝8﹣3t，
∵PN＝3MH，∴8﹣t＝3（8﹣3t），∴t＝2，∴OP＝2ON＝2（8﹣t）＝12，
∴P（12，0）．
如图3中，过点H作HI⊥y轴于I，过点P作PN⊥x轴交IH于N，延长BA交IN于M．

同法可证：△AMH∽△HNP，∴＝＝＝，设MH＝t，∴PN＝3MH＝3t，
∴AM＝BM﹣AB＝3t﹣8，∵HI是△OPQ的中位线，∴OP＝2IH，∴HI＝HN，
∴8+t＝9t﹣24，∴t＝4，∴OP＝2HI＝2（8+t）＝24，∴P（24，0）．
②当AP为菱形的边，点Q在x轴的下方时，有图4，图5两种情形：
如图4中，QH＝3PH，过点H作HM⊥OC于M，过D点P作PN⊥MH于N．

∵MH是△QAC的中位线，∴MH＝AC＝4，同法可得：△HPN∽△QHM，
∴＝＝＝，∴PN＝HM＝，∴OM＝PN＝，设HN＝t，则MQ＝3t，
∵MQ＝MC，∴3t＝8﹣，∴t＝，∴OP＝MN＝4+t＝，
∴点P的坐标为（，0）．
如图5中，QH＝3PH，过点H作HM⊥x轴于M交AC于I，过点Q作QN⊥HM于N．

∵IH是△ACQ的中位线，∴CQ＝2HI，NQ＝CI＝4，同法可得：△PMH∽△HNQ，
∴＝＝＝，则MH＝NQ＝，设PM＝t，则HN＝3t，
∵HN＝HI，∴3t＝8+，∴t＝，∴OP＝OM﹣PM＝QN﹣PM＝4﹣t＝，
∴P（，0）．
③如图6中，当AP为菱形的对角线时，有图6一种情形：

过点H作HM⊥y轴于于点M，交AB于I，过点P作PN⊥HM于N．
∵HI∥x轴，AH＝HP，∴AI＝IB＝4，∴PN＝IB＝4，同法可得：△PNH∽△HMQ，
∴＝＝＝，∴MH＝3PN＝12，HI＝MH﹣MI＝4，
∵HI是△ABP的中位线，∴BP＝2IH＝8，∴OP＝OB+BP＝16，∴P（16，0），
综上所述，满足条件的点P的坐标为（12，0）或（24，0）或（，0）或（，0）或（16，0）．
8．定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．
（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．
求证：四边形ABEF是邻余四边形．
（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB是邻余线，E，F在格点上．
（3）如图3，在（1）的条件下，取EF中点M，连接DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．

【解答】解：（1）∵AB＝AC，AD是△ABC的角平分线，
∴AD⊥BC，∴∠ADB＝90°，∴∠DAB+∠DBA＝90°，∠FAB与∠EBA互余，
∴四边形ABEF是邻余四边形；
（2）如图所示（答案不唯一），

四边形AFEB为所求；

（3）∵AB＝AC，AD是△ABC的角平分线，∴BD＝CD，∵DE＝2BE，
∴BD＝CD＝3BE，∴CE＝CD+DE＝5BE，∵∠EDF＝90°，点M是EF的中点，
∴DM＝ME，∴∠MDE＝∠MED，∵AB＝AC，∴∠B＝∠C，∴△DBQ∽△ECN，
∴，∵QB＝3，∴NC＝5，∵AN＝CN，∴AC＝2CN＝10，∴AB＝AC＝10．

9．（2019•绍兴）如图，矩形ABCD中，AB＝a，BC＝b，点M，N分别在边AB，CD上，点E，F分别在边BC，AD上，MN，EF交于点P，记k＝MN：EF．
（1）若a：b的值为1，当MN⊥EF时，求k的值．
（2）若a：b的值为，求k的最大值和最小值．
（3）若k的值为3，当点N是矩形的顶点，∠MPE＝60°，MP＝EF＝3PE时，求a：b的值．

【解答】解：（1）如图1中，

作FH⊥BC于H，MQ⊥CD于Q，设EF交MN于点O．∵四边形ABCD是正方形，
∴FH＝AB，MQ＝BC，∵AB＝CB，∴FH＝MQ，∵EF⊥MN，∴∠EON＝90°，
∵∠ECN＝90°，∴∠MNQ+∠CEO＝180°，∠FEH+∠CEO＝180°
∴∠FEH＝∠MNQ，∵∠EHF＝∠MQN＝90°，∴△FHE≌△MQN（AAS），
∴MN＝EF，∴k＝MN：EF＝1．
（2）∵a：b＝1：2，∴b＝2a，由题意：2a≤MN≤a，a≤EF≤a，
∴当MN的长取最大时，EF取最短，此时k的值最大最大值＝，
当MN的最短时，EF的值取最大，此时k的值最小，最小值为．
（3）连接FN，ME．∵k＝3，MP＝EF＝3PE，∴＝＝3，
∴＝＝2，∵∠FPN＝∠EPM，∴△PNF∽△PME，∴＝＝2，ME∥NF，
设PE＝2m，则PF＝4m，MP＝6m，NP＝12m，
①如图2中，当点N与点D重合时，点M恰好与B重合．作FH⊥BD于H．

∵∠MPE＝∠FPH＝60°，∴PH＝2m，FH＝2m，DH＝10m，
∴＝＝＝．
②如图3中，当点N与C重合，作EH⊥MN于H．则PH＝m，HE＝m，

∴HC＝PH+PC＝13m，∴tan∠HCE＝＝＝，∵ME∥FC，
∴∠MEB＝∠FCB＝∠CFD，∵∠B＝∠D，∴△MEB∽△CFD，
∴＝＝2，∴＝＝＝，
综上所述，a：b的值为或．