北师大版八年级下册第三章 图形的平移与旋转3 中心对称备课ppt课件

这是一份北师大版八年级下册第三章 图形的平移与旋转3 中心对称备课ppt课件，共21页。PPT课件主要包含了学习目标，情境导入，旋转角为180°，探索交流，能够与另一个图形重合，中心对称，对称中心简称中心，你发现了什么，例题解析，中心对称的性质等内容，欢迎下载使用。

1.理解中心对称的概念；(重点)2.能综合运用变换解决有关问题。（难点）
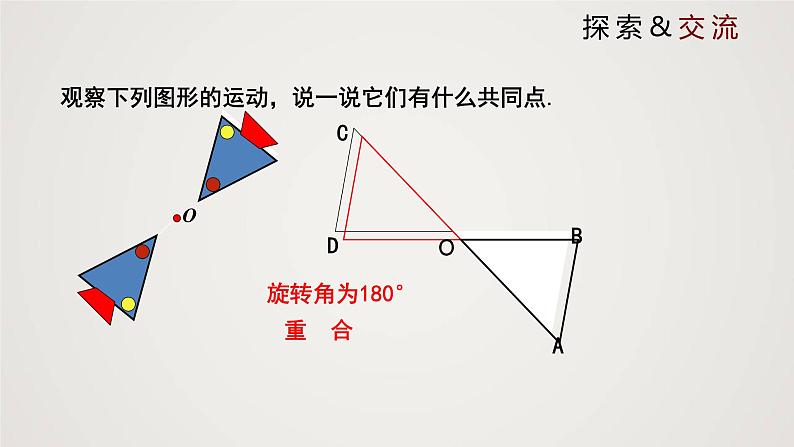
下面图形，它们有何共同特征：
绕某点旋转180°后能与原图形重合.
观察下列图形的运动，说一说它们有什么共同点.
把一个图形 ，如果它 ，那么就说这两个图形关于这个点 或 ，这个点叫做 . 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
1.只有一个对称中心2.旋转角必须是180度3.是两个图形，且旋转后能够重合
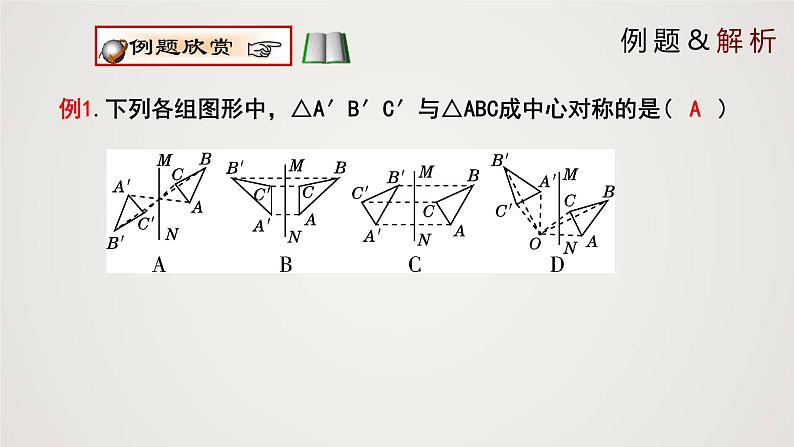
例1.下列各组图形中，△A′B′C′与△ABC成中心对称的是(　　)
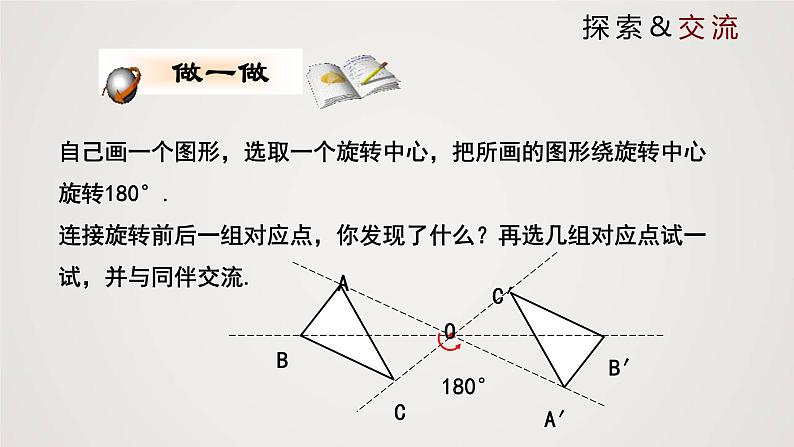
自己画一个图形，选取一个旋转中心，把所画的图形绕旋转中心旋转180°.连接旋转前后一组对应点，你发现了什么？再选几组对应点试一试，并与同伴交流.
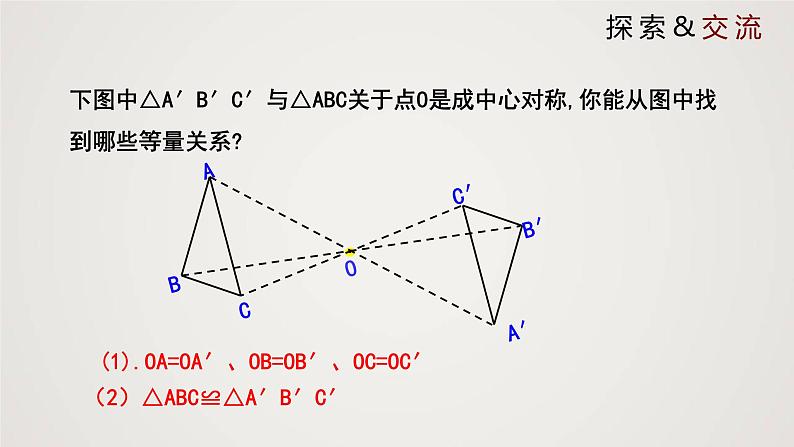
下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系?
(1).OA=OA′、OB=OB′、OC=OC′
（2）△ABC≌△A′B′C′
1.成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分.（即对称点与对称中心三点共线）
2.中心对称的两个图形是全等形.
中心对称与轴对称有什么区别?又有什么联系?
例2.如图，点O是线段AE的中点， 以点O为对称中心，画出与五边形ABCDE成中心对称的图形.
解：如图,连接BO并延长至B′，使 得OB′=OB ;连接CO并延长至C'，使得OC′=OC ;连接DO并延长至D′，使得OD′=OD ; 顺次连接E,B′,C′,D′,A.图形EB′C′D′A就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
观察下图，这些图形有什么共同特征？你还能举出一些类似的图形吗？
把一个图形绕某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心.
注意：中心对称图形是指一个图形.
中心对称与中心对称图形的区别与联系 ：
例3.如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB＝2，BC＝3，则图中阴影部分的面积为_______.
1.如图，在下列图形中，中心对称图形有(　　)A．1个　　B．2个　　C．3个　　D．4个
2.如下所示的4组图形中，左边数字与右边数字成中心对称的有（ ） A.1组 B.2组 C.3组 D.4组
3.下列图形中是中心对称图形而不是轴对称图形的是 ( ）A.平行四边形 B.矩形 C.菱形 D.正方形
中心对称的概念：把一个图形绕着某一点旋转180°,如果旋转后的图形与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心.
中心对称的性质：① 关于中心对称的两个图形是全等形. ② 关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分. ③ 关于中心对称的两个图形，对应线段平行（或者在同一直线上）且相等.