数学七年级下册第12章 证明12.3 互逆命题评课ppt课件

这是一份数学七年级下册第12章 证明12.3 互逆命题评课ppt课件，共19页。PPT课件主要包含了复习回顾，命题1，命题2，互逆命题，命题1和命题2叫做，活动一概念，回顾反思，著名的反例等内容，欢迎下载使用。

1.在数学中，命题一般由 和 构成。
2.如果条件成立，结论成立，那么这样的命题叫做 。如果条件成立，结论不成立，那么这样的命题叫做 。
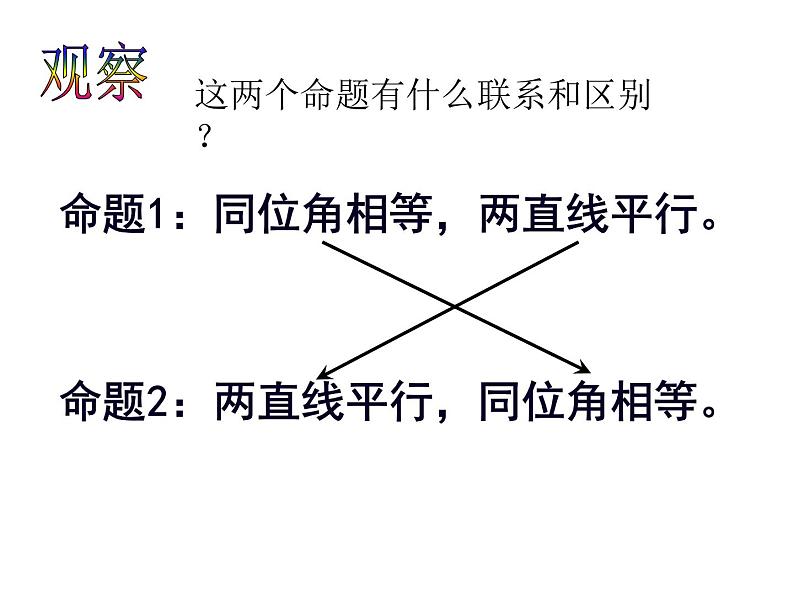
命题1：同位角相等，两直线平行。
命题2：两直线平行，同位角相等。
这两个命题有什么联系和区别？
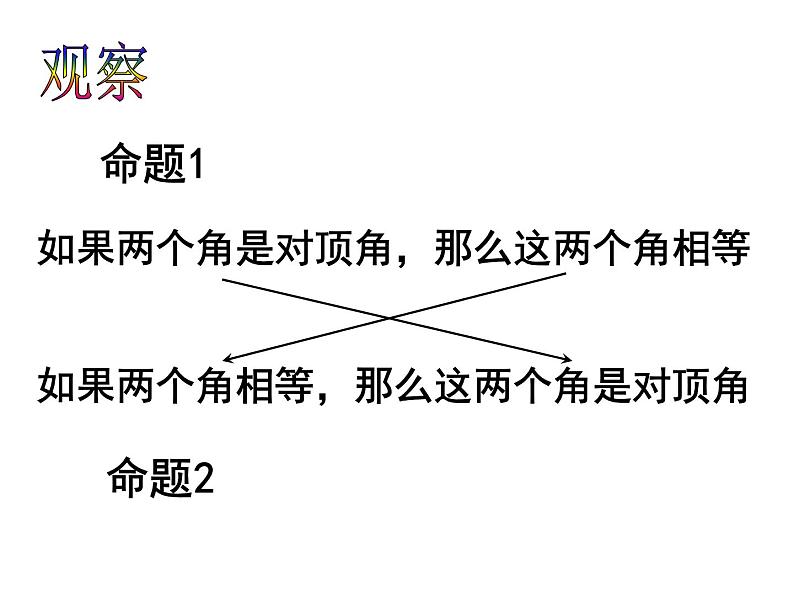
命题1 对顶角相等。
命题2 相等的角是对顶角。
命题1是命题2的逆命题，命题2是命题1的逆命题。
两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题。其中一个命题称为另一个命题的逆命题。
1.下列这些命题中，哪些是互逆命题？
①直角都相等；②内错角相等，两直线平行；③如果a+b>0, 那么a>0,b>0；④相等的角都是直角；⑤如果a>0,b>0, 那么ab>0；⑥两直线平行，内错角相等。
③如果a+b>0, 那么a>0,b>0；⑤如果a>0,b>0, 那么ab>0。
如果a>0,b>0, 那么a+b>0 ；
如果ab>0, 那么a>0,b>0 。
把一个命题的条件和结论互换就得到它的逆命题，所以每个命题都有逆命题。
1．下列各组命题是否是互逆命题：
12.3　互逆命题（1）
（4）“同位角相等，两直线平行”与“同位角不相等，两直线不平行” ．
（3）“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”；
（2）“对顶角相等”与“如果两个角相等，那么这两个角是对顶角”；
（1）“等于同一个角的两个角相等”与“如果两个角都等于同一个角，那么这两个角相等”；
:说出下列命题的逆命题，并与同学交流：
①轴对称图形是等腰三角形；
等腰三角形是轴对称图形；
如果两个角相等，那么这两个角是同一个角的补角；
③直角三角形的两个锐角互余；
有两个角互余的三角形是直角三角形；
④正方形的4个角都是直角；
如果一个四边形的4个角都是直角，那么这个四边形是正方形。
说出下列命题的逆命题，并判断每对互逆命题的真假．（1）如果a＝b，那么a2＝b2；（2）如果两个角是对顶角，那么它们的平分线在同一条直线上；（3）末位数字是5的数，能被5整除；（4）锐角与钝角互为补角.
逆命题：如果a2＝b2，那么a＝b .
逆命题：如果两个角的平分在同一条直线上，那么这两个角是对顶角.
逆命题：能被5整除的数，末位数字是5.
逆命题：如果两个角互为补角，那么这两个角一个是锐角一个是钝角．
一对互逆命题的真假性不一定相同！
举反例说明下列命题是假命题：（1）如果|a|＝|b| ，那么a＝b；（2）任何数的平方大于0；（3）两个锐角的和是钝角；（4）如果一点到线段两端的距离相等，那么这点是这条线段的中点．
　　公元１６４０年，法国著名数学家费尔马发现：　　　２２０＋１＝３，　　　２２１＋１＝５，　　 ２２２＋１＝１７，　　 ２２３＋１＝２５７，　　　２２４＋１＝６５５３７．而3、5、17、257、65 537都是质数，于是费尔马猜想：