人教版七年级下册6.3 实数教案设计

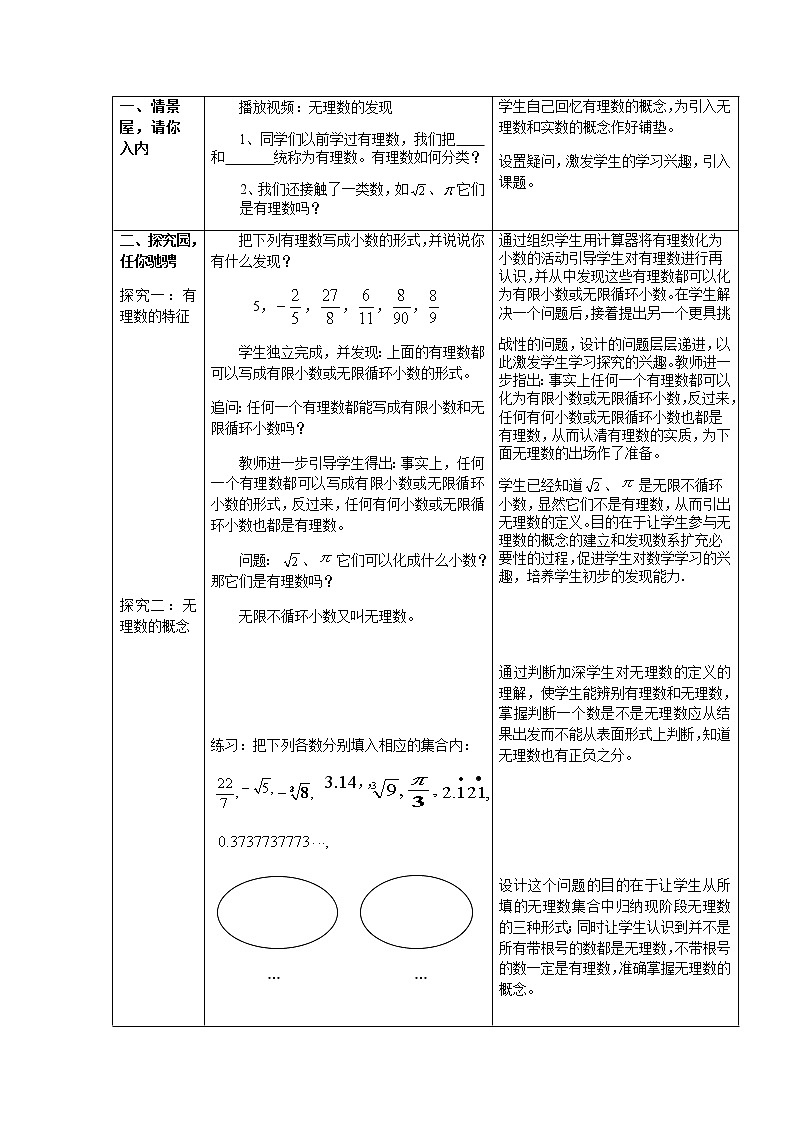
这是一份人教版七年级下册6.3 实数教案设计，共5页。教案主要包含了情景屋，请你入内，探究园，任你驰骋，快乐厅，练中生趣，沉思阁，提练观点，作业坊，各有收获等内容，欢迎下载使用。
  6.3实数教学目标知识技能1、了解无理数和实数的概念；2、会对实数按照一定的标准分类；3、知道实数与数轴上的点一一对应。数学思考1、通过无理数的引入，培养学生从特殊到一般、具体到抽象的逻辑思维能力；2、通过类比有理数的分类方法对实数进行分类，发展学生的分类意识，体会其中渗透的类比思想；3、通过在数轴上表示无理数，体会数形结合的思想。问题解决1、通过无理数的引入，使学生对数的认识由有理数扩充到实数；2、在按不同标准给实数分类的过程中，培养学生的分类能力；3、掌握实数的概念，增强学生应用数学的意识，提高学生应用数学的能力；4、通过探究在数轴上表示无理数，增强学生的探究能力。    情感态度1、经历无理数的发现过程，激发学生的求知欲，使学生感受数学活动充满了探索性与创造性，体验发现的快乐，获取成功的体验；2、通过丰富的数学活动，增强学生克服困难的信心及合作交流的能力。教学重难点重点：1、无理数的概念2、实数的概念和分类难点：1、无理数的概念2、理解实数与数轴上的点一一对应教学过程教学环节师生活动设计意图一、情景屋，请你入内播放视频：无理数的发现1、同学们以前学过有理数，我们把       和       统称为有理数。有理数如何分类？2、我们还接触了一类数，如、它们是有理数吗？学生自己回忆有理数的概念，为引入无理数和实数的概念作好铺垫。设置疑问，激发学生的学习兴趣，引入课题。二、探究园，任你驰骋探究一：有理数的特征        探究二：无理数的概念                    探究三：实数的概念及分类               把下列有理数写成小数的形式，并说说你有什么发现？5，，，，，学生独立完成，并发现：上面的有理数都可以写成有限小数或无限循环小数的形式。追问：任何一个有理数都能写成有限小数和无限循环小数吗？ 教师进一步引导学生得出：事实上，任何一个有理数都可以写成有限小数或无限循环小数的形式，反过来，任何有何小数或无限循环小数也都是有理数。问题： 、它们可以化成什么小数？那它们是有理数吗？无限不循环小数又叫无理数。   练习：把下列各数分别填入相应的集合内：      …                   … 有理数集合           无理数集合根据你所看到的或想到的,你觉得无理数都有哪些形式？·目前为止常见的无理数有三种类型:1.  含型  2．开不尽方的根号型3．构造型（有一定的规律，但不循环的无限小数）思考：带根号的数一定是无理数吗？不带根号的数一定是有理数吗？ 1．有理数和无理数统称为实数2．你还记得有理数的分类吗？你能类比有理数的分类方法对实数进行分类吗？（让学生先回顾有理的分类方法，然后通过类比对实数进行分类）（1）按定义分 0     （2）按大小分       通过组织学生用计算器将有理数化为小数的活动引导学生对有理数进行再认识，并从中发现这些有理数都可以化为有限小数或无限循环小数。在学生解决一个问题后，接着提出另一个更具挑战性的问题，设计的问题层层递进，以此激发学生学习探究的兴趣。教师进一步指出：事实上任何一个有理数都可以化为有限小数或无限循环小数，反过来，任何有何小数或无限循环小数也都是有理数，从而认清有理数的实质，为下面无理数的出场作了准备。学生已经知道、是无限不循环小数，显然它们不是有理数，从而引出无理数的定义。目的在于让学生参与无理数的概念的建立和发现数系扩充必要性的过程，促进学生对数学学习的兴趣，培养学生初步的发现能力. 通过判断加深学生对无理数的定义的理解，使学生能辨别有理数和无理数，掌握判断一个数是不是无理数应从结果出发而不能从表面形式上判断，知道无理数也有正负之分。   设计这个问题的目的在于让学生从所填的无理数集合中归纳现阶段无理数的三种形式；同时让学生认识到并不是所有带根号的数都是无理数，不带根号的数一定是有理数，准确掌握无理数的概念。上面各个环节为引入实数的概念及对实数进行分类作好准备。  教师引学生类比有理数的分类对实数进行分类，体会类比的数学思想，并使学生认识到分类标准不同分类结果也不同，但分类的基本原则都是不重不漏。           三、快乐厅，练中生趣 1、下列说法正确的是（   ） A.  　是无理数    B.   　是分数 C.   　是无理数   D. 　   是无理数 2、在实数                                     中无理数的个数是（  ）A.1个    B.2个   C.3个   D.4个3、下列说法中正确的是         （填写序号）①无限小数都是无理数②无理数都是无限小数 ③实数可以分为正实数和负实数两类 ④无理数包括正无理数、零、负无理数⑤带根号的数都是无理数⑥有理数都是有限小数   通过练习，再次巩固无理数、实数的概念及分类以及实数与数轴的一一对应关系。   四、沉思阁，提练观点         五、作业坊，各有收获这节课你学到了哪些知识？还有什么困惑？渗透了哪些数学思想？         必做：      课本习题6.3第1、2、题选做：      查阅资料，了解无限不循环小数化分数的方法        通过共同小结使学生归纳、梳理总结本节的知识、技能、方法，将本课所学的知识与以前所学的知识进行紧密联结，再一次突出本节课的学习重点，改善学生的学习方式。有利于培养学生数学思想、数学方法、数学能力和对数学的积极情感．同时为以后的学习作知识储备. 分层布置作业，尊重学生个体差异，使不同学生得到不同的发展