小学数学西师大版六年级下册数与代数复习课件ppt

这是一份小学数学西师大版六年级下册数与代数复习课件ppt，共50页。PPT课件主要包含了第一课时，二汇报整理，自然数0和整数，十进制计数法，整数的读法和写法，四舍五入法，整数大小的比较，正负数，正负数的比较，小数的读法和写法等内容，欢迎下载使用。

看课本72页的内容，思考下列问题：（1）我们学过的数有哪几种？（2）这些数之间有什么关系？（3）如果要把这些数分类，可以怎样分？
一、引入情境，回顾旧知
预设：①学生按照整数、小数、分数、百分数分类。②自然数和整数分类。
小学阶段我们研究的自然数包括正整数和零，除此之外，我们还研究了负整数。接下来，我们就对这些数的知识进行复习，整理。
问：想一想，整数和自然数的范围哪个更大？
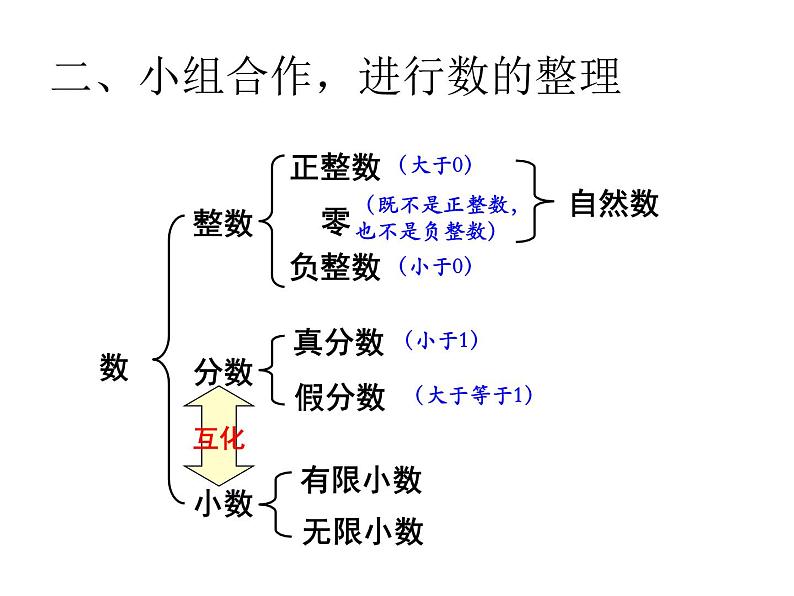
二、小组合作，进行数的整理
（一）小组合作，整理概念
整理提示：1. 根据数的特点找到数之间的联系，并用树形图的形式进行整理。2. 先小组讨论它们之间的联系，然后分工合作，汇报时要说清整理的理由。3. 如果不能够面面俱到，可以选取一部分数进行整理。
1. 汇报，说说自己分类的理由。
2. 边回顾整理过程，边完善知识整理的步骤。
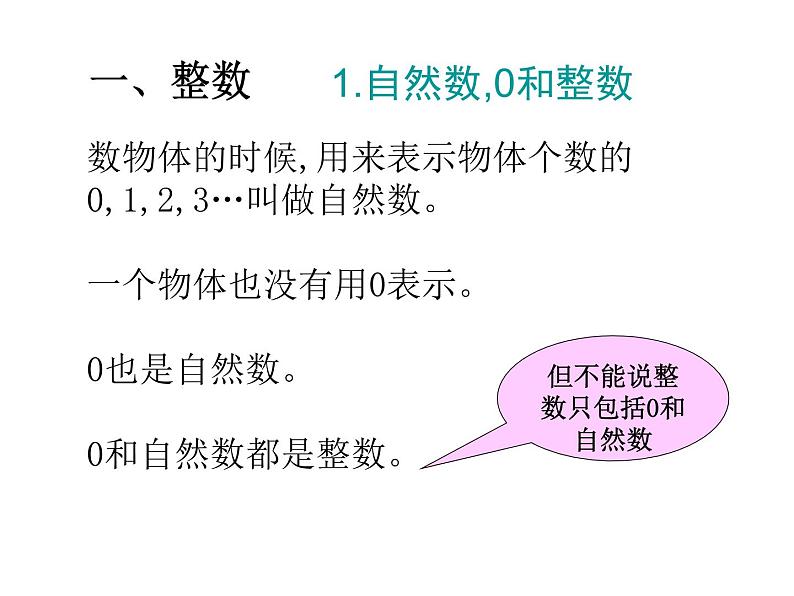
（既不是正整数，也不是负整数）
数物体的时候,用来表示物体个数的0,1,2,3…叫做自然数。一个物体也没有用0表示。0也是自然数。0和自然数都是整数。
但不能说整数只包括0和自然数
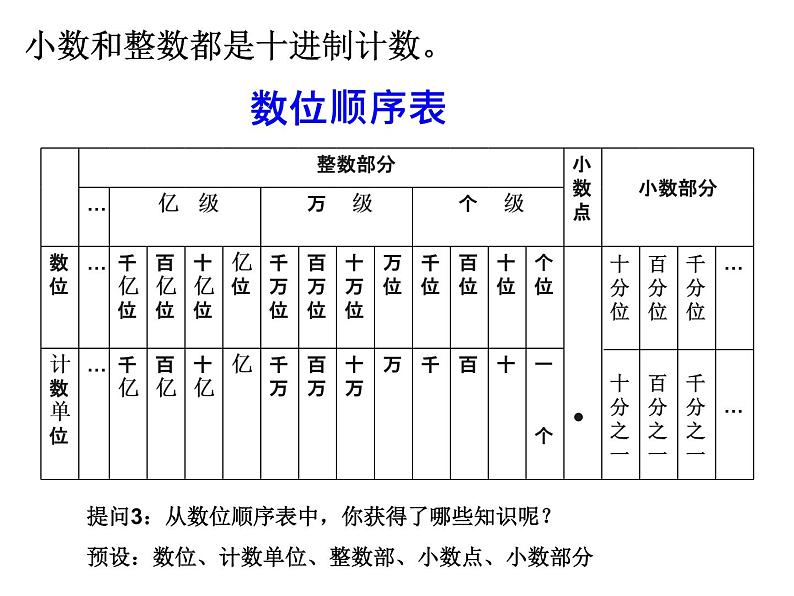
一(个)、十、百、千、万……都叫做计数单位。其中“一”是计数的基本单位。 10个一是十,10个十是百……10个一百亿是一千亿……每相邻两个计数单位之间的进率都是十。这种计数方法叫做十进制计数法。
提问3：从数位顺序表中，你获得了哪些知识呢？
预设：数位、计数单位、整数部、小数点、小数部分
小数和整数都是十进制计数。
请问30.4和3.6这两个数中的“3”含义相同吗？
问：同样是“3”，为什么含义不同？
问：谁能分别说说它们的含义？
小结：看来同样的数字，所在数位不同，表示的含义也就不同。
所在数位不同，计数单位也就不同。
问：你能举例说说1万和1亿到底有多大吗？
读数时,从高位起,一级一级地往下读,属于亿级和万级的要读出级名。 读数时,每级末尾的“0”都不读,其他数位有一个0或连续几个0都只读一个0。8000406000读作:
写数时,从高位起,一级一级地往下写,哪一位上一个单位也没有,就在哪个数位上写0。
六亿八千四百五十二万八千五百六十三
684528563读作:
求一个数的近似数,要看尾数的最高位上的数是几,如果比5小,就把尾数都舍去;如果尾数最高位上的数是5或大于5,就把尾数舍去后,要向它的前一位进1。
比较两个多位数的大小,首先看它们位数的多少,位数较多的数较大; 如果两个数的位数相同,那么首先看最高位,最高位上的数较大的,这个数就大; 如果最高位相同,则左边第二位上的数较大的,这个数就大……
零下11摄氏度比零度还要低11度，可以用－11℃表示。
5摄氏度是在零度以上，是零上温度，可以用5℃表示。
像5、7.6、20、120……都是正数；可以在正数前面添上“+”号，如＋5，＋7.6，＋20，＋120。
像－11、－2、-3.4、-20……都是负数，“-”在这里不是减号，是负号。
请判断：5 > -1 -3 > -2-15 < -100 < -2
正数：数值越大，就表示它越大。负数：数值越大，就表示它越小。
正数、0、负数、小数、分数都可以用数轴清楚地表示出来
提问2：观察数轴，你发现了什么？
预设：数轴上的正、负数是以0为对称点对应排列的。没有最大的整数也没有最小的整数，也就是说整数个数是无限的。正数和负数中都存在着整数、分数、小数。
提问1：你能在数轴上表示出 、2.5、－ 、－2.5这几个数吗？
把整数“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示。 小数点右边第一位是十分位,计数单位是十分之一;第二位是百分位,计数单位是百分之一…… 小数部分的最大计数单位是十分之一,没有最小的计数单位。 小数部分有几个数位,就叫做几位小数。
读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字。 写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
如 45.469 读作:
小数的末尾添上0或者去掉0,小数的大小不变。
运用小数的性质,可以在小数末尾添上0。3.5=3.50
也可以把小数化简。3.500=3.5
4.小数点数位移动引起小数大小的变化
小数点向右(左)移动一位、两位、三位……原来的数就扩大(缩小)10倍、100倍、1000倍…… 如果要把一个数扩大或缩小10倍、100倍……只需要移动小数点,数位不够时用0补足。
一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫做循环小数。如 0.5555…… 7.23838…… 依次不断重复出现的数字叫做循环节。 循环小数的简便记法0.5555…… 记作……记作:7.238
循环节从小数部分第一位开始的叫纯循环小数。如 0.5 循环节不是从小数部分第一位开始的叫混循环小数。如7.238
(1) 按小数位数是有限还是无限分
(2) 按小数的整数部分是否为0分
一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。有时还可以根据需要,省略这个数某一位后面的尾数,写成近似数。把76450000改写成用“万”作单位的数是( )把235800改写成用“万”作单位的数是( )235800省略万位后面的尾数约为( )把34562800000改写成用“亿”作单位的数后,保留两位小数是( )
4.62975保留两位小数是:( )4.62975保留三位小数是:( )
预设：把单位“1”平均分成若干份，表示其中一份的数 叫做分数单位。像一（个）、十、百、千、万、 十万……以及十分之一，百分之一……等，是整数、小数的 计数单位。每相邻两个计数单位之间的进率是 “十”。
问：整数与小数有哪些联系与区别？
预设：整数和小数都是按十进制计数法写出的数，其中个、十、 百……以及十分之一、百分之一……都是计数单位。 各个计数单位所占的位置，叫做数位。数位是按一定顺序排列的。 整数的最小计数单位是1，而小数没有最小的计数单位。
提问10：分数单位与整数、小数的计数单位有什么不同？
1.分数的意义和分数单位
一个物体,一个计量单位或是许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”
把单位“1”平均分成若干份,表示其中的一份的数。
把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数。
预设： 把单位“1”平均分成若干份，表示其中一份的数叫做分数单位。 像一（个）、十、百、千、万、十万……以及十分之一，百分之一……等，是整数、小数的计数单位。每相邻两个计数单位之间的进率是 “十”。
问：分数单位与整数、小数的计数单位有什么不同？
把单位“1”平均分成9份,取其中的5份。
把5米平均分成9份,每份是( ),每份是( )米。
★分母相同的两个分数,分子大的分数比较大。
★分子相同的两个分数,分母小的分数比较大。
★通分:先求出原来几个分母的最小公倍数,然后把各个 分数分别化成用这个最小公倍数作分母的分数。
真分数----假分数----
分子比分母大或者分子和分母相等的分数。
分数的分子和分母同时乘以或者除以相同的数(零除外),分数的大小不变。
一个分数的分母不变,分子乘以3,则这个分数( )如果分子不变,分母除以5,则这个分数( )
*计算的结果,能约分的要约成最简分数;
*判断一个最简分数能不能化成有限小数:
分母中除了2和5以外,不含有其他的质因数,就能化成有限小数。
约分------把一个分数化成和它相等,但分子和分母 都比较小的分数。
约分的方法:1.用分子分母的公约数(1除外)逐次去除分子和 分母,直到得到最简分数为止。2.用分子和分母的最大公约数去除分子和分母。
表示一个数是另一个数的百分之几的数叫百分数。百分数又叫百分率或百分比。
问：百分数是分数中的一种特殊形式。二者的联系与区别是什么？
①联系：都能表示一个数与另一个数之间的比率， 百分数所表示的含义是一个数与另一个数的百分之几， 是分数的一种特殊表示形式。分数和百分数可以互相转化。②区别： 百分数和分数的写法不同； 分数既可以表示率，也可以表示量，但百分数只可以表示率； 分数可以约成最简分数，可是百分数不能进行约分； 分数的分子只能是整数，而百分数的分子既可以是整数，也可以是小数。
10.分数、小数、百分数的互化
0.25=( )
小数点向右移动两位,添上%
0.35%=( )
去掉%,小数点向左移动两位
先化成小数,再化成百分数
≈0.167=16.7%
1. 整除与除尽2. 因数和倍数3. 能被2.3.5整除的数的特征4. 偶数和奇数5. 质数和合数6. 质因数和分解质因数7. 最大公约数和最小公倍数
整数a除以整数b(b≠0),除得的商是整数而没有余数,我们就说数a能被数b整除,或数b能整除a。
数a除以数b(b≠0),除得的商是整数或是有限小数,这就叫做除尽。
整除是除尽的一种特殊情况,整除也可以说是除尽,但除尽不一定是整除。
如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数。
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
因数和倍数是相互依存的
结合算式说一说谁是谁的因数？谁是谁的倍数？
出示算式： ①18÷2＝9 ②2.4÷6＝0.4 ③30÷8＝ ④30÷5＝6 ⑤8÷16＝0.5 ⑥12÷0.3＝40
3. 2.3.5的倍数的特征
个位上是0,2,4,6,8,
各个数位上的数字之和是3的倍数
既是2的倍数,又是5的倍数的数的特征:
既是2和5的倍数，同时又是3的倍数的数的特征:
个位是0,而且各个数位上的数字之和是3的倍数.
注意:有一些数能被7,9,11,13整除,但是不容易看出来, 这是大家在约分中容易忽略的.
练习：一个数既是21的倍数，又是21的因数，这个数是（ ）。
一个自然数,不是奇数就是偶数
是2的倍数的数叫做偶数
不是2的倍数的数叫做奇数
偶数±偶数=( ) 奇数±奇数=( ) 偶数±奇数=( )
偶数×偶数=( ) 奇数×奇数=( ) 偶数×奇数=( )
正方形的边长为整厘米数，它的周长是奇数还是偶数？面积呢？
只有1和它本身两个因数
除了1和它本身还有别的因数
1: 既不是质数，也不是合数
6. 质因数和分解质因数
每一个合数都可以写成几个质数相乘的形式,这几个质数叫做这个合数的质因数。
把一个合数用几个质因数相乘的形式表示出来.叫做分解质因数.
分解质因数的方法:短除法
把30分解质因数正确的做法是( )A.30=1×2 ×3 ×5B.2 ×3 ×5=30C.30=2×3×5
7. 最大公因数和最小公倍数
几个数公有的因数,叫做这几个数的公因数;其中最大的一个叫做这几个数的最大公因数.
例:( )是8和12的公因数,( )是8和12的最大公因数.
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
例:( …)都是4和6的公倍数,( )是4和6的最小公倍数.
公因数只有1的两个数叫做互质数.
⑴、两个不同的质数一定互质.⑵、相邻的两个数互质.⑶、1和任何数都互质.⑷、2和任何奇数都互质
求最大公因数和最小公倍数
4和28 最大公因数是( ); 最小公倍数是( )
⑴.如果两个数是倍数关系,那么较小数就是这两个数的最大公因数;较大数就是这两个数的最小公倍数.
4和15 最大公因数是( ); 最小公倍数是( )
⑵.如果两个数互质,它们的最大公因数就是1;最小公倍数就是它们的积。
求24和36的最大公因数和最小公倍数
24和36的最大公因数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
求出下面各组数的最大公因数和最小公倍数。