中考总复习矩形、菱形、正方形 精品整理 含各类中考真题课件PPT

这是一份中考总复习矩形、菱形、正方形 精品整理 含各类中考真题课件PPT，共42页。PPT课件主要包含了中考命题规律分析，考点知识归纳，平行四边形，正方形，温馨提示，例题精析，考点训练，①③④，课堂训练，中考典型例题解析等内容，欢迎下载使用。
特殊平行四边形是历年中考必考内容之一，题型以选择题、填空题为主，更多以证明题、求值计算题及探索性问题、几何动态问题呈现，试题强调基础，突出能力，源于教材，变中求新，考察学生发散思维能力。
1．定义：有一个角是________的平行四边形是矩形．2．性质：(1)矩形的四个角都是________；(2)矩形的对角线互相平分且________；(3)矩形既是轴对称图形，又是________对称图形， 它有两个对称轴，它的对称中心是对角线的交点．3．判定：(1)有一个角是________的平行四边形是矩形；(2)有_____个角是直角的四边形是矩形；(3)对角线________的平行四边形是矩形．
考点一 矩形的定义、性质和判定
考点二 菱形的定义、性质和判定1．定义：有一组邻边________的平行四边形是菱形． 2．性质：(1)菱形的四条边都________，对角线互相________，并且每条对角线________一组对角；(2)菱形既是轴对称图形又是中心对称图形．3．判定：(1)有一组邻边________的平行四边形是菱形；(2) 四条边都________的四边形是菱形；(3)对角线互相________的平行四边形是菱形．
1．定义： 有一个角是________的菱形是正方形或有一组邻边相等的________是正方形．2．性质： (1)正方形四个角都是________，四条边都________； (2)正方形两条对角线________，并且互相________， 每条对角线平分一组对角． (3)正方形既是轴对称图形又是中心对称图形．3．判定： (1)有一个角是________的菱形是正方形； (2)有一组邻边________的矩形是正方形.
考点三 正方形的定义、性质和判定：
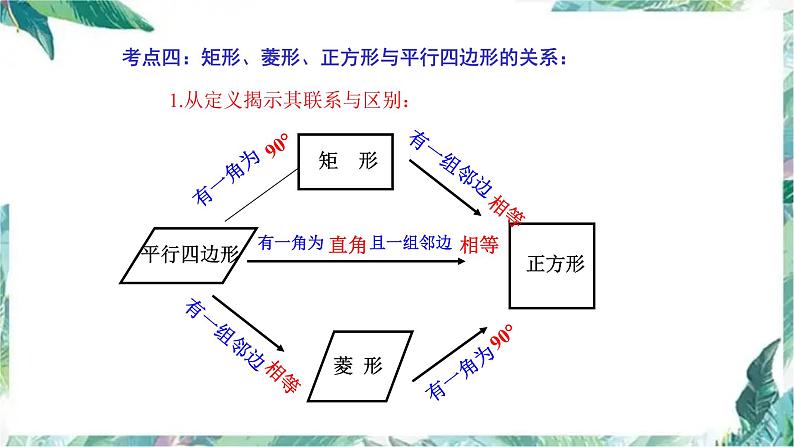
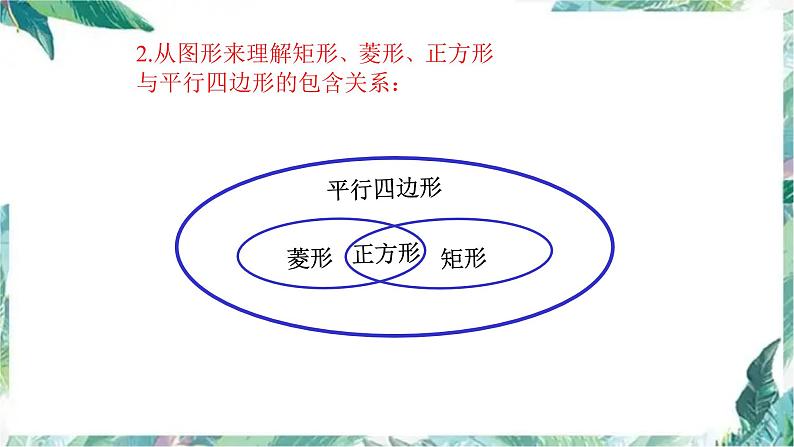
考点四：矩形、菱形、正方形与平行四边形的关系：
有一角为 且一组邻边
1.从定义揭示其联系与区别：
2.从图形来理解矩形、菱形、正方形与平行四边形的包含关系：
1.矩形、菱形、正方形具有平行四边形的所有性质；2.平行四边形及特殊平行四边形的有关知识点比较多，要做到准确而不混淆就要从“边、角、对角线、对称性”四个方面来研究它们的性质和判定，多用数形结合法，熟练掌握它们的区别和联系，把握它们的特征是关键。
典例1　(矩形的判定与性质)如图，四边形ABCD中，对角线AC，BD相交于点O，AO＝OC，BO＝OD，且∠AOB＝2∠OAD.   
(1)求证：四边形ABCD是矩形；∵AO＝OC，BO＝OD，∴四边形ABCD是平行四边形，∵∠AOB＝∠DAO＋∠ADO＝2∠OAD，∴∠DAO＝∠ADO，∴AO＝DO，∴AC＝BD，∴四边形ABCD是矩形．
(2)若∠AOB︰∠ODC＝4︰3，求∠ADO的度数．∠ADO＝36°.
典例2　(菱形的性质与判定)如图，将△ABC沿着AC边翻折，得到△ADC，且AB∥CD.   
(1)判断四边形ABCD的形状，并说明理由；四边形ABCD是菱形．
(2)若AC＝16，BC＝10，求四边形ABCD的面积．
典例3　如图，点E为正方形ABCD外一点，∠AEB＝90°，将Rt△ABE绕A点逆时针方向旋转90°得到△ADF，DF的延长线交BE于H点．
(1)试判定四边形AFHE的形状，并说明理由；四边形AFHE是正方形，理由如下：∵Rt△ABE绕A点逆时针方向旋转90°得到△ADF，∴Rt△ABE≌Rt△ADF，∴∠AEB＝∠AFD＝90°，∴∠AFH＝90°，∵Rt△ABE≌Rt△ADF，
∴∠DAF＝∠BAE，又∵∠DAF＋∠FAB＝90°，∴∠BAE＋∠FAB＝90°，∴∠FAE＝90°，在四边形AFHE中，∠FAE＝90°，∠AEB＝90°，∠AFH＝90°，∴四边形AFHE是矩形，又∵AE＝AF，∴矩形AFHE是正方形；
(2)已知BH＝7，BC＝13，求DH的长．DH＝17.
5．如图，AD∥FE，点B，C在AD上，∠1＝∠2，BF＝BC.(1)求证：四边形BCEF是菱形；
(2)若AB＝BC＝CD，求证：△ACF≌△BDE.
　　　　　6．如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC＝12，点P在正方形的边上，则满足PE＋PF＝9的点P的个数是(　 )   A．0B．4 C．6D．8
例1. (1)下列命题中是真命题的是(　　)A ．对角线相等的四边形是矩形B ．对角线互相垂直的四边形是菱形C ．对角线互相垂直且相等的四边形是正方形D ．对角线互相垂直平分且相等的四边形是正方形
【点拨】本组题综合考查矩形、菱形、正方形的性质和判定
(3)如图，在菱形ABCD中，AB＝15，∠ADC＝120°，则B、D两点之间的距离为(　　)A．15　　　　　 B.C．7.5　　　　 D．15
例2．如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD.(1)试判断四边形OCED的形状，并说明理由；(2)若AB＝6，BC＝8，求四边形OCED的面积．
解：(1)四边形OCED是菱形．理由：∵DE∥AC，CE∥BD，∴四边形OCED是平行四边形．又∵在矩形ABCD中，OC＝OD.∴四边形OCED是菱形．
【点拨】本题综合考查菱形的判定和面积的计算
【解答】(1)在等边△ABC中，∵点D是BC边的中点，∴∠DAC＝30°.又∵△ADE是等边三角形，∴∠DAE＝60°.∴∠CAE＝∠DAE－∠DAC＝60°－30°＝30°.
例3.如图，在等边三角形ABC中，点D是BC边的中点，以AD为边作等边三角形ADE.(1)求∠CAE的度数；(2)取AB边的中点F，连结CF、CE，试证明四边形AFCE是矩形
【点拨】本题综合考查等边三角形的性质和矩形的判定
(2)由(1)知，∠EAF＝90°.由F为AB的中点∠CFA＝90°，∴CF∥EA.在等边三角形ABC中，CF＝AD.在等边三角形ADE中，AD＝EA，∴CF＝EA.∴四边形AFCE为平行四边形．又∵∠CFA＝90°，∴四边形AFCE为矩形．
1.如图，将边长为8 cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，则线段CN的长度为(　　)A．3 cm B．4 cm C．5 cm D．6 cm
【点拨】本题综合考查正方形、图形折叠及直角三角形的性质
2．如图，在边长为2 cm的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连结PB、PQ，则△PBQ周长的最小值为________cm(结果不取近似值)．
【点拨】本题综合考查轴对称、正方形的对称性及直角三角形的性质
【点拨】本题综合考查菱形的判定和全等三角形的判定
3.如图，AD∥FE，点B、C在AD上，∠1＝∠2，BF＝BC.(1)求证：四边形BCEF是菱形；(2)若AB＝BC＝CD，求证：△ACF≌△BDE
（1)证明：∵AD∥FE，∴∠FEB＝∠2.∵∠1＝∠2，∴∠FEB＝∠1，∴BF＝EF.∵BF＝BC，∴BC＝EF，∴四边形BCEF是平行四边形．又∵BF＝BC，∴平行四边形BCEF是菱形．
(2)证明：∵EF＝BC，AB＝BC＝CD，AD∥FE.∴四边形ABEF、四边形CDEF均为平行四边形．∴AF＝BE，FC＝ED，又∵AC＝2BC＝BD，∴△ACF≌△BDE(SSS)．
4.如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F.(1)求证：EO＝FO；(2)当点O运动到何处时，四边形AECF是矩形？并证明你的结论．(3)在(2)的条件下，当△ABC满足什么条件时，四边形AECF是正方形？
证明：(1)∵MN∥BC，∴∠FEC＝∠BCE.∵CE平分∠ACB，∴∠ECB＝∠ACE，∴∠FEC＝∠ACE，∴OE＝OC.同理可证OF＝OC，∴OE＝FO.
(2)解：当O运动到AC中点时，四边形AECF是矩形．证明： ∵CE平分∠ACB，CF平分∠BCA的外角，∴∠ECF＝∠ECA＋∠FCA＝90°.由(1)得OE＝OF，又∵O为AC的中点，∴AO＝CO.∴四边形AECF是平行四边形．又∵∠ECF＝90°，∴四边形AECF是矩形．
解：(3)当△ABC是直角三角形，即∠ACB＝90°时，在(2)的条件下，四边形AECF是正方形．
【点拨】本题综合考查矩形、正方形的判定
如图所示，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连结AE、CF.(1)求证：AF＝CE；(2)若AC＝EF，试判断四边形AFCE是什么样的四边形，并证明你的结论
扎实基础 强化训练提高能力 中考必胜