



还剩6页未读,
继续阅读
中考数学专题复习 之 函数实际应用型问题课件PPT
展开
这是一份中考数学专题复习 之 函数实际应用型问题课件PPT
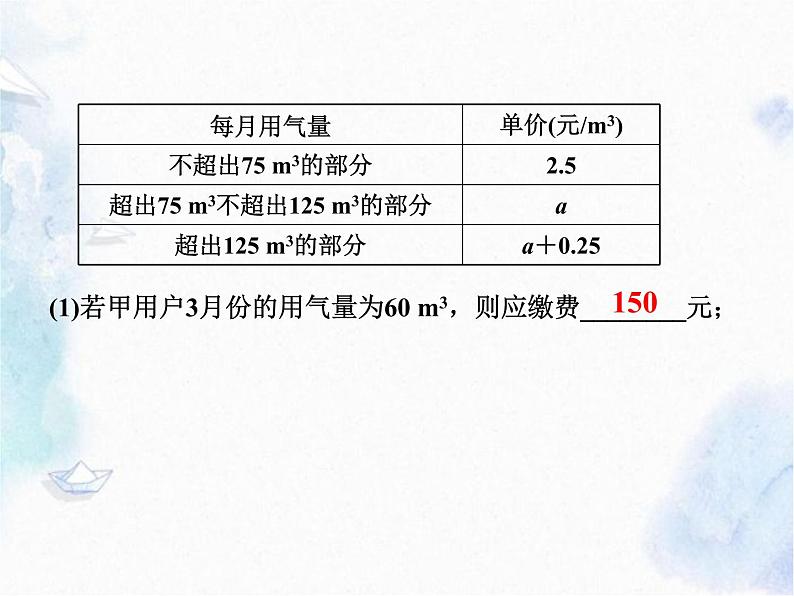
函数实际应用型问题 中考数学专题复习 函数实际应用型问题是把题中数量关系抽象为函数模型,如一次函数、二次函数、反比例函数以及它们的分段函数,进而应用函数进行分析、研究、解决有关问题. 函数问题的实质是研究两变量之间的对应关系,用函数思想构建数学模型解决实际问题. 函数实际应用型问题 探究一 分段函数实际应用 例1 为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如下表所示: (1)若甲用户3月份的用气量为60 m3,则应缴费________元;(2)若调价后每月支出的燃气费为y(元),每月的用气量x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;(3)在(2)的条件下,若乙用户2、3月份共用天然气175 m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?(1)若甲用户3月份的用气量为60 m3,则应缴费________元;150(2)若调价后每月支出的燃气费为y(元),每月的用气量x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;【例题分层分析】图中折线分为哪几段?②折线图中线段OA,线段AB,射线BC,它们的自变量分别对应②表中哪部分?③你能确定点A的坐标吗?A(75,75×2.5)即A(75,187.5)④你能根据A、B两点坐标求出a值吗?a=(325-187.5) ÷(125-75) =2.75 设线段OA的解析式为y1 = k1x,则有187.5 = 75k1∴k1 = 2.5 ∴线段OA的解析式为y1 = 2.5x(0≤x≤75)⑤如何确定线段OA,线段AB,射线BC的解析式?设线段AB的解析式为y2 = k2x+b1,由图象得187.5=75 k2 +b1325=125k2 +b1∴线段AB的解析式为y2 = 2.75x-18.75(75<x≤125)(385-325)÷3 = 20,故C(145,385)设射线BC的解析式为y3 = k3x+b2,由图象得325=125k3 + b2385=145k3 + b2∴射线BC的解析式为y3 = 3x-50(x>125)k2 = 2.75b1= - 18.75k3 = 3b2= - 50∴∴综上: 2.5x (0≤x≤75)y= 2.75x-18.75 (75<x≤125) 3x-50 (x>125)(3)在(2)的条件下,若乙用户2、3月份共用天然气175 m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?【例题分层分析】设乙用户2月份用气x m3,则3月份用气(175-x) m3, 问:2月份的用气量可以分布在哪几个区间?如果2月份的用气量在第3区间,那么3月份的用气量可以在@ 哪几个区间?如果2月份的用气量在第2区间,那么3月份的用气量可以在@ 哪几个区间?解:(3)设乙用户2月份用气x m3,则3月份用气(175-x) m3当x>125,175-x ≤ 75时 3x-50+2.5(175-x)=455解得x=135,175-135=40,符合题意;当75<x ≤ 125,175-x ≤ 75时 2.75x-18.75+2.5(175-x)=455解得x=145,不符合题意,舍去;当75<x≤125 ,75<175-x≤125时2.75x-18.75+2.75(175-x)-18.75=455,此方程无解.∴乙用户2、3月份的用气量分别是135 m3,40 m3. 解题方法点析 解分段函数问题的一般策略: (1)分段函数的特征:不同的自变量区间所对应的函数式不同,其函数图象是一个折线,解决分段函数问题,关键是要与所在的区间相对应. (2)分段函数中“折点”既是两段函数的分界点,同时又分别在两段函数上,求解析式时要用好“折点”坐标,同时在分析图象时还要注意“折点”表示的实际意义,“折点”的纵坐标通常是不同区间的最值.
函数实际应用型问题 中考数学专题复习 函数实际应用型问题是把题中数量关系抽象为函数模型,如一次函数、二次函数、反比例函数以及它们的分段函数,进而应用函数进行分析、研究、解决有关问题. 函数问题的实质是研究两变量之间的对应关系,用函数思想构建数学模型解决实际问题. 函数实际应用型问题 探究一 分段函数实际应用 例1 为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如下表所示: (1)若甲用户3月份的用气量为60 m3,则应缴费________元;(2)若调价后每月支出的燃气费为y(元),每月的用气量x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;(3)在(2)的条件下,若乙用户2、3月份共用天然气175 m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?(1)若甲用户3月份的用气量为60 m3,则应缴费________元;150(2)若调价后每月支出的燃气费为y(元),每月的用气量x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;【例题分层分析】图中折线分为哪几段?②折线图中线段OA,线段AB,射线BC,它们的自变量分别对应②表中哪部分?③你能确定点A的坐标吗?A(75,75×2.5)即A(75,187.5)④你能根据A、B两点坐标求出a值吗?a=(325-187.5) ÷(125-75) =2.75 设线段OA的解析式为y1 = k1x,则有187.5 = 75k1∴k1 = 2.5 ∴线段OA的解析式为y1 = 2.5x(0≤x≤75)⑤如何确定线段OA,线段AB,射线BC的解析式?设线段AB的解析式为y2 = k2x+b1,由图象得187.5=75 k2 +b1325=125k2 +b1∴线段AB的解析式为y2 = 2.75x-18.75(75<x≤125)(385-325)÷3 = 20,故C(145,385)设射线BC的解析式为y3 = k3x+b2,由图象得325=125k3 + b2385=145k3 + b2∴射线BC的解析式为y3 = 3x-50(x>125)k2 = 2.75b1= - 18.75k3 = 3b2= - 50∴∴综上: 2.5x (0≤x≤75)y= 2.75x-18.75 (75<x≤125) 3x-50 (x>125)(3)在(2)的条件下,若乙用户2、3月份共用天然气175 m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?【例题分层分析】设乙用户2月份用气x m3,则3月份用气(175-x) m3, 问:2月份的用气量可以分布在哪几个区间?如果2月份的用气量在第3区间,那么3月份的用气量可以在@ 哪几个区间?如果2月份的用气量在第2区间,那么3月份的用气量可以在@ 哪几个区间?解:(3)设乙用户2月份用气x m3,则3月份用气(175-x) m3当x>125,175-x ≤ 75时 3x-50+2.5(175-x)=455解得x=135,175-135=40,符合题意;当75<x ≤ 125,175-x ≤ 75时 2.75x-18.75+2.5(175-x)=455解得x=145,不符合题意,舍去;当75<x≤125 ,75<175-x≤125时2.75x-18.75+2.75(175-x)-18.75=455,此方程无解.∴乙用户2、3月份的用气量分别是135 m3,40 m3. 解题方法点析 解分段函数问题的一般策略: (1)分段函数的特征:不同的自变量区间所对应的函数式不同,其函数图象是一个折线,解决分段函数问题,关键是要与所在的区间相对应. (2)分段函数中“折点”既是两段函数的分界点,同时又分别在两段函数上,求解析式时要用好“折点”坐标,同时在分析图象时还要注意“折点”表示的实际意义,“折点”的纵坐标通常是不同区间的最值.
相关课件
中考数学函数的实际应用问题课件PPT: 这是一份中考数学函数的实际应用问题课件PPT,共23页。
中考数学-函数的实际应用问题课件PPT: 这是一份中考数学-函数的实际应用问题课件PPT,共43页。
初中数学中考复习 专题复习(五) 函数的实际应用题课件PPT: 这是一份初中数学中考复习 专题复习(五) 函数的实际应用题课件PPT,共59页。












