全等三角形复习 中考研讨课课件

这是一份全等三角形复习 中考研讨课课件
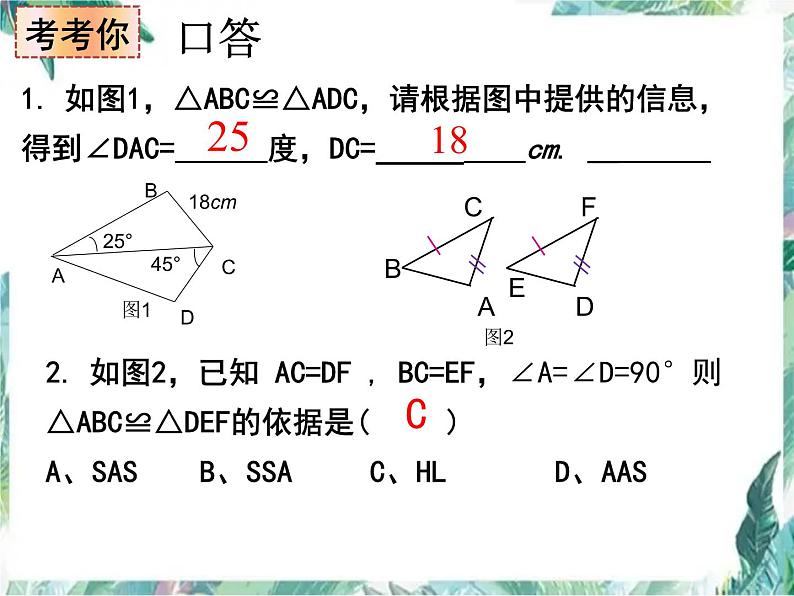
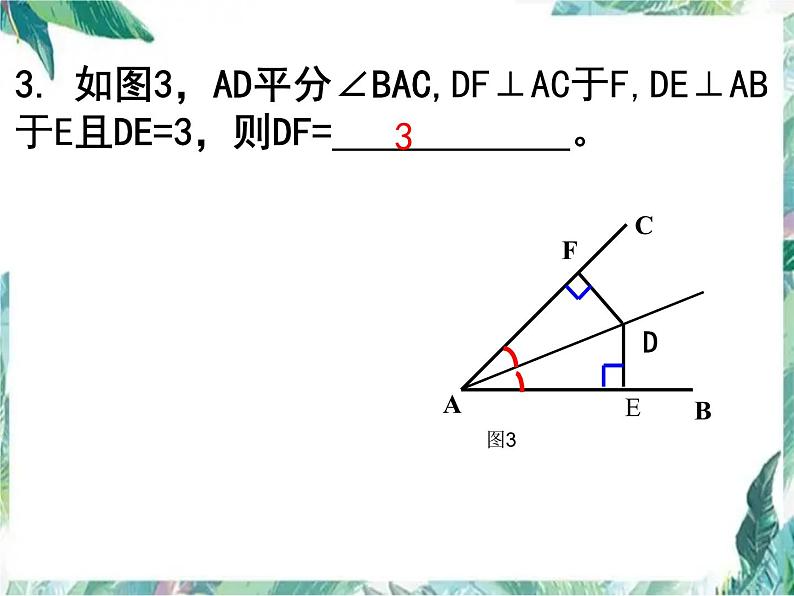
全等三角形复习课2022/4/25中考数学复习研讨课1. 如图1，△ABC≌△ADC，请根据图中提供的信息， 得到∠DAC= 度，DC= cm. 　 18　口答25 2. 如图2，已知 AC=DF , BC=EF，∠A=∠D=90°则△ABC≌△DEF的依据是( )A、SAS B、SSA C、HL D、AASC考考你3. 如图3，AD平分∠BAC,DF⊥AC于F,DE⊥AB于E且DE=3，则DF= 。3定义:能够完全重合的两个三角形叫做全等三角形。性质判定三角形全等知识梳理1.对应边相等，对应角相等．2.对应线段（角平分线、中线、高线、中位线）相等，对应周长相等，对应面积相等．1.一般三角形：SSS、SAS、AAS、ASA2.仅适用于直角三角形：HL3.传递性20　走进中考1.（2013柳州）如图1，△ABC ≌△DEF，请根据图中提供的信息，写出x=　 ．2.如图2，已知 AC=BD,请你添加1个条件 使△ ABC ≌△ BADBC=AD或∠CAB=∠DBA3．如图3，某同学把一块三角形状的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是(　　)．A．带①去 D．带③去B．带②去C．带① ②去4. 如图4，在△ABC和△FED 中，已知∠C=∠D，∠B=∠E，要判定这两个三角形全等，还需要条件（ ） A.AB=ED B.AB=FD C.AC=DF D.∠A=∠F CD图3全等三角形常见模型可看成是由对应相等的边在同一边上移动所构成，故对应点的相等关系一般可由同一直线上线段的和或差证得图形沿某一直线对称，且这条直线两边的部分能完全重合，重合的顶点就是全等三角形的对应点可看成由三角形某一个顶点为中心旋转构成，故一般有一对相等的角隐含在平行线、对顶角、某些角的和或差中也叫双直角三角形，其中的证明多数可以用到同（等）角的余角相等这个定理，相等的角就是对应的角注：AC=BC,CD=CE,∠ACB=∠DCE1.（2016•金华）如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC ≌△BAD的是（　　）A. AC=BD B. ∠CAB=∠DBA C. ∠C=∠D D. BC=ADA变式：如图2，已知 AD=BC,请你添加1个条件 使△ ABC ≌△ BADBC=AD或∠CBA=∠DAB3. 如图5，在Rt△ABC中，∠C＝900，AD平分∠BAC交BC于D， D E⊥AB于E,若AC=6，BC=8，CD=3，AB= ,DE= ,S △ADB= 。10　3　15　2.(安顺)如图5，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定ADF≌△CBE的是（ ) A．∠A=∠C B. AD=CB C. BE=DF D. AD∥BCB　 如图1，在△ABC中，AD⊥BC于D, AD=BD，F是AD上一点且DF=DC.点拨：全等是证明两条线段相等或角等常用方法之一理由如下:∵ AD ⊥BC于D ∴ ∠BDF=∠ADC=90°又∵ AD=BD DF=DC∴△ DBF ≌△ DAC （SAS）∴BF=AC（1）BF=AC∵ △ DBF ≌△ DAC∴ ∠FBD=∠CAD又∵ ∠1=∠2 ∴ ∠AEF=∠BDF=90°即BF⊥AC 于点E延长BF交AC于E 挑战中考(2)BF、AC所在的直线有怎样的位置关系？请说明理由.（2）BF ⊥AC求证：△DBF ≌△DAC(1)BF和AC有怎样的大小关系？说明理由.则BF和AC有怎样的关系？请说明理由.ABDCF如图3，在上题中，其它条件不变，若连接CF将△DCF绕点D顺时针旋转一定的角度后，则BF与AC的关系是否发生变化呢？变式1ABDCF如图4，若将△DCF绕点D逆时针旋转一定的角度后，则BF与AC的关系呢？变式2拓展题将变式2中的等腰直角三角形△ABD 和△DCF都变成等边三角形，其它条件不变，则BF与AC的关系又如何？ BF与AC的夹角是多少度呢？如果将已知条件改为AD=BD,DC=DF, ∠ADB=∠FDC=n° ,则BF与AC的夹角是多少度呢？畅所欲言通过今天的学习,你有什么收获？www.czsx.com.cn作业必做题：中考宝典P73 14题选做题：中考宝典P73 16题