中考数学 特殊平行四边形 复习课 精品课件

这是一份中考数学 特殊平行四边形 复习课 精品课件，共21页。PPT课件主要包含了知识归纳，四个角都是直角，两条对角线相等，四条边都相等，cm或12cm，小练笔，3-2，例题讲解，活动四课堂小结，方程思想等内容，欢迎下载使用。
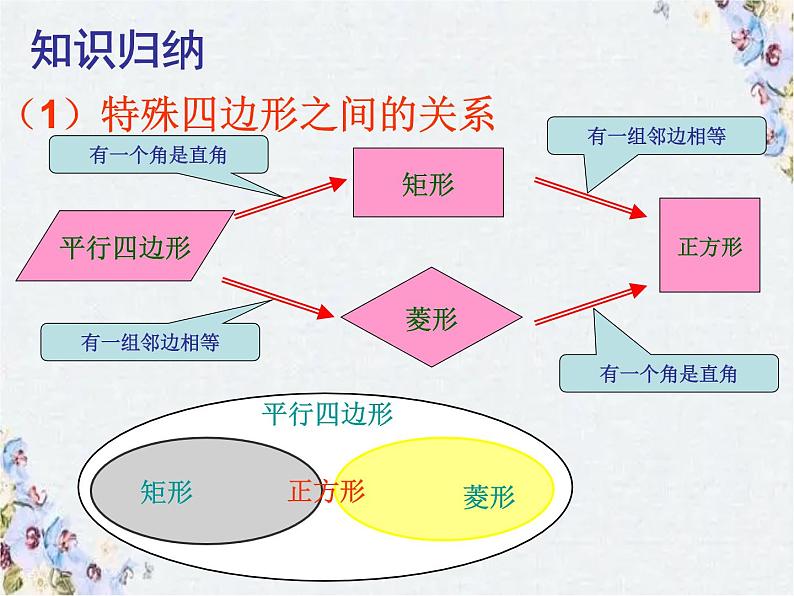
（1）特殊四边形之间的关系
（2）特殊平行四边形的性质
5、所有的平行四边形都是中心对称图形，其对称中心为对角线交点。
矩形、菱形和正方形具有平行四边形的所有性质
2、平行四边形的对边相等
3、平行四边形的对角相等
4、平行四边形的对角线互相平分
1、平行四边形的对边平行
是轴对称图形，有2条对称轴
互相垂直，每条对角线平分一组对角
是轴对称图形， 有4条对称轴
具有矩形和菱形的所有性质
具有平行四边形的一般性质
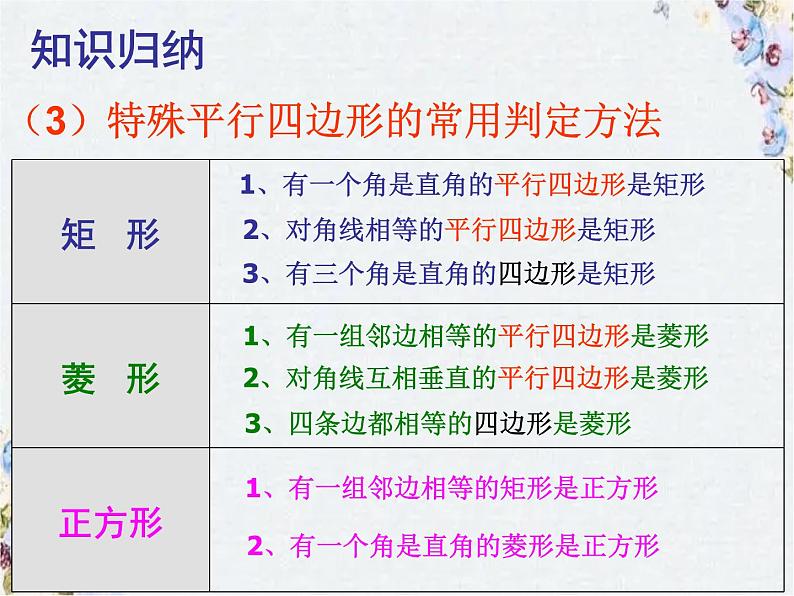
（3）特殊平行四边形的常用判定方法
1、有一个角是直角的平行四边形是矩形
3、有三个角是直角的四边形是矩形
2、对角线相等的平行四边形是矩形
1、有一组邻边相等的平行四边形是菱形
3、四条边都相等的四边形是菱形
2、对角线互相垂直的平行四边形是菱形
1、有一组邻边相等的矩形是正方形
2、有一个角是直角的菱形是正方形
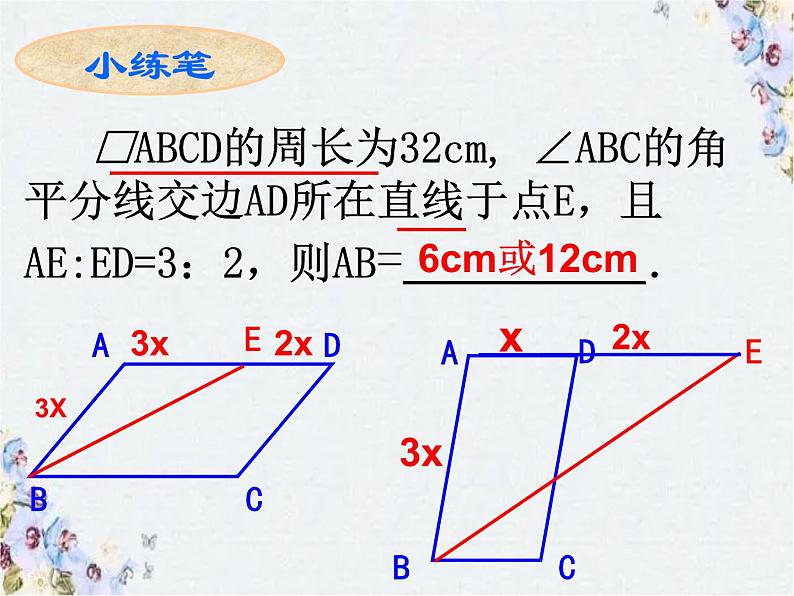
□ABCD的周长为32cm, ∠ABC的角平分线交边AD所在直线于点E，且AE:ED=3：2，则AB=___________．
1.如图，Rt△OAB的两条直角边在坐标轴上，已知点A（0，2），点B（3，0），则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为_________________。
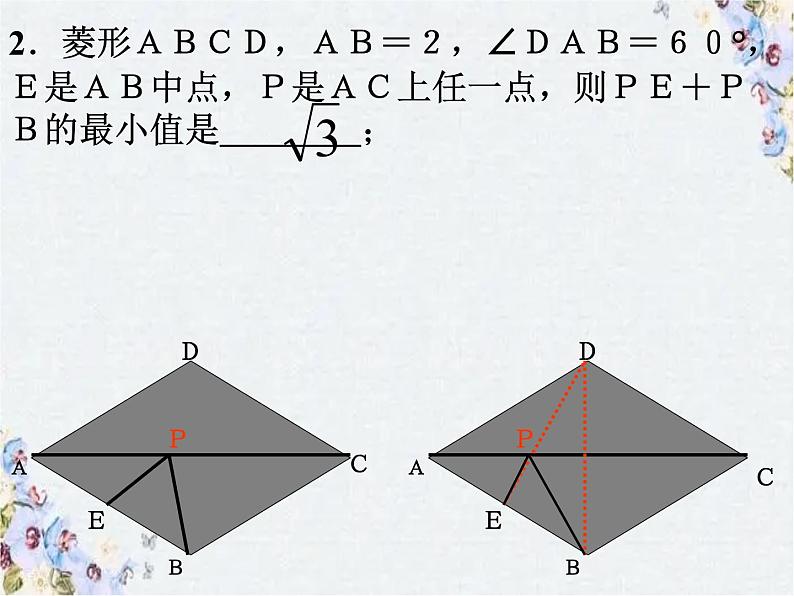
2．菱形ＡＢＣＤ，ＡＢ＝２，∠ＤＡＢ＝６０°，Ｅ是ＡＢ中点，Ｐ是ＡＣ上任一点，则ＰＥ＋ＰＢ的最小值是＿＿＿＿；
例1 如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN．（1）求证：四边形BMDN是菱形；
（2）若AB=4，AD=8，求MD的长．
例2 将两块全等的含30°角的三角尺如图1摆放在一起，设较短直角边为1．
(1)四边形ABCD是平行四边形吗？说出你的结论和理由．
(2)如图，将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置，四边形ABC1D1是平行四边形吗？说出你的结论和理由．
(3)在Rt△BCD沿射线BD方向平移的过程中，当点B的移动距离为______时，四边形ABC1D1为矩形，请说明理由；
(3)在Rt△BCD沿射线BD方向平移的过程中，当点B的移动距离为______时，四边形ABC1D1为菱形，请说明理由；
例3 如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．
（1）求证：EF=EG；
（1）证明： ∵∠GEB+∠BEF=90° ∠DEF+∠BEF=90° ∴∠DEF=∠GEB 又∵ED=BE ∴Rt△FED≌Rt△GEB， ∴EF=EG；
（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；
则EH=EI，∠HEI=90°∵∠GEH+∠HEF=90°∠IEF+∠HEF=90°∴∠IEF=∠GEH∴Rt△FEI≌Rt△GEH∴EF=EG
（2）成立．证明：过点E分别作BC、CD的垂线，垂足分别为H、I，
（3）解：过点E分别作BC、CD的垂线，垂足分别为M、N，则∠MEN=90°，∴EM∥AB，EN∥AD．∴△CEN∽△CAD，△CEM∽△CAB，
（3）如图3，将(2)中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b，求 的值．
∵∠NEF+∠FEM=∠GEM+∠FEM=90°，∴∠GEM=∠FEN，∵∠GME=∠FNE=90°，∴△GME∽△FNE，
3、特殊与一般的思想方法