中考数学 相似三角形复习课件PPT

这是一份中考数学 相似三角形复习课件PPT，共31页。PPT课件主要包含了知识梳理等内容，欢迎下载使用。
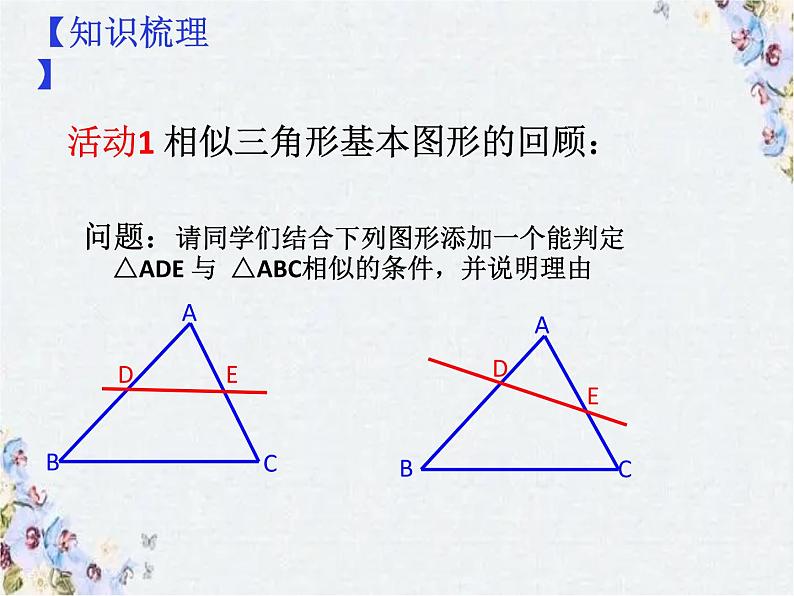
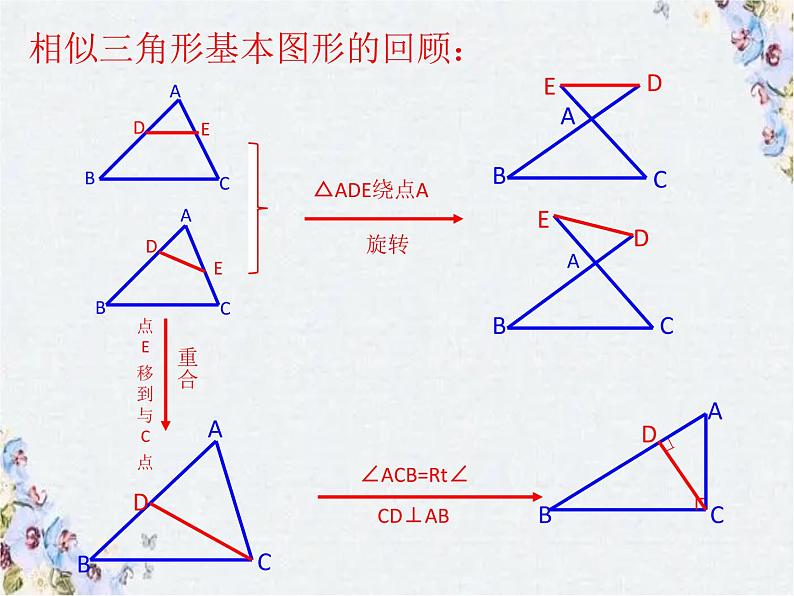
活动1 相似三角形基本图形的回顾：
问题：请同学们结合下列图形添加一个能判定△ADE 与 △ABC相似的条件，并说明理由
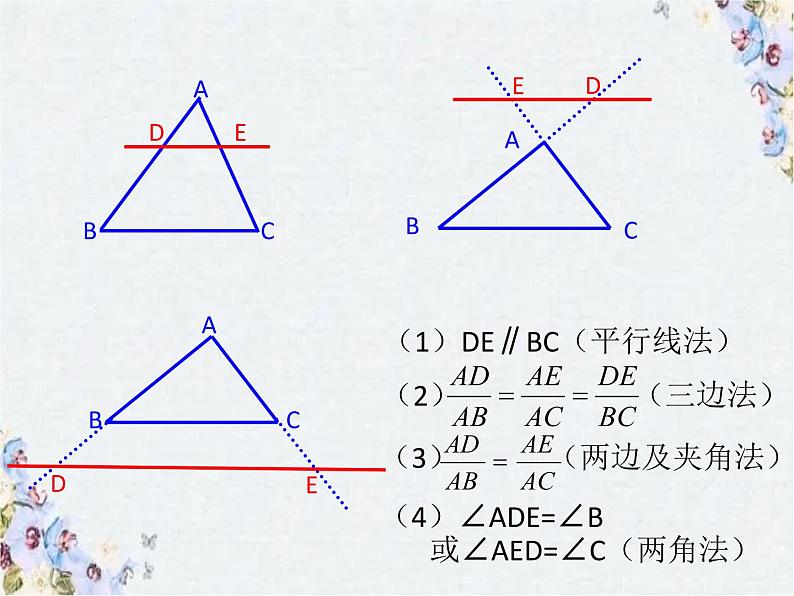
（1）DE∥BC（平行线法）
（4）∠ADE=∠B 或∠AED=∠C（两角法）
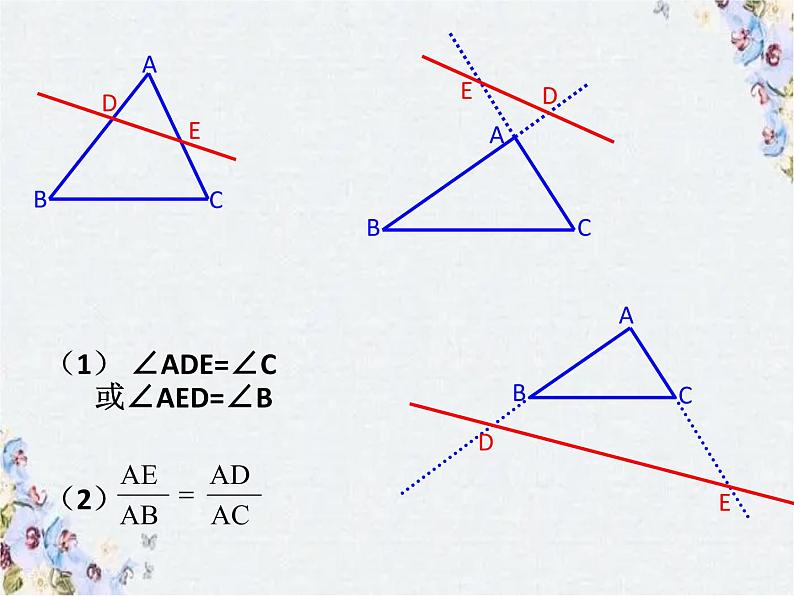
（1） ∠ADE=∠C 或∠AED=∠B
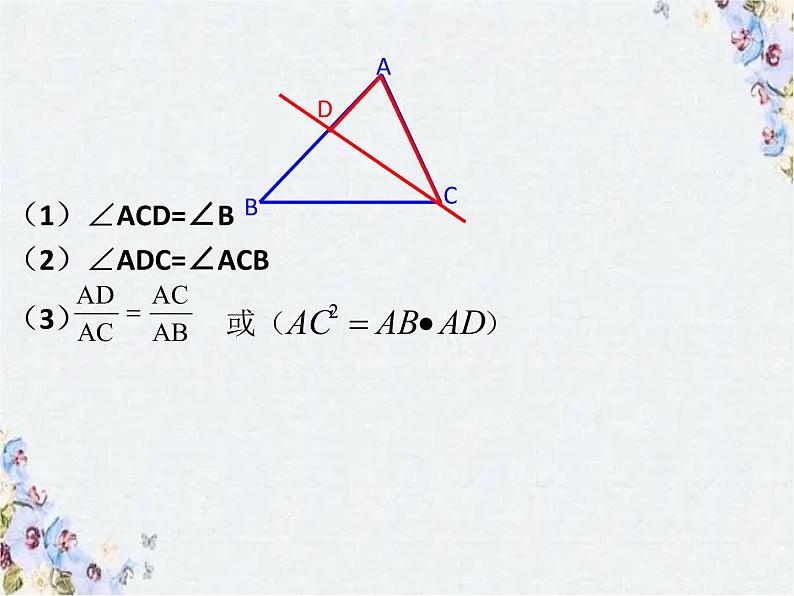
（1）∠ACD=∠B（2）∠ADC=∠ACB
相似三角形基本图形的回顾：
已知：如图所示：△ABC∽△DEF，AB=8，AC=10，DE=4，∠F=45°，∠B=75 °则∠E= ,DF= .
相似三角形的性质1：相似三角形对应角相等，对应边成比例。
已知：△ABC∽△DEF，它们的相似比为2:3，则△ABC与△DEF对应高的比为 ，周长的比 ，面积的比为 。
相似三角形的性质2：相似三角形对应高、对应中线、对应角平分线的比、周长的比等于相似比；相似三角形的面积的比等于相似比的平方。
相似三角形判定方法：1、平行三角形一边的直线和其它两边（或两边延长线）相交，所构成的三角形与原三角形相似（预备定理）
相似三角形判定方法：2、两角对应相等，两三角形相似。3、两组对应边成比例且夹角相等，两三角形相似。4、三组对应边成比例两三角形相似。5、斜边和一直角边对应成比例的两个直角三角形相似。
例题1.（2016年安徽，8,4分）如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段AC的长为（ ）
例2.如图在正方形ABCD中，E为AB边的中点，G，F分别为AD，BC边上的点，若AG=1，BF=2，∠GEF=90°，则正方形的边长为 。
变式：在等边△ABC中，D为BC边上的一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的边长为 。
例3.（1）已知正方形ABCD中，对角线AC与BD相交于点O，如图① ，将△BOC绕点O逆时针方向旋转得到△B′OC′，OC′与CD交于点M，OB′与BC交于点N，请猜想线段CM与BN的数量关系，并证明你的猜想。（2）如图② ，将（1）中的△BOC绕点B逆时针旋转得到△BO′C′，连接AO′、DC′，请猜想线段AO′与DC′数量关系，并证明你的猜想。（3）如图③ ，已知矩形ABCD和Rt△AEF有公共点A，且∠AEF=90°，∠EAF=∠DAC=α，连接DE、CF，
活动2：如图1中△ADE∽△ABC，相似比为2:3（1）△ADE和△ABC对应中线的比 ，对应角平分线的比 ，对应高的比 。（2）若它们的周长差为10，则△ADE和△ABC的周长分别是 和 。（3）若它们的面积和为19.5，则△ADE和△ABC的面积分别是 和 。
总结相似三角形的性质：
（1）相似三角形的对应中线比，对应角平分线比，对应高比都等于相似比；（2）相似三角形周长的比等于相似比；（3）相似三角形面积的比等于相似比平方。
相似在日常生活中应用举例
（山东济宁中考题）如图，放映幻灯时，通过光源，把幻灯片上的图形放大到屏幕上. 若光源到幻灯片的距离为20 cm,到屏幕的距离为60 cm,且幻灯片中图形的高度为6 cm，则屏幕上图形的高度为 cm．
位似定义：对于两个多边形不仅相似，如果它们的对应顶点的连线相交于一点，那么这两个多边形就是位似图形，这点叫做位似中心。
【典例精析】
例1：如图，下列条件①∠B=∠ACD；②∠ADC=∠ACB；③ ；④ 其中能判定△ABC∽△ACD的是 。
变式1：（2016杭州）如图，在△ABC中，点D、E分别在AB、AC上，∠AED=∠B.线段AG分别交线段DE、BC于点F、G且 （1）求证：△ADF∽△ACG（2）若 ，求 的值
变式2（山东泰安中考题）如图四边形ABCD中，AC平分∠DAB,∠ADC=∠ACB=900，E为AB的中点．(1) 求证：AC2=AB•AD；(2) 求证：CE∥AD；(3) 若AD=4，AB=6，求 的值．
例2：如图，正方形ABCD的边长为4，M，N分别是BC，CD上的两个动点，且始终保持AM⊥MN。当BM= 时，四边形ABCN的面积最大。
变式1：（2015岳阳）如图，在正方形ABCD中，M是BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N（1）求证：△ABM∽△EFA；（2）若AB=12，BM=5，求DE的长。
∵ABCD是正方形∴ ∠BAD =∠B =90°即∠1+ ∠2= 90° ∠2+ ∠3= 90°∴ ∠1= ∠3又∵EF ⊥AM∴ ∠AFN= ∠B =90°∴ △ABM ∽ △EFA
变式2：（扬州市中考题）已知矩形ABCD的一边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．（1）如图1，已知折痕与边BC交于点O，连接AP、OP、OA．①求证：△OCP∽△PDA；②若△OCP与△PDA的面积比为1:4，求边AB的长
∵ABCD是矩形∴ ∠C= ∠B =∠D=90 °又∵ ∠APO= ∠B =90 °∴ ∠2+ ∠3=90 °又∵ ∠1+ ∠2=90 °∴ ∠1= ∠3∴ △OCP ∽ △PDA
【课堂总结】通过本节课的学习，你有哪些收获？还有什么疑惑？
【当堂检测】
1、（2016湘西）如图，在△ABC中，DE∥BC，DB=2AD，△ADE的面积为1，则四边形DBCE的面积为 2、（山东省莱芜市）如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC,若 1:4, ( ) A. 1:16 B. 1:18 C. 1:20 D. 1:24
3、如图，已知等腰△ABC中，顶角∠A=36°，BD为∠ABC的平分线，则 的值等于( ) A. 　　　 B. 　　　 C.1 　　　D.
4、（甘肃省陇南市）如图，边长为1的正方形ABCD中，点E在CB延长线上，连接ED交AB于点F，AF=x（0.2≤x≤0.8），EC=y．则在下面函数图象中，大致能反映y与x之闻函数关系的是（　　）
5、如图，CD是⊙O的弦，AB是直径，且CD⊥AB，垂足为P，求证：
点拨：连接AC，BC 证△ACP∽ △CBP
【分层作业】
1、必做题：书本复习题27第3、7题2、选做题：（湖南永州中考题）如图，已知AB⊥BD，CD⊥BD(1)若AB=9，CD=4，BD=10，请问在BD上是否存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？若存在，求BP的长；若不存在，请说明理由；(2) 若AB=9，CD=4，BD=12，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；(3) 若AB=9，CD=4，BD=15，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；(4) 若AB=m，CD=n，BD= p，请问在m、n、p 满足什么关系时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点? 两个P点? 三个P点?