




初中数学人教版八年级下册18.1.2 平行四边形的判定授课课件ppt
展开
这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定授课课件ppt,共15页。PPT课件主要包含了平行四边形,对角线,对边平行,对边相等,对角相等,对角线互相平分,思考问题引入新知,证明连接BD,还有别的方法吗,几何语言等内容,欢迎下载使用。
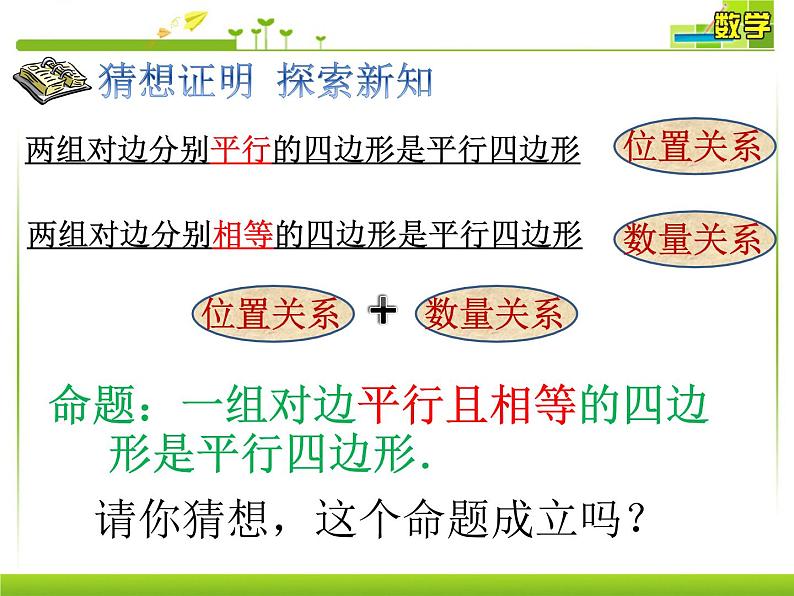
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,你能说出其中的道理吗?
2.会综合运用平行四边形的判定方法和性质证明问题。
1.掌握用一组对边平行且相等来判定平行四边形的方法;
请同学们猜想一下,如果只考虑四边形的一组对边,当它满足什么条件时这个四边形是平行四边形?
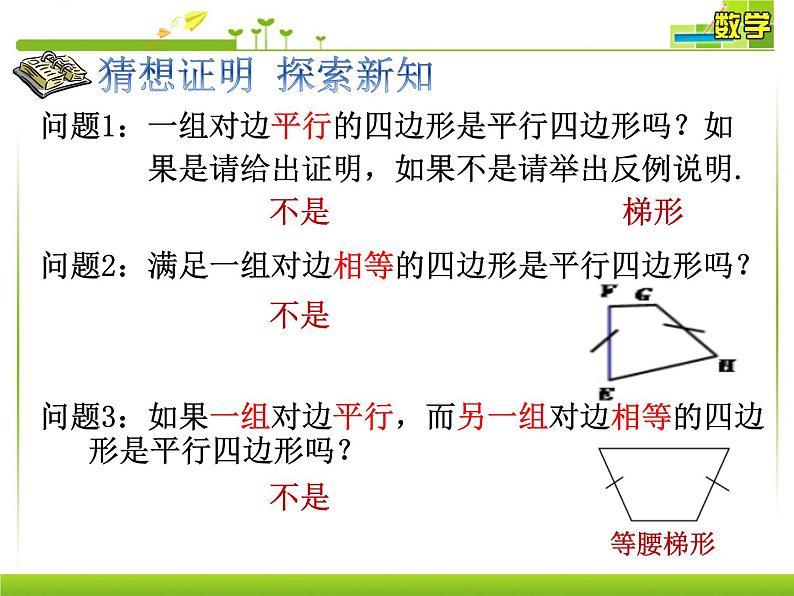
问题1:一组对边平行的四边形是平行四边形吗?如 果是请给出证明,如果不是请举出反例说明. Z```x``xk
问题2:满足一组对边相等的四边形是平行四边形吗?
问题3:如果一组对边平行,而另一组对边相等的四边 形是平行四边形吗?
请你猜想,这个命题成立吗?
命题:一组对边平行且相等的四边 形是平行四边形.
操作与探究:在方格纸中,做画一个满足一组对边平行且相等的四边形,并判断其是否是平行四边形.
命题:一组对边平行且相等的四边形是平行四边形.
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行 四边形
根据以上的证明你能概括出判定一个四边形是平行四边形的第五种方法吗?
平行四边形判定方法(5)
一组对边平行且相等的四边形是平行四边形.
强调:同一组对边平行且相等.
证明:∵四边形ABCD是平行四边形∴AB=CD,EB∥FD又EB= AB,FD= CD∴EB=FD∴四边形EBFD是平行四边形。
如图,在 ABCD中,E,F分别是AB,CD的中点.求证:四边形 EBFD是平行四边形.
在上题中,将“E,F分别是AB,CD的中点”改为“E,F分别是AB,CD上的点,且AE=CF”,结论是否仍然成立?请说明理由.
两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
从角考虑 两组对角分别相等的四边形是平行四边形.从对角线考虑 对角线互相平分的四边形是平行四边形.
判定一个四边形是平行四边形可从哪些角度思考?具体有哪些方法?
1、判断题:⑴相邻的两个角都互补的四边形是平行四边形. ( )⑵两组对角分别相等的四边形是平行四边形. ( )⑶一组对边平行,另一组对边相等的四边形是平行四边形 .( )⑷一组对边平行且相等的四边形是平行四边形. ( )⑸对角线相等的四边形是平行四边形. ( )⑹对角线互相平分的四边形是平行四边形 . ( )
2、如图, AC是□ABCD的一条对角线,BM⊥AC, ND⊥AC,垂足分别是M、N .求证:四边形BMDN是平行四边形.
相关课件
这是一份人教版八年级下册18.1.2 平行四边形的判定优秀课件ppt,共27页。PPT课件主要包含了你能证明吗,一组对应边相等,两组对边分别相等,证明连接AC,∵AD∥BC,∴∠DAC∠ACB,∴ΔABC≌ΔCDA,∴∠BAC∠ACD,∴AB∥CD,你还有其他证法吗等内容,欢迎下载使用。
这是一份人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定说课ppt课件,共18页。PPT课件主要包含了观察思考,三角形中有三条中位线,你能证明以上猜想吗,方法二,方法三,方法四,知识拓展,课堂小结,两层含义如图等内容,欢迎下载使用。
这是一份浙教版八年级下册4.4 平行四边形的判定多媒体教学ppt课件,共5页。










