初中数学18.2.1 矩形课文ppt课件

这是一份初中数学18.2.1 矩形课文ppt课件，共21页。PPT课件主要包含了平行四边形的性质，温故知新，一个角是直角，两组对边分别平行，情景创设，矩形的定义，生活中的实例，对边平行且相等，对角相等邻角互补，对角线互相平分等内容，欢迎下载使用。
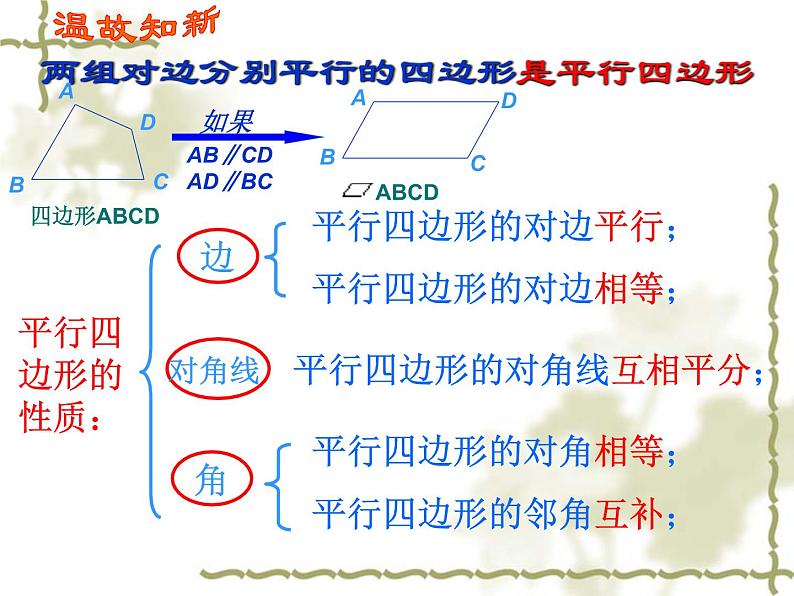
两组对边分别平行的四边形是平行四边形
平行四边形的对边平行；
平行四边形的对边相等；
平行四边形的对角相等；
平行四边形的邻角互补；
平行四边形的对角线互相平分；
我们已经知道平行四边形是特殊的四边形，因此平行四边形除具有四边形的性质外，还有它的特殊性质，同样对于平行四边形来说有特殊情况即特殊的平行四边形，这堂课我们就来研究一种恃殊的平行四边形——
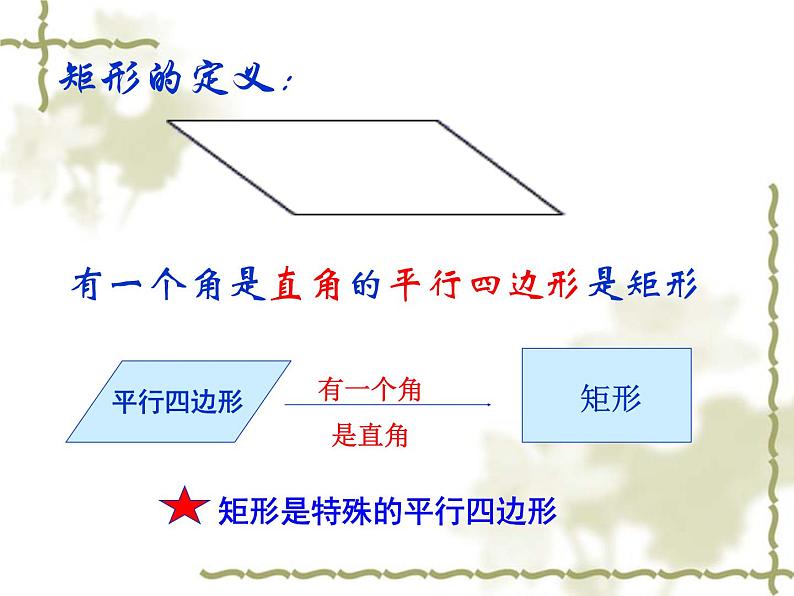
有一个角是直角的平行四边形是矩形
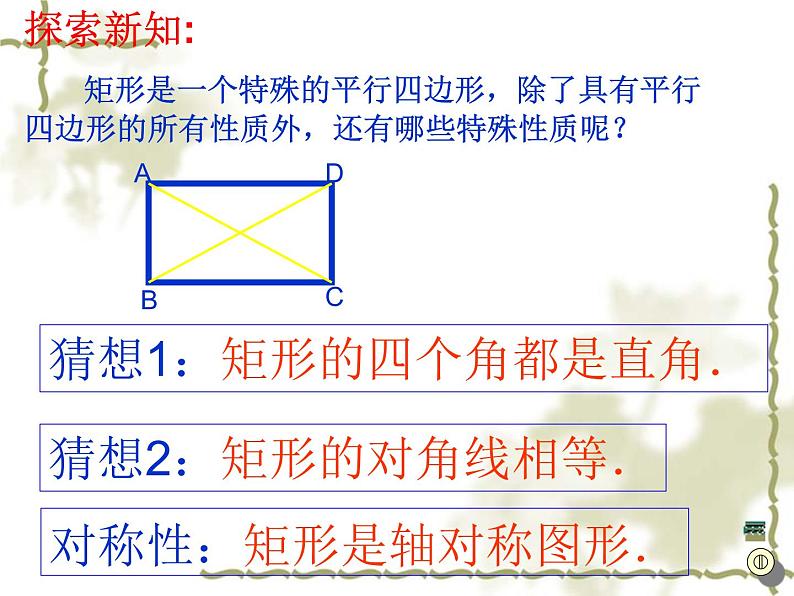
探索新知: 矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有哪些特殊性质呢？
猜想1：矩形的四个角都是直角．
猜想2：矩形的对角线相等．
对称性：矩形是轴对称图形．
已知：四边形ABCD是矩形, ∠A=900
求证：∠A= ∠B = ∠C=∠D=900
证明：∵ 四边形ABCD是矩形
∴ ∠A+ ∠B=1800
又∵ ∠A = ∠C， ∠B = ∠D（矩形的对角相等）
∴ ∠A= ∠B = ∠C=∠D=900
已知：四边形ABCD是矩形，求证：AC = BD
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB
　　2：矩形的对角线相等．
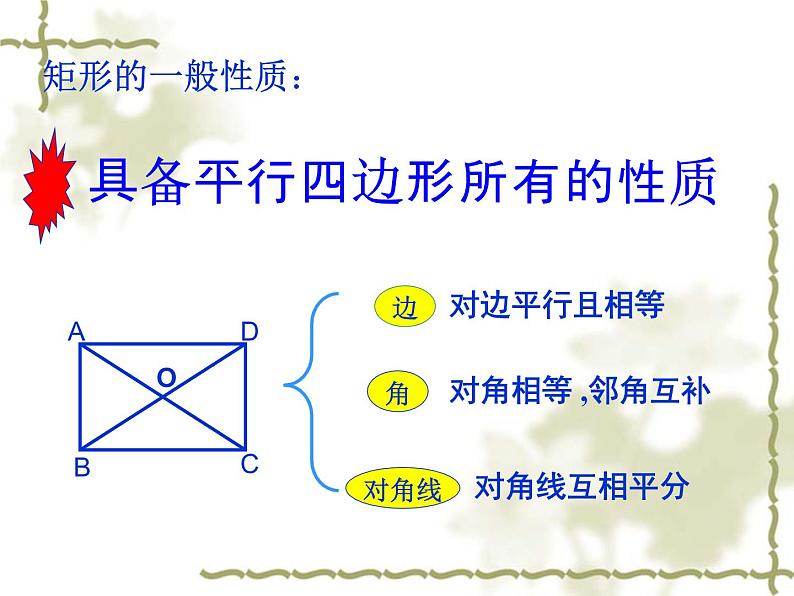
矩形的 两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形 的两条对角线相等
∵四边形ABCD是矩形
∴AD = BC ，CD = AB
∴AD ∥BC ，CD ∥AB
∴AO= CO ，OD = OB
公平,因为OA=OC=OB=OD
如图，在任意的矩形ABCD中，ＡＣ，ＢＤ相交于O，那么BO与AC有怎样的数量关关系？
Rt⊿ABC中，BO是一条什么线？ 由此你能得到什么结论？
直角三角形的性质： 直角三角形斜边上的中线等于斜边的一半。
在Rt三角形ABC中　　　　　　　　∵∠ABC=90°　 BO是AC边的中线　　　　　　　　　　　　　　　　　　　
已知：如左图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=4cm，求矩形对角线的长.
解：∵四边形ABCD是矩形，
∴AB=BO=4∴BD=2BO=2×4=8 ( cm ) .
∴△ABO为等边三角形，
∴AC=BD（矩形的对角线相等）.
1、已知四边形ABCD是矩形（1）若已知AB=8㎝，AD=6㎝， 则AC＝_______ ㎝ OB=_______ ㎝（2）若已知AC＝10㎝，BC=6㎝，则矩形的周长＝____ cm 矩形的面积＝_______ ㎝2 （3）若已知 ∠DOC=120°，AD＝6㎝，则AC= _____cm
2.已知△ABC是Rt△，∠ABC=900，BD是斜边AC上的中线
（1）若BD=3㎝则AC＝ ㎝（2）若∠C=30°，AB＝5㎝，则AC＝ ㎝， BD＝ ㎝，
3、如图，矩形ABCD被两条对角线分成四个小三角形的周长的和是86cm，对角线长是13cm，那么矩形的周长是多少？
4.如图,矩形的一条对角线长为8cm,两条对角线的一个交角为120°,求矩形的边长.
5、如图，在△ABC中，D，E，F，分别是BC、AC、AB边的中点，AH⊥BC于H，FD=8㎝，求HE的长
四个角都是直角 　　　　
互相平分相 等