平行四边形复习课 优秀课件

这是一份平行四边形复习课 优秀课件，共18页。

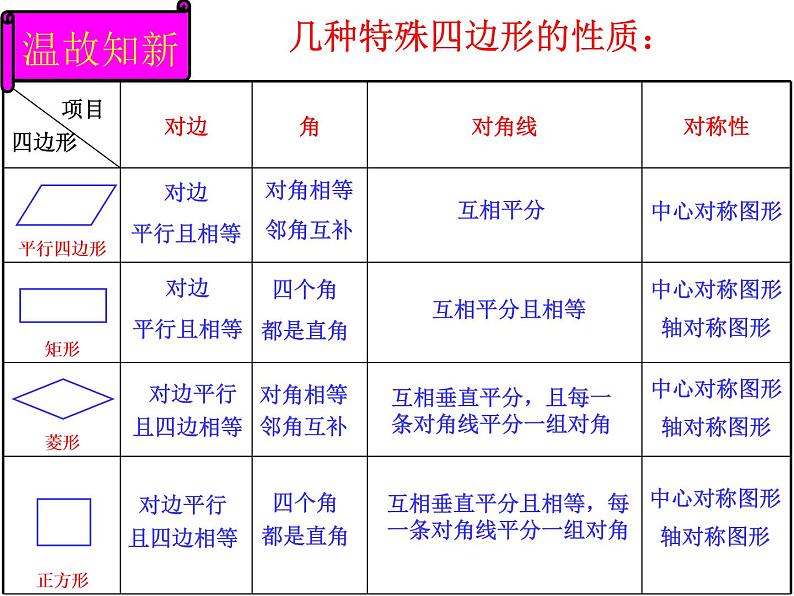
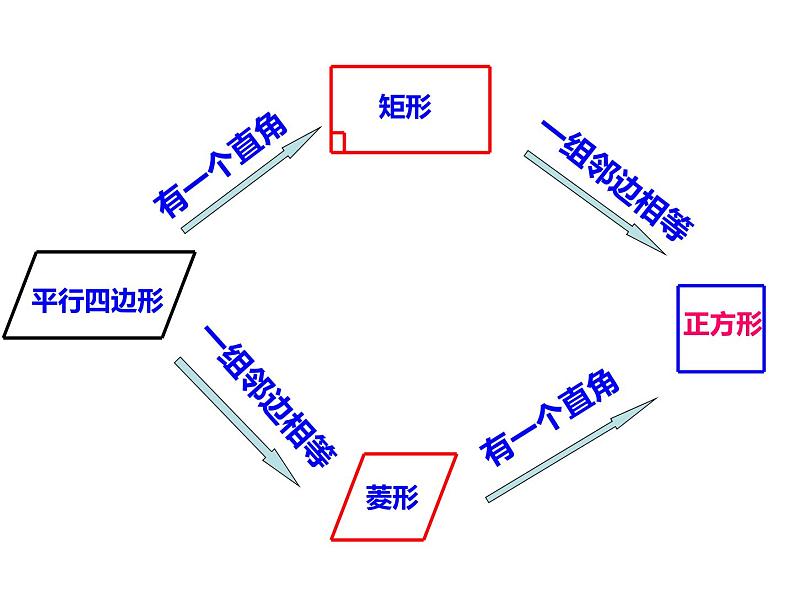
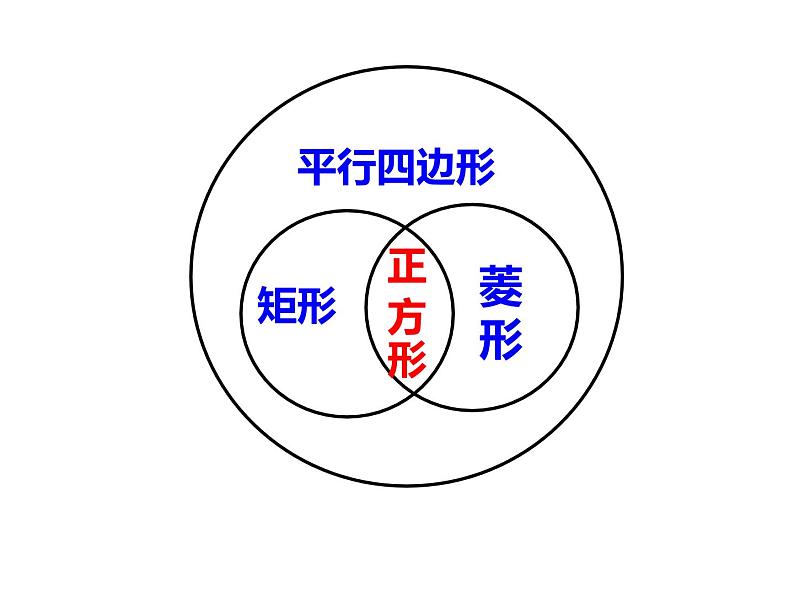
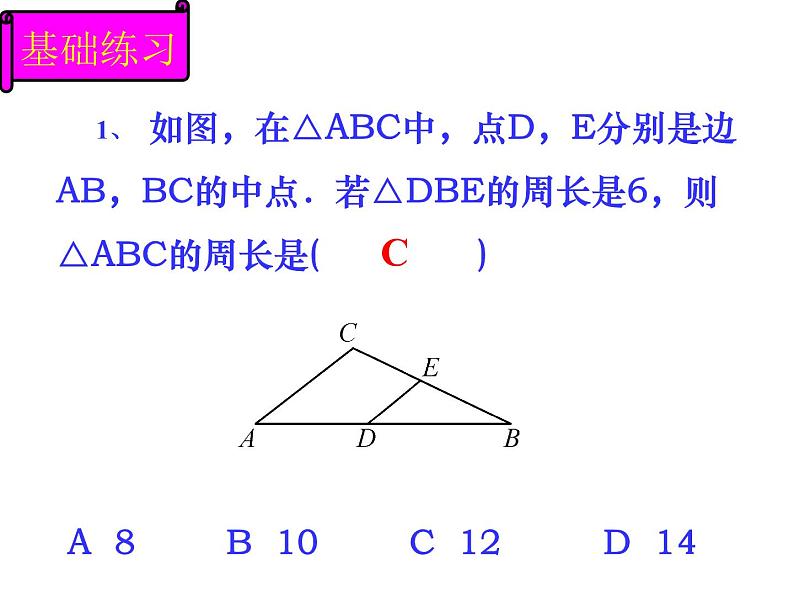
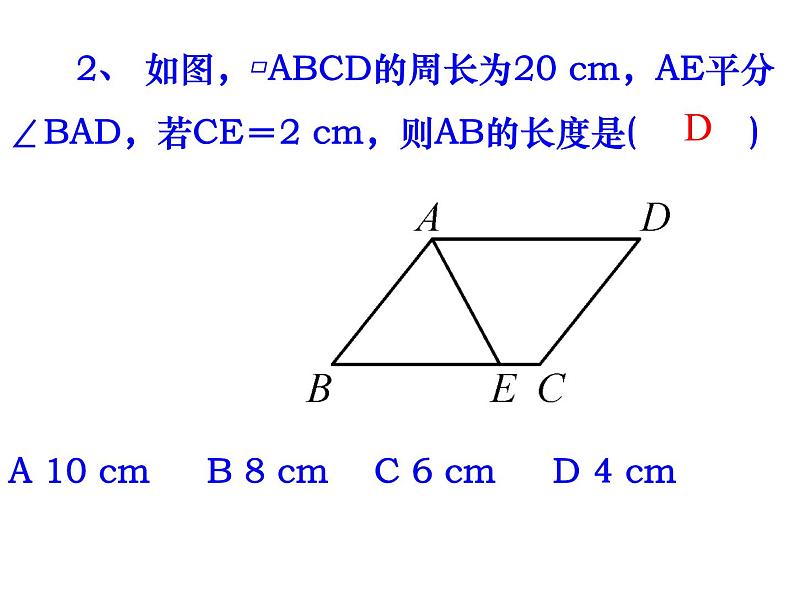
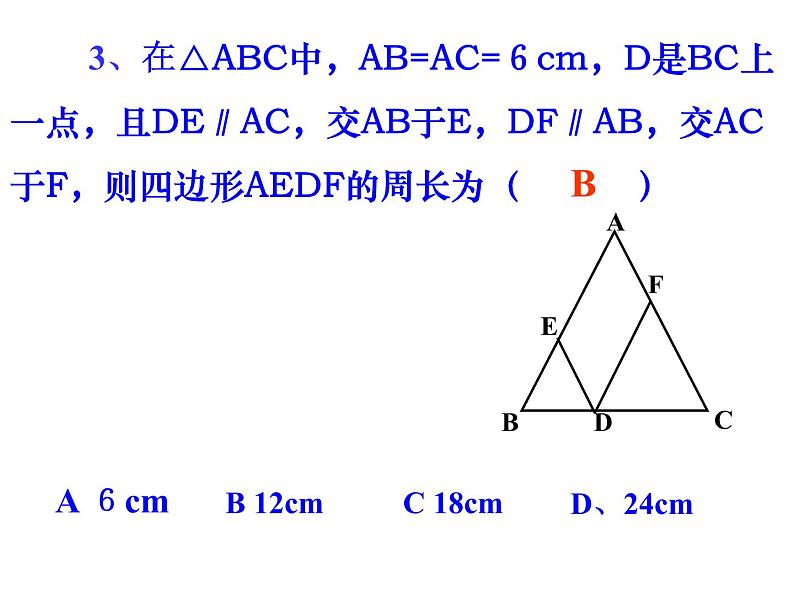
《平行四边形》复习课 对边平行且相等 对边平行且相等 对边平行且四边相等 对边平行且四边相等 对角相等 邻角互补 四个角都是直角对角相等邻角互补 四个角都是直角 互相平分互相平分且相等互相垂直平分，且每一条对角线平分一组对角互相垂直平分且相等，每一条对角线平分一组对角中心对称图形中心对称图形 轴对称图形中心对称图形 轴对称图形中心对称图形 轴对称图形 几种特殊四边形的性质：温故知新几种特殊四边形的常用判定方法：1、定义：两组对边分别平行 2、两组对边分别相等3、一组对边平行且相等 4、两组对角分别相等5、对角线互相平分1、定义：有一个角是直角的平行四边形 2、三个角是直角的四边形3、对角线相等的平行四边形1、定义：一组邻边相等的平行四边形 2、四条边都相等的四边形3、对角线互相垂直的平行四边形1、定义：一组邻边相等且有一个角是直角的平行四边形2、有一组邻边相等的矩形 3、有一个角是直角的菱形矩形菱形正方形平行四边形 1、 如图，在△ABC中，点D，E分别是边AB，BC的中点．若△DBE的周长是6，则△ABC的周长是( ) A 8 B 10 C 12 D 14C基础练习 2、 如图，▱ABCD的周长为20 cm，AE平分∠BAD，若CE＝2 cm，则AB的长度是( )A 10 cm B 8 cm C 6 cm D 4 cmD 3、在△ABC中，AB=AC=６cm，D是BC上一点，且DE∥AC，交AB于E，DF∥AB，交AC于F，则四边形AEDF的周长为（　　 ）B 4、矩形的对角线长为8，两对角线的夹角为60º，则矩形的两邻边分别长＿＿＿和＿＿＿. 4 5、 菱形的对角线长为6和8，则菱形的边长＿＿＿，面积是＿＿＿. 524 6、 菱形的周长等于高的8倍，则其最大内角等于（ ） A 60° B 90° C 120° D 150° DE 如图， ▱ABCD的对角AC,BD交于点O，过点B作BP//AC,过点C作CP//BD,BP与CP相交于点P，试判断四边形BPCO的形状，并说明理. 综合应用 追问1：若连接OP得四边形ABPO,它是什么四边形？ 追问2：若将▱ABCD改为矩形ABCD,其他条件不变，得到的四边形BPCO是什么四边形？ 追问3：若得到的四边形BPCO是矩形，应将▱ABCD改为什么四边形？ 追问4：能否得到正方形BPCO呢？此时四边形ABCD又是什么四边形？颗粒归仓 本节课你收获了什么？谢谢