初中鲁教版 (五四制)4 平行线的判定定理授课ppt课件

这是一份初中鲁教版 (五四制)4 平行线的判定定理授课ppt课件，共22页。PPT课件主要包含了谈谈收获等内容，欢迎下载使用。

公理 两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：同位角相等，两直线平行.
方法1： 内错角相等,两直线平行.方法2： 同旁内角互补，两直线平行.
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成： 内错角相等,两直线平行.
“行家” 看“门道”
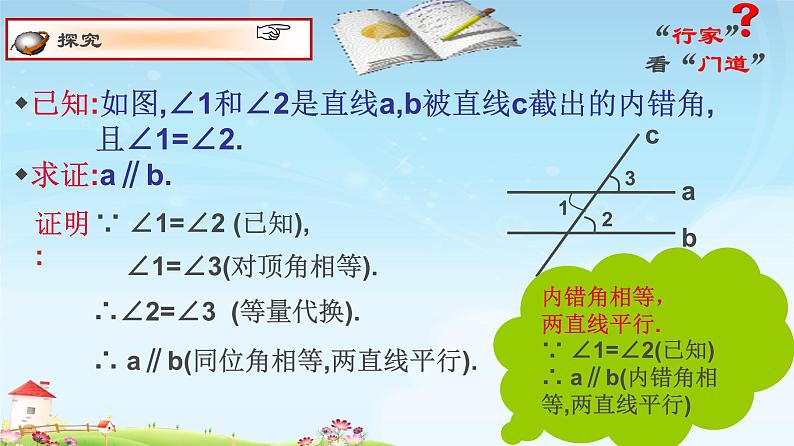
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角, 且∠1=∠2.求证:a∥b.
∵ ∠1=∠2 (已知),
∠1=∠3(对顶角相等).
∴∠2=∠3 (等量代换).
∴ a∥b(同位角相等,两直线平行).
内错角相等，两直线平行.∵ ∠1=∠2(已知)∴ a∥b(内错角相等,两直线平行)
公理 两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单说成：同旁内角互补，两直线平行.
已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.
∵ ∠1与∠2互补 (已知),
∴∠1+∠2=1800(互补的定义).
又∵∠3+∠2=1800 (平角的定义),
∴∠1=∠3(同角的补角相等).
∴ a∥b(同位角相等,两直线平行).
你还有其它的方法解决本题吗？
又∵∠4+∠2=1800 (平角的定义),
∴∠1=∠4(同角的补角相等).
∴ a∥b(内错角相等,两直线平行).
同旁内角互补，两直线平行.∵∠1+∠2=1800(已知)，∴ a∥b(同旁内角互补, 两直线平行).
巩固知识，拓展提高
1.如图，直线AB，CD与EF相交于G，H，下列条件：①∠1=∠2； ②∠3=∠6；③∠2=∠8； ④∠5+∠8=180°，其中能判定AB∥CD的是( )A.①③ B.①②④C.①③④ D.②③④
2.如图，下列推理是否正确？为什么？
(1) ∵∠1=∠2 ∴a∥b
(2)∵∠4+∠5=180° ∴c∥d
(3) ∵∠2=∠4 ∴c∥d
(4)∵∠3+∠6=180° ∴a∥b
如果∠ADE=∠ABC,则＿＿∥ ＿＿.
如果∠BCD=∠CBF,则＿＿∥ ＿＿.
如果∠DEC+∠BCE=1800,则＿＿∥ ＿ ＿.
DE BC
CD BF
DE BC
已知：如图，直线a,b被直线c所截， 且∠1+∠2=180°.求证：a∥b.
如图:(1)从∠1=∠4，可以推出　 ∥ ， 理由是 .
(2)从∠ABC +∠ =1800，可以推出AB∥CD ， 理由是 .
(3)从∠ =∠ ，可以推出AD∥BC， 理由是 .
(4)从∠5=∠ ，可以推出AB∥CD， 理由是 .
内错角相等，两直线平行
同旁内角互补,两直线平行
同位角相等,两直线平行
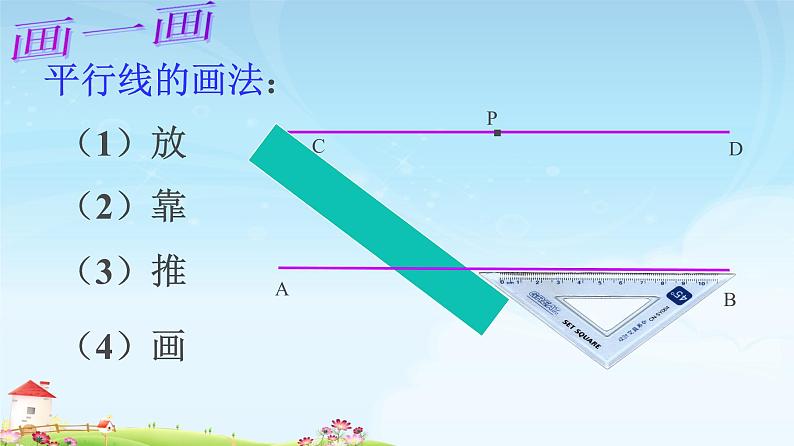
如图，木工师傅将厂用一把直尺画出两条平行的直线a和b，你知道这样做的道理吗？
在同一平面 ,垂直于同一条直线的两条直线互相平行.
如图，∠1=∠2=∠3，则直线l1、l2、l3的关系是________．
平行于同一直线的两直线平行.
l1 // l2 // l3
谈谈收获
1.能根据“同位角相等，两直线平行”证明“内错角相等，两直线平行”“同旁内角互补，两直线平行”，并能简单地应用这些结论. 2.初步了解证明的基本步骤和书写格式. 3.体会几何中推理的严谨性、书写的规范性，发展初步的演绎推理能力.
小明用下面的方法作出平行线，你认为他的作法对吗？为什么？通过这个操作活动,得到了什么结论?