2022年中考数学复习考点专题训练：反比例函数

这是一份2022年中考数学复习考点专题训练：反比例函数，共14页。试卷主要包含了反比例函数相关概念，反比例函数性质，反比例函数中的数形结合，反比例函数规律性问题，反比例函数K值几何意义，反比例函数的综合性问题等内容，欢迎下载使用。
考点一、反比例函数相关概念
1. 若函数y=mxm2−5是反比例函数，且它的图象在第一、三象限，则m的值为( )
A.2 B.−2C.6 D.−6
2.函数是反比例函数，则的值是（ ）
A．－1 B．－2 C．2 D．2或－2
3. 下列数表中分别给出了变量y与x之间的对应关系，其中是反比例函数关系的是( )
A.B.
C.D.
考点二、反比例函数性质
1．若点A（a﹣1，y1），B（a+1，y2）在反比例函数y（k＜0）的图象上，且y1＞y2，则a的取值范围是（ ）
A．a＜﹣1 B．﹣1＜a＜1 C．a＞1 D．a＜﹣1或a＞1
2．若点A（﹣1，y1），B（2，y2），C（3，y3）在反比例函数y的图象上，则y1，y2，y3的大小关系是（ ）
A．y1＞y2＞y3B．y2＞y3＞y1C．y1＞y3＞y2D．y3＞y2＞y1
3.在反比例函数图象上有两点A(x1，y1)、B(x2，y2)，x1＜0＜y1，y1＜y2，则m的取值范围是（ ）
A．m＞B．m＜ C．m≥D．m≤
4.已知y是x的反比例函数，当x＞0时，y随x的增大而减小．请写出一个满足以上条件的函数表达式 ．
考点三、反比例函数中的数形结合
1.反比例函数y＝与一次函数y＝ax+b在同一坐标系中的大致图象可能是（ ）
A．B．C．D．
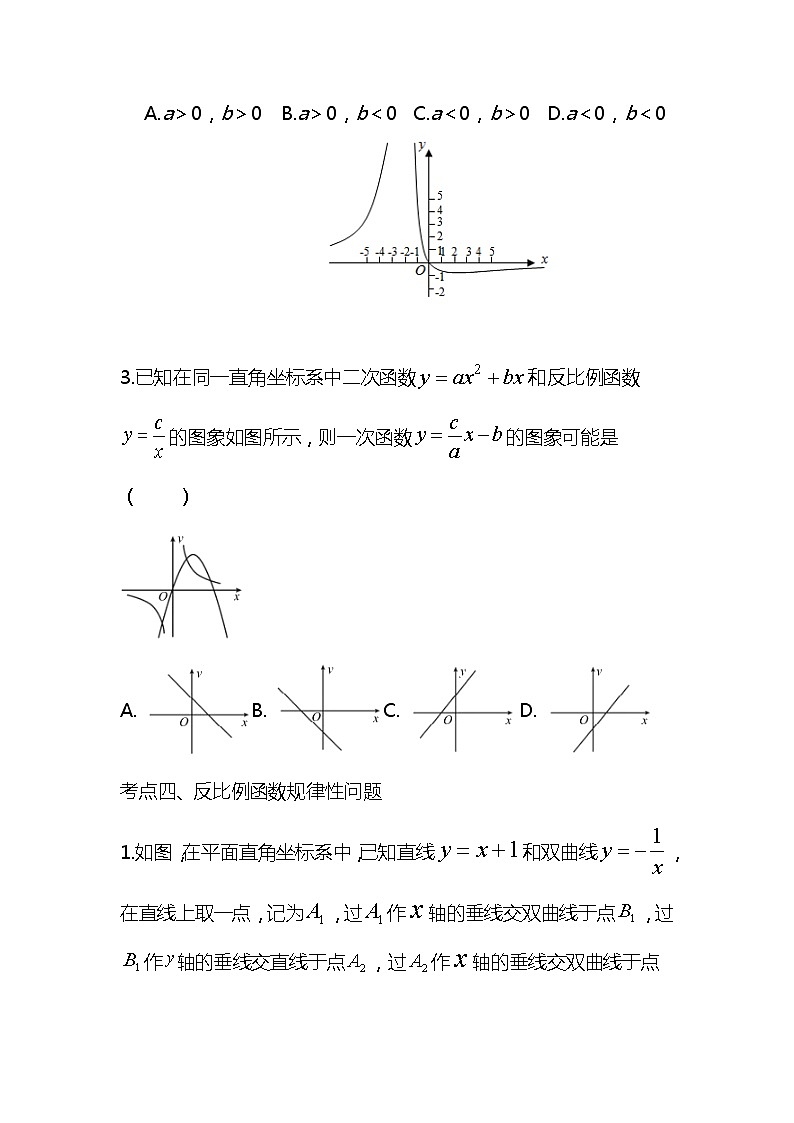
2.小明同学利用计算机软件绘制函数y＝（a、b为常数）的图象如图所示，由学习函数的经验，可以推断常数a、b的值满足（ ）
A.a＞0，b＞0 B.a＞0，b＜0C.a＜0，b＞0D.a＜0，b＜0

3.已知在同一直角坐标系中二次函数和反比例函数的图象如图所示，则一次函数的图象可能是（ ）
A. B. C. D.
考点四、反比例函数规律性问题
1.如图，在平面直角坐标系中，已知直线和双曲线，在直线上取一点，记为，过作轴的垂线交双曲线于点，过作轴的垂线交直线于点，过作轴的垂线交双曲线于点，过作轴的垂线交直线于点······，依次进行下去，记点的横坐标为，若则______．
2．如图，已知A1，A2，A3，…An，…是x轴上的点，且OA1＝A1A2＝A2A3＝…＝An﹣1An…＝1，分别过点A1，A2，A3，…，An，…作x轴的垂线交反比例函数y＝（x＞0）的图象于点B1，B2，B3，…，Bn，…，过点B2作B2P1⊥A1B1于点P1，过点B3作B3P2⊥A2B2于点P2…，记△B1P1B2的面积为S1，△B2P2B3的面积为S2…，△BnPnBn+1的面积为Sn，则S1+S2+S3+…+Sn等于（ ）
A．B．C．D．
考点五、反比例函数K值几何意义
1.如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=经过斜边OA的中点C，与另一直角边交于点D．若S△OCD=9，则S△OBD的值为 ．
2.如图，已知直线y=-x+2分别与x轴，y轴交于A，B两点，与双曲线y=交于E，F两点，若AB=2EF，则k的值是（ ）
A．-1B．1 C． D．
3.如图，OA在x轴上，OB在y轴上，OA＝4，OB＝3，点C在边OA上，AC＝1，⊙P的圆心P在线段BC上，且⊙P与边AB，AO都相切．若反比例函数y＝（k≠0）的图象经过圆心P，则k的值是（ ）
A．B．C．D．﹣2
4.如图，在平面直角坐标系中，▱ABCD的顶点B位于y轴的正半轴上，顶点C，D位于x轴的负半轴上，双曲线y=kx(k