2022年苏科版中考数学专题复习二次函数的性质与运用

2022年苏科版中考数学专题复习二次函数的性质与运用

一、单选题

1．抛物线y＝（x﹣1）2﹣2的顶点坐标为（　　）

A．（1，2） B．（1，﹣2）

C．（﹣1，2） D．（﹣1，﹣2）

2．将二次函数的图象平移后，得到二次函数的图象，平移的方法可以是（　　）

A．向左平移1个单位长度 B．向右平移1个单位长度

C．向上平移1个单位长度 D．向下平移1个单位长度

3．如图，已知抛物线（a，b，c为常数，）经过点，且对称轴为直线，有下列结论：

①；②；③；④无论a，b，c取何值，抛物线一定经过；⑤．其中正确结论有（　　）

A．1个 B．2个 C．3个 D．4个

4．如图，正方形OABC的边长为2，OC与y轴正半轴的夹角为30°，点A在抛物线 的图象上，则a的值为（　　） 

A． B． C． D．

5．已知点A（－2，y1），B（1，y2），C（3，y3）在二次函数图象上，则y1，y2，y3的大小关系是（          ）

A． B． C． D．

6．竖直向上发射的小球的高度 关于运动时间 的函数表达式为 ，其图象如图所示，若小球发射后第2秒与第6秒时的高度相等，则下列时刻中小球的高度最高的是（　　） 

A．第3秒 B．第3.5秒 C．第4秒 D．第6秒

7．如图，已知抛物线与直线交于，两点，则关于x的不等式的解集是（　　）

A．或

B．或

C．

D．

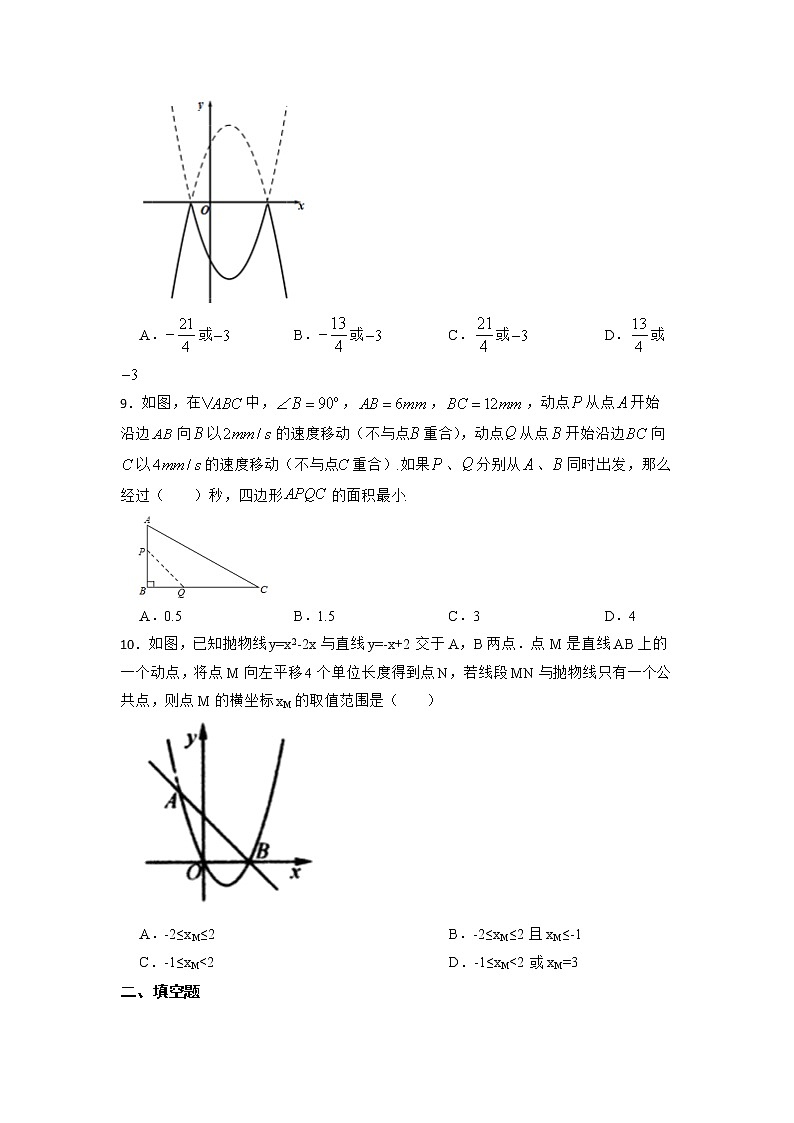
8．将二次函数的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示．当直线与新函数的图象恰有3个公共点时，b的值为（　　）

A．或 B．或 C．或 D．或

9．如图，在中，，，，动点从点开始沿边向以的速度移动（不与点重合），动点从点开始沿边向以的速度移动（不与点重合）.如果、分别从、同时出发，那么经过（　　）秒，四边形的面积最小.

A．0.5 B．1.5 C．3 D．4

10．如图，已知抛物线y=x2-2x与直线y=-x+2交于A，B两点．点M是直线AB上的一个动点，将点M向左平移4个单位长度得到点N，若线段MN与抛物线只有一个公共点，则点M的横坐标xM的取值范围是（　　） 

A．-2≤xM≤2 B．-2≤xM≤2且xM≤-1

C．-1≤xM<2 D．-1≤xM<2或xM=3

二、填空题

11．若是关于x的二次函数，则m=　     　．

12．将抛物线 向左平移2个单位，再向上平移3个单位后的抛物为　           　. 

13．矩形周长等于40，设矩形的一边长为 ，那么矩形面积 与边长 之间的函数关系式为　          　.  

14．如图，过点A(0，4)作平行于x轴的直线AC分别交抛物线与于B、C两点，那么线段BC的长是　     　．

15．已知二次函数y＝3（x﹣5）2，当x分别取x1，x2（x1≠x2）时，函数值相等，则当x＝时，函数值为 　     　．

16．如图，已知函数 与 的图象交于点 ，点 的纵坐标为1，则关于 的方程 的解为　     　. 

17．如图，在平面直角坐标系 xOy 中，已知 A 是抛物线 y=2x2+bx 上一点，顶点 B 的横坐标是1，当△AOB 是直角三角形时，点 A 的坐标为　                                 　．

18．已知二次函数（是常数，）的y与x的部分对应值如下表：

下列结论：

①；

②当时，函数最小值为；

③若点，点在二次函数图象上，则；

④方程有两个不相等的实数根．

其中，正确结论的序号是　     　．（把所有正确结论的序号都填上）

三、解答题

19．已知抛物线过点A（－1，0），B（0，6），对称轴为直线x＝1， 求该抛物线的解析式．

20．如图所示，已知二次函数的图象经过点 ， .当 时，求函数值. 

21．某民俗旅游村为接待游客住宿需要，开设了有100张床位的旅馆，当每张床位每天收费80元时，床位可全部租出，若每张床位每天收费提高10元，则相应的减少了10张床位租出，如果每张床位每天以10元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天应提高多少元？

22．如图是一个横断面为抛物线形状的拱桥，当水面宽（AB）为4m时，拱顶（拱桥洞的最高点）离水面2m．当水面下降1m时，求水面的宽度增加了多少？

23．已知二次函数 ．求证：不论 为何实数，此二次函数的图像与 轴都有两个不同交点．  

24．如图，是某座抛物线型的隧道示意图，已知路面AB宽24米，抛物线最高点C到路面AB的距离为8米，为保护来往车辆的安全，在该抛物线上距路面AB高为6米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离EF.（提示：以AB所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系）

25．某商家销售一款商品，该商品的进价为每件80元，现在的售价为每件145元，每天可销售40件商场规定每销售一件需支付给商场管理费5元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件若每件商品降价 元，每天的利润为 元，请完成以下问题的解答． 

（1）用含 的式子表示：①每件商品的售价为　          　元；②每天的销售量为　           　件；  

（2）求出 与 之间的函数关系式，并求出售价为多少时利润最大？最大利润是多少元？  

答案解析部分

1．【答案】B

2．【答案】B

3．【答案】B

4．【答案】D

5．【答案】D

6．【答案】C

7．【答案】C

8．【答案】A

9．【答案】B

10．【答案】D

11．【答案】1

12．【答案】

13．【答案】

14．【答案】2

15．【答案】0

16．【答案】

17．【答案】 或 或

18．【答案】①③④

19．【答案】解：设抛物线的解析式为y=a（x-1）²+b将A，B点坐标带入得，

解得a=-2，b=8，

则y=-2(x-1)²+8.

20．【答案】解：设该二次函数的解析式为 ， 

把点 ， 代入解析式，可得：

，

解得 ，

∴该二次函数的解析式为 ，

当 时， .

21．【答案】解：设每张床位提高x个10元，每天收入为y元．

则有y＝（80+10x）（100﹣10x）

＝﹣100x2+200x+8000．

当x＝﹣ ＝1时，可使y有最大值．

则x＝1时，y＝8100，

答：每张床位每天应提高10元．

22．【答案】解：建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，则通过画图可得知O为原点，

抛物线以y轴为对称轴，且经过A，B两点，OA和OB可求出为AB的一半2米，抛物线顶点C坐标为（0，2），

设顶点式y＝ax2+2，代入A点坐标（﹣2，0），

得出：a＝﹣0.5，

所以抛物线解析式为y＝﹣0.5x2+2，

当水面下降1米，通过抛物线在图上的观察可转化为：

当y＝﹣1时，对应的抛物线上两点之间的距离，也就是直线y＝﹣1与抛物线相交的两点之间的距离，

可以通过把y＝﹣1代入抛物线解析式得出：

﹣1＝﹣0.5x2+2，

解得：x＝± ，

所以水面宽度增加了（2 ﹣4）米．

23．【答案】解： ，不论 为何值时，都有 ，此时二次函数图象与 轴有两个不同交点．   

24．【答案】解：设

求出

写出解析式

把 代入求出 ，写出点 、 的坐标

25．【答案】（1）（145−x）；（40＋2x）

（2）根据题意可得：y＝（145−x−80−5）（2x＋40），＝−2x2＋80x＋2400，＝−2（x−20）2＋3200， 

∵a＝−2＜0，

∴函数有最大值，

∴当x＝20时，y有最大值为3200元，此时售价为145−20＝125元，

∴售价为125元时利润最大，最大利润是3200元．