小学数学冀教版四年级下册九 探索乐园教学课件ppt

这是一份小学数学冀教版四年级下册九 探索乐园教学课件ppt，共19页。PPT课件主要包含了学习目标，情景导入，探索新知，典题精讲，学以致用，课堂小结等内容，欢迎下载使用。
1.了解多边形及多边形的内角概念。2.通过不同方法探索多边形的内角和 公式，并会利用它进行有关计算。
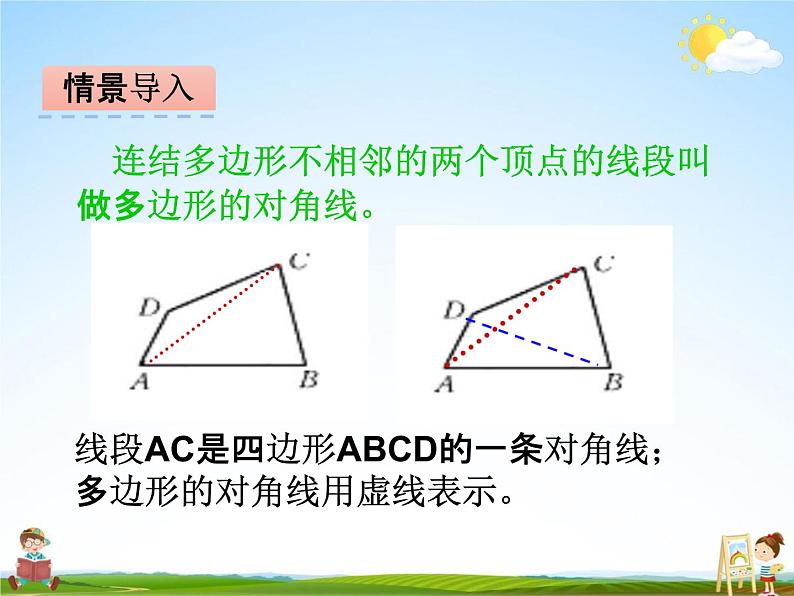
连结多边形不相邻的两个顶点的线段叫 做多边形的对角线。
线段AC是四边形ABCD的一条对角线； 多边形的对角线用虚线表示。
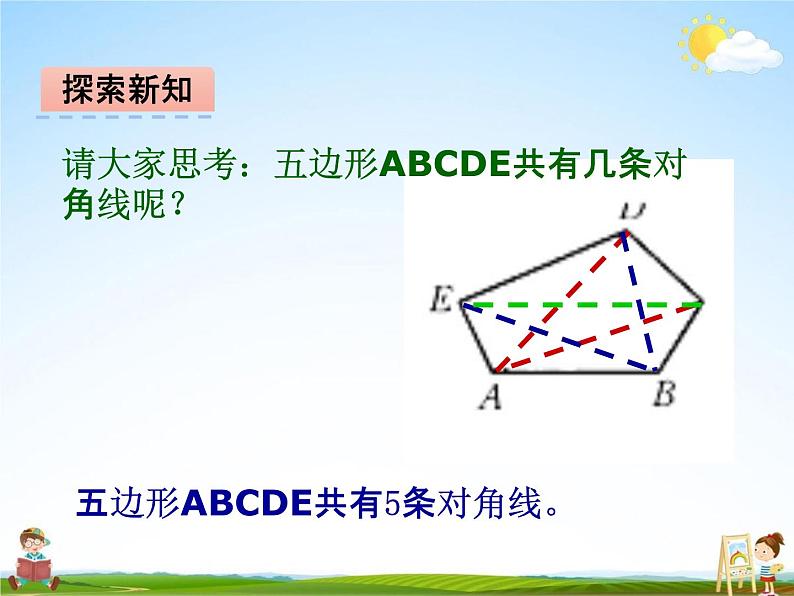
请大家思考：五边形ABCDE共有几条对 角线呢？
五边形ABCDE共有5条对角线。
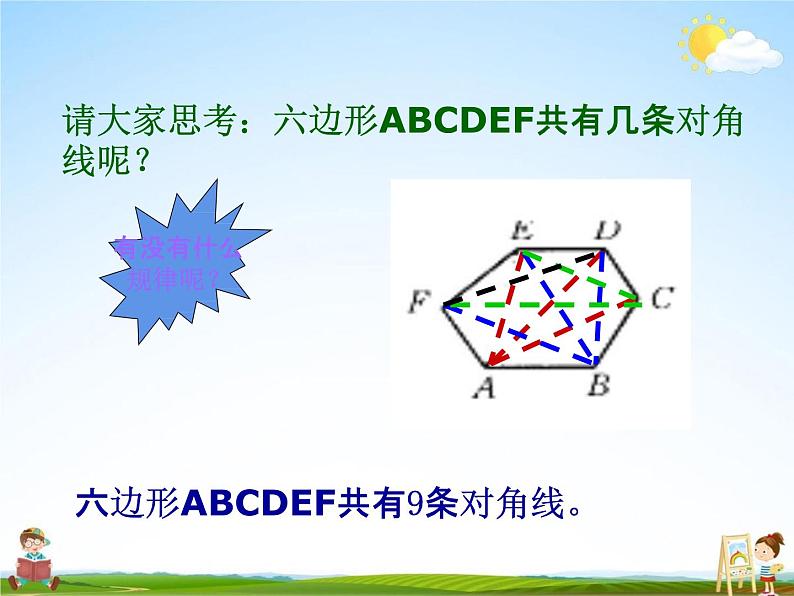
请大家思考：六边形ABCDEF共有几条对角 线呢？
六边形ABCDEF共有9条对角线。
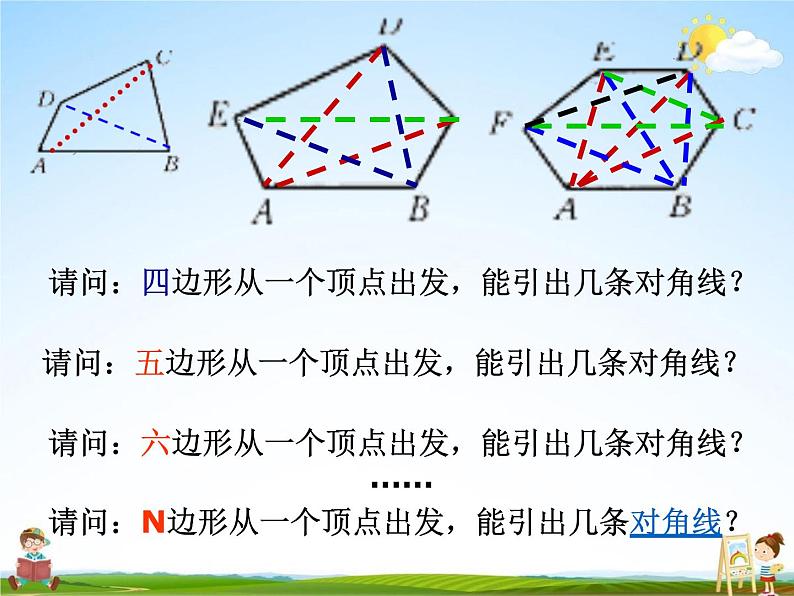
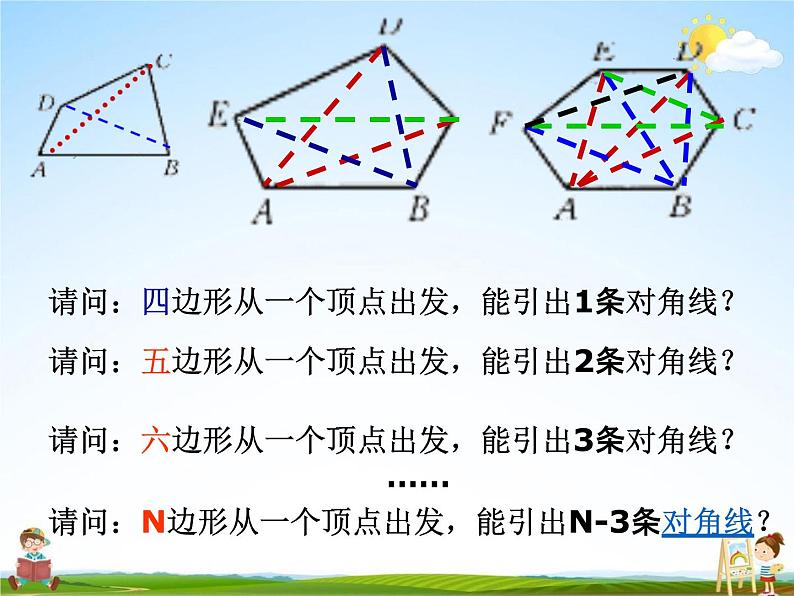
请问：四边形从一个顶点出发，能引出几条对角线？
请问：五边形从一个顶点出发，能引出几条对角线？请问：六边形从一个顶点出发，能引出几条对角线？……请问：N边形从一个顶点出发，能引出几条对角线？
请问：四边形从一个顶点出发，能引出1条对角线？请问：五边形从一个顶点出发，能引出2条对角线？请问：六边形从一个顶点出发，能引出3条对角线？……请问：N边形从一个顶点出发，能引出N-3条对角线？
我们已经知道一个三角形的内角和等于180°， 那么四边形的内角和等于多少呢？五边形、六边形 呢？由此，n边形的内角和等于多少呢？
我们学习数学的 基本思想什么？
那么我们能不能 利用三角形的内角 和，来求出四边形 的内角和，以及五 边形、六边形，n边 形的内角和？
请你认真地想一想，你能通过怎样的方法把多边 形转化为三角形？
180 ° (n-2)
1.从一个顶点出发的对角线有(n-3)条
由此，我们就可以得出 :
n 边形的内角和为_________________．(n-2) 180 °
它有什么作用 呢?知道多边形的边数，可以求出多边形的度 数.知道多边形的度数，可以求出多边形的边数.
求八边形的内角和的度数．
解（ n － 2 ）× 180 °● =（ 8 － 2 ）× 180 °● = 1 080 °
分析: n边形的内角和公式为(n-2) 180 °， 现在知道这个多边形的边数，代入这个公式 既可求出.
已知多边形的内角和的度数为900 °， 则 这个多边形的边数7为_ _______
已知在一个十边形中，九个内角的和 的度数是1290°，求这个十边形的另一 个内角的度数.
解: （ 10 － 2 ）× 180 ° = 1440 °则十边形的另一个内角的度数为1440 °- 1290 ° = 150 °
先求出十边形的内角和再减去1290°,就可 以得出.
那么对于正多边形来说, 又遇到怎样的问题呢?
因为正多边形的每个角相等，所以知道正多边形的边数，就可以求出每一个内角的度数.
（n－2）×180°/ n
正五边形的每一个内角等于_____, 外角等于___.
解:（ n－ 2 ）× 180 ° / n● = （ 5 － 2 ）× 180 ° / 5● = 540 ° / 5● = 108 °
如果一个正多边形的一个内角等于
120°,则这个多边形的边数是解:120°n=（n－2）×180°120°n=n×180°-360 °60°n =360 °n =6
如果一个正多边形的一个内角等于150 °, 则这个多边形的边数A 是_____
A.12B.9C. 8D.7如果一个多边形的每一个外角等于30°,则这 个多边形的边数是 1_2_如果一个多边形的边数增加1,则这个多边形 的内角和 增_加180 °