初中人教版第五章 相交线与平行线综合与测试学案

人教版七年级数学下册《第五章相交线》复习专题训练

专题训练一：利用相交线的性质求角度

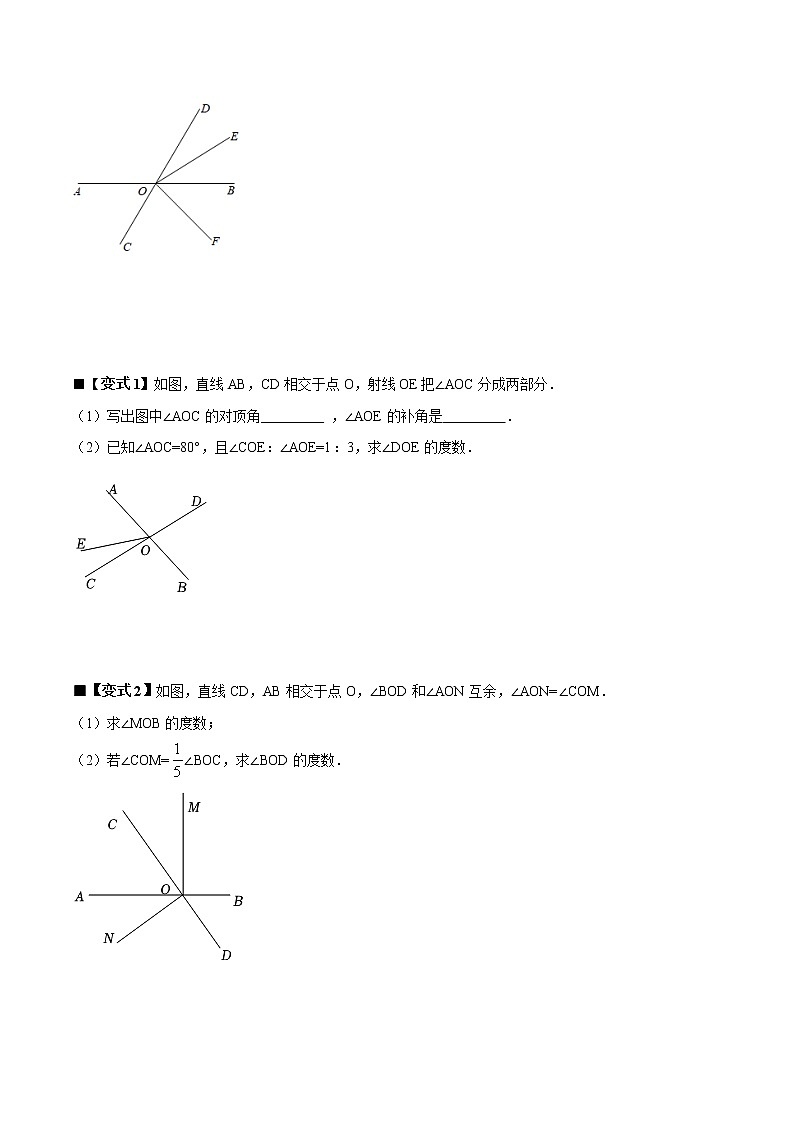
◎【典例一】◎如图,已知直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，若 ∠AOD=100°.

求：(1)∠EOD的度数；      (2)∠AOF的度数.

■【变式1】如图，直线AB，CD相交于点O，射线OE把∠AOC分成两部分．

（1）写出图中∠AOC的对顶角          ，∠AOE的补角是         ．

（2）已知∠AOC=80°，且∠COE：∠AOE=1：3，求∠DOE的度数．

■【变式2】如图，直线CD，AB相交于点O，∠BOD和∠AON互余，∠AON=∠COM．

（1）求∠MOB的度数；

（2）若∠COM=∠BOC，求∠BOD的度数．

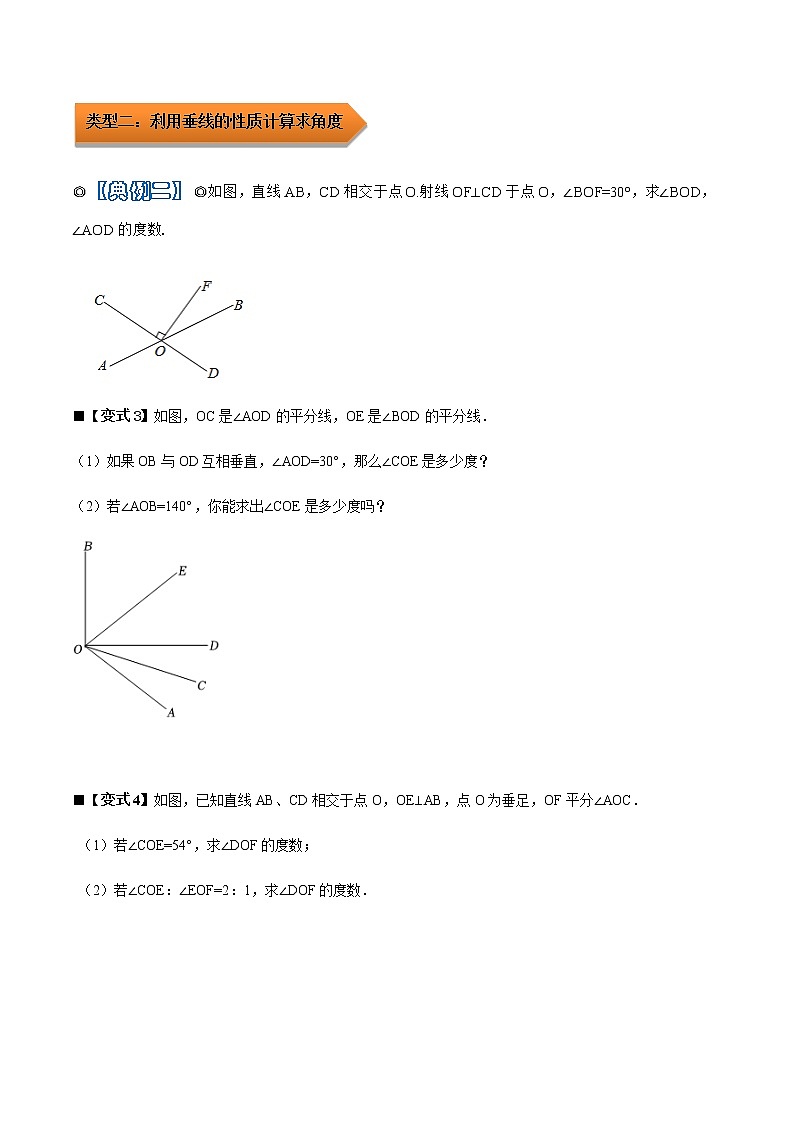
◎【典例二】◎如图，直线AB，CD相交于点O.射线OF⊥CD于点O，∠BOF=30°，求∠BOD，∠AOD的度数.

■【变式3】如图，OC是∠AOD的平分线，OE是∠BOD的平分线．

（1）如果OB与OD互相垂直，∠AOD=30°，那么∠COE是多少度？

（2）若∠AOB=140°，你能求出∠COE是多少度吗？

■【变式4】如图，已知直线AB、CD相交于点O，OE⊥AB，点O为垂足，OF平分∠AOC．

（1）若∠COE=54°，求∠DOF的度数；

（2）若∠COE：∠EOF=2：1，求∠DOF的度数．

◎【典例三】◎如图，直线AB、CD相交于点O，∠AOC=28°，∠BOF=59°，OF平分∠DOE，OE与AB垂直吗？为什么？

■【变式5】如图，直线AB，CD相交于点O，OM⊥AB．

（1）∠AOC的邻补角为∠AOD（写出一个即可）；

（2）若∠1=∠2，判断ON与CD的位置关系，并说明理由；

（3）若∠1=∠BOC，求∠MOD的度数．

■【变式6】如图，点O为直线AB上一点，OE平分∠DOE,OA平分∠COF,若∠AOE=120°，

指出图中互相垂直的直线，并说明理由.

1、（2021秋•瓦房店市期末）如图，已知直线AB与CD相交于点O，OC平分∠AOE，∠AOD=140°．则∠BOE的度数为（      ）

A．120°          B．110°        C．100°             D．80°

2、（2021秋•新昌县期末）如图，点O在直线BD上，已知∠1=20°，OC⊥OA，则∠BOC的度数为（　　）

 A．20°    B．70°       C．80°      D．90°

3、（2021秋•金华期末）如图，三条直线a、b、c相交于一点，则∠1+∠2+∠3=（　　）

A．360°         B．180°       C．120°           D．90°

4、（2021秋•余姚市期末）如图，直线DE与BC相交于点O，∠COE与∠AOE互余，∠BOD=35°，则∠AOE的度数是（ 　　）

A．55°         B．45°       C．35°       D．65°

5、（2021秋•封丘县期末）如图，直线AB，CD相交于点O，EO⊥AB于点O，若∠2=40°，则∠1﹣∠3的度数为（　　）

A．30°      B．25°       C．20°        D．10°

6、（2021秋•无锡期末）如图，直线AB与CD相交于O，OE⊥AB，OF⊥CD，∠AOC=28°24′，则∠COE=     ，图中与∠COE互补的角有             ．

7、（2022•西城区校级开学）已知：如图，三条直线AB，CD，EF相交于O，且CO⊥EF，∠AOE=70°，若OG平分∠BOF，求∠DOG．

8、（2021秋•商河县期末）已知：如图，直线AB、CD相交于点O，∠EOC=90°，OF平分∠AOE．

（1）若∠BOC=40°，求∠AOF的大小．

（2）若∠COF=x°，求∠BOC的大小．

9、（2021秋•覃塘区期末）如图，已知直线AB与CD相交于点O，OE平分∠AOD，∠EOF=90°．对于下列结论：①∠BOC=2∠AOE；②OF平分∠BOD；③∠AOE是∠BOF的余角；④∠AOE是∠COE的补角．其中正确结论的个数是（　　）

A．1               B．2             C．3           D．4

10、（2021秋•瑶海区期末）如图，直线AB，CD交于点O，OE平分∠AOC，OF⊥AB，OG平分∠EOF，若∠BOC=48°，则∠AOG等于         .

11、（2021春•仓山区期中）直线AB，CD相交于点O．OE，OF，OG分别平分∠AOC，∠BOC，∠AOD．下列说法正确的是（　   　）

A．OE，OF在同一直线上          B．OE，OG在同一直线上

B．OG⊥OF                      D．OE⊥OF

12、（2021秋•义乌市期末）如图，已知OB是∠AOC内一条射线，OE平分∠AOC，OF平分∠BOC．

（1）若AO⊥BO，∠BOC=60°，求∠EOF的度数；

（2）试判断∠AOB=2∠EOF是否成立．并请说明理由．

13、（2021秋•石狮市期末）如图，直线AB、CD相交于点O，EO⊥CD，垂足为点O．若∠BOD：∠BOC=1：5．

（1）求∠BOE的大小；

（2）过点O画直线MN⊥AB，若点F是直线MN上一点，且不与点O重合，试求∠EOF的大小．

14、（2020秋•香坊区校级月考）已知∠AOB与∠BOC互为邻补角，OD平分∠BOC，OE⊥OB于点O，若∠AOD=4∠BOC，则∠DOE=          ．

15、（2021秋•鄞州区期末）如图，直线AB，CD相交于点O，OE平分∠BOC．

【基础尝试】

（1）如图1，若∠AOC=40°，求∠DOE的度数；

【画图探究】

（2）作射线OF⊥OC，设∠AOC=x°，请你利用图2画出图形，探究∠AOC与∠EOF之间的关系，结果用含x的代数式表示∠EOF．

【拓展运用】

（3）在第（2）题中，∠EOF可能和∠DOE互补吗？请你作出判断并说明理由．