人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教学设计

这是一份人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教学设计，共8页。教案主要包含了素质教育目标，学法引导，重点·难点·疑点及解决办法，教学过程，课堂总结等内容，欢迎下载使用。
（一）知识教学点
1．掌握平行四边形的判定定理1、2、3、4，并能与性质定理、定义综合应用．
2．使学生理解判定定理与性质定理的区别与联系．
3．会根据简单的条件画出平行四边形，并说明画图的依据是哪几个定理．
（二）能力训练点
1．通过“探索式试明法”开拓学生思路，发展学生思维能力．
2．通过教学，使学生逐步学会分别从题设或结论出发寻求论证思路的分析方法，进一步提高学生分析问题，解决问题的能力．
（三）德育渗透点
通过一题多解激发学生的学习兴趣．
（四）美育渗透点
通过学习，体会几何证明的方法美．
二、学法引导
构造逆命题，分析探索证明，启发讲解．
三、重点·难点·疑点及解决办法
1．教学重点：平行四边形的判定定理1、2、3的应用．
2．教学难点：综合应用判定定理和性质定理．
3．疑点及解决办法：在综合应用判定定理及性质定理时，在什么条件下用判定定理，在什么条件下用性质定理（强调在求证平行四边形时用判定定理，在已知平行四边形时用性质定理）
四、教学过程
（一）复习平形四边的定义（强调定义即是性质又是判定）和性质
平行四边形的定义：两组对边分别平行的四边形叫做平行四边形．
平行四边形的性质：对边相等，对角相等，对角线互相平分．
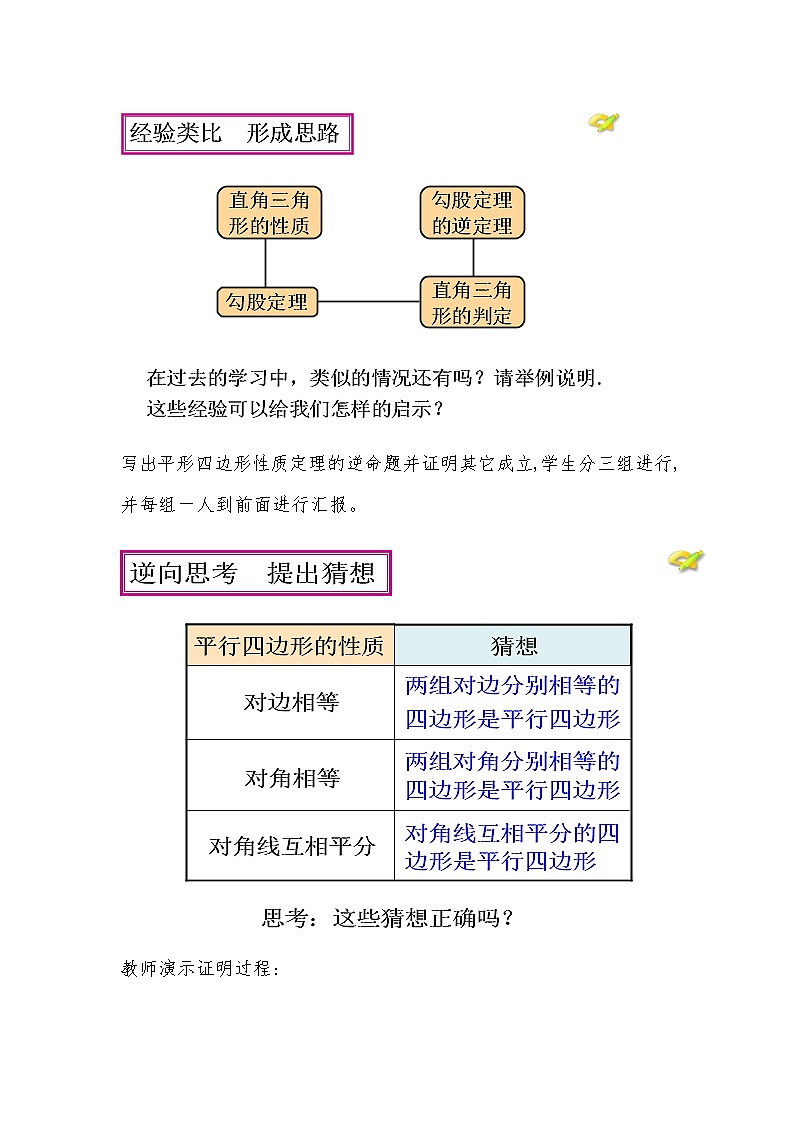
（二）通过对平形四边形的性质分析并类比勾股定理等得出平形四边形的性质与判定的关系
写出平形四边形性质定理的逆命题并证明其它成立，学生分三组进行，并每组一人到前面进行汇报。
教师演示证明过程：
（三）小结所学内容
现在，我们一共有哪些判定平行四边形的方法呢？
定义：两组对边分别平行的四边形叫做平行四边形．
判定定理：
（1）两组对边分别相等的四边形是平行四边形；
（2）两组对角分别相等的四边形是平行四边形；
（3）对角线互相平分的四边形是平行四边形．
（四）、练习
1、四边形ABCD中，若∠A＋∠B＝180°，∠C＋∠D＝180°，则这个四边形______(填“是”、“不是”或“不一定是”)平行四边形．
2、四边形ABCD中，若∠A＝∠B，∠C＝∠D，则这个四边形_____(填“是”、“不是”或“不一定是”)平行四边形．
3、四边形ABCD中，AC、BD为对角线，AC、BD相交于点O，BO＝4，CO＝6，当AO＝_____，DO＝______时，这个四边形是平行四边形．
4、在四边形ABCD中，AB=CD,BC=AD,四边形ABCD____(填“是”、“不是”或“不一定是”)平行四边形．
5 巩固知识
6、综合运用
7、拓展学习
五、课堂总结
总结：平形四边形的判定方法
（1）定义：两组对边分别平行的四边形是平行四边形
（2）两组对边分别相等的四边形是平行四边形；
（3）两组对角分别相等的四边形是平行四边形；
（4）对角线互相平分的四边形是平行四边形．