数学必修 第一册2.1 等式性质与不等式性质教课ppt课件

这是一份数学必修 第一册2.1 等式性质与不等式性质教课ppt课件，共40页。PPT课件主要包含了讲解范例，探究1，探究2，形的角度，数的角度，典型例题，课后练习等内容，欢迎下载使用。

同学们，为什么教材要把等式性质与不等式性质放在一起来学习？
18世纪的法国有一个农民家庭出身的数学家和天文学家——拉普拉斯(Pierre—Simn de laplace1749—1827)。拉普拉斯是现代概率论的奠基者之一。学物理的人对他很熟。 　　他有一个很好的品德，就是对于年青一代的数学家当作自己的孩子，帮助他们和鼓励他们。有一些人的发现事实上是他早在几十年前就得到了，但他也是把这发现的荣誉让给年青人而不是自己占有、不像一些所谓“专家”对这些新生的力量，在妒忌之余，加以阻挠打击。 　　拉普拉斯在关于概率论的哲学问题的一篇文章里曾经指出：“在数学这门科学里，我们发现真理的主要工具是归纳和类比(inductin and analgy)。”这里他指出了发现数学定理的一个方法。
1、为什么要学习等式性质与不等式性质？
在现实世界和日常生活中，大量存在着相等关系和不等关系。例如多与少、大于与小、长与短、高与矮、远与近、快与慢、长与跌、轻与重、不超过或不等于。类似于这样的问题，反映在数量上，就是相等与不等。相等用等式表示，不等用不等式表示。 说句不严格的话，相等关系少，不等关系多，相等关系是相对的，不等关系是绝对的。现实中大部分是不等关系，少部分是相等关系。这种相对与绝对的例子很多。比如：静止是相对的，运动是绝对的 下面我们看几个模型，同学们自己抽象出不等关系。
你能用不等式与不等式组表示下列问题中的不等关系吗？ （1）某路段限速40km/h; （2）某品牌酸奶的质量检查规定，酸奶中脂肪的含量f应不少于2.5%，蛋白质的含量p应不少于2.3%; （3）三角形两边之和大于第三边、两边之差小于第三边； （4）连接直线外一点与直线上各点的所有线段中，垂线最短。
问题2：某种杂志原以每本2.5元的价格销售，可以售出8万本.根据市场调查，若单价每提高0.1元，销售量就可能相应减少2000本.若把提价后杂志的定价设为x元，怎样用不等式表示销售的总收入仍不低于20万元？
这是道初中难题跟高中毫无关系。到高中变基础题。有的同学高中数学学不下去，是因为这里有个台阶上不去，在初中只会做容易题和中档题。
除了以上列举的现实生活中的不等关系，你还能列举出你周围日常生活中的不等关系吗？
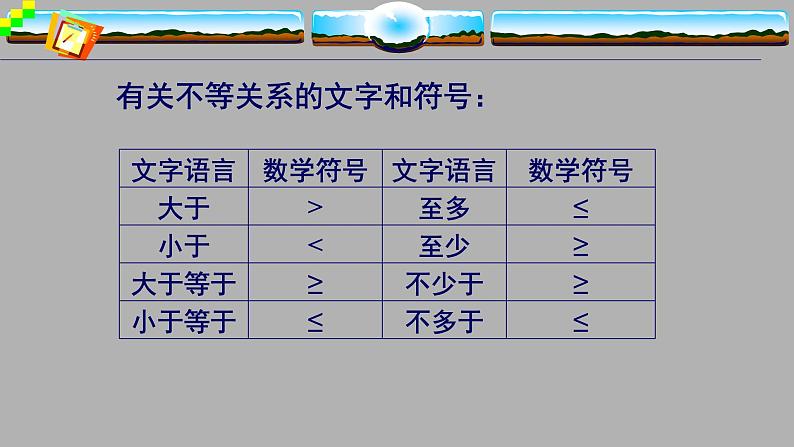
有关不等关系的文字和符号：
在初中，我们知道了一些不等式的基本事实：
这个事实是从现实世界中人们根据生产生活中的经验归纳出来的。它不能被证明，相当于是个公理，与公理的情况类似。
这个事实有个应用，即我们要比较两个实数的大小，可以转化为比较它们的差与0的大小。
例3. 比较(a＋3)(a－5)与(a＋2)(a－4)的大小.
虽然a未知但做差a抵消掉。
例4. 已知x≠0，比较(x2＋1)2与x4＋x2＋1的大小.
虽然x未知，但做差结果是x2。
作差比较法的步骤是：1. 作差；2. 变形：配方、因式分解、通分、分母 （分子）有理化等；3. 判断符号；4. 作出结论．
反思：1、一题多解：做差、做商。做差是与0比较，做商是与1比较。2、一杯含a克糖的糖水共b克再加m克糖，糖水变甜。
2002年在北京举行的第24届国际数学家大会会标
思考：这会标中含有怎样的几何图形？
思考：你能否在这个图案中找出一些相等关系或不等关系？
问1：在正方形ABCD中,设AF=a,BF=b,则正方形的面积为S=
图片说明：当直角三角形变为等腰直角三角形，即a=b时，正方形EFGH缩为一个点，这时有
当a=b时 a2+b2－2ab =(a－b)2=0
数学知识有两个角度的本质，形的角度本质和数的角度本质即代数角度本质的和几何角度本质。
我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．
结论：一般地，对于任意实数a、b，我们有
此不等式称为重要不等式
当且仅当a=b时，等号成立
1、学习数学有什么用？
荷兰数学家弗赖登塔尔的，他说：“与其说是学习数学，还不如说是学习‘数学化’；与其说是学习公理系统，还不如说是学习‘公理化’；与其说是学习形式体系，还不如说是学习‘形式化’。”
数学教育家米山国藏指出：“学生进入社会后，几乎没有机会应用它们在初中或高中所学到的数学知识，因而这种作为知识的数学，通常在学生出校门后不到一两年就忘掉了，然而不管从事什么业务工作，那种铭刻于头脑中的数学精神和数学思想方法，却长期地在他们的生活和工作中发挥着重要作用。”
所以学习数学，数学忘记了，但数学化不会忘记，学习公理，公理忘记了，但公理化不会忘记，学习形式体系，形式体系忘记了，但形式化不会忘记。也就是数学化、公理化、形式化一辈子都对你产生影响。
中国人的思维缺陷
1、不证而论 比如不懂逻辑学上的“充足理由律”，给出论点来往往不证而论，只有论点，没有论据。
2、以“经典、经验、想当然”作为论据
参考文章：《中国人思维的五大缺陷》作者：芦笛
总结：中国数学是经验型的，结构松散毫无逻辑，中国人做事也不讲逻辑。
西方人思维优点
擅长逻辑，比如平面几何的公理系统，从几个公理出发当成起点推出定理、性质、推论。或由以定理、性质、推论为依据推出定理、性质、推论，每一步都有论据，这论据要么是公理要么是定理、性质、推论。最后形成严密的公理化系统，注意是严密。逻辑学就是发达于西方. 学习数学有点就是学习西方人如何思维,高考大部分考西方的思维方式。只有算法是考中国人思维方式
同学们会梳理等式的基本性质吗，再观察它们的共性，你能归纳一下发现等式基本性质的方法吗？
可以发现，性质1，性质2反映了相等关系自身的特性，性质3,4,5是从运算的角度提出，反映了等式在运算变化中的不变性。
类比等式的基本性质，你能猜想不等式的基本性质，并加以证明吗？
这个事实是从现实世界中人们根据生产生活中的经验归纳出来的。它不能被证明，相当于是个公理，与公理的情况类似。它是不等式证明的起点。
性质1：如果a>b，那么bb。即
性质2如果a>b,b>c，那么a>c.即
初中我们学习不等式是1、零碎 2、杂乱 3、感性认识 4、不系统 5、无意识的。无意识是什么意思？我们初中解不等式性质1到性质8都已经变成了自动化操作，自己都没有意识到。
而高中需要什么提高就是：1、公理化 2、系统化 3、理性认识 4、有意识的。注：公理化相当于公理是“道”或受精卵。“道”生一，一生二，二生三，三生万物，相当于受精卵慢慢发育成人体。
把性质1到性质8当成公理，其他是推导出来
证明性质1到性质8的论据除了实数a,b大小的比较有以下事实外，还有些事实。1、正数大于0，也大于一切负数；负数小于0，也小于一切正数；2、正数的相反数是负数，负数的相反数是正数。3、正数相加是正数，负数相加是负数。4、正正得正，负负得正，正负得负。5、正数的倒数是正数，负数的倒数是负数。二、这节课可以实践我的完美教室理论。每个学生（中国人）认识自己，然后是发现自己中国人即思维有缺陷，然后是突破自己，成为那个像西方人思维的自己，自动化后做这个最好的自己。
分析：分a,b异号和同号。异号易知大小。
如果不是证明题可以根据经验解题比如特殊法，如果是证明题要每一步有论据。
例3 若a＜b＜0，判断下列结论是否成立.
1.如果30＜x＜42， 16＜y＜42 ，求x+y，x-2y， 的范围.
注：大部分经验是正确的，少部分经验是错误的。同学想当然的解法是把两不等式相减或相除，这经验是错误的。