人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式教学演示课件ppt

这是一份人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式教学演示课件ppt，共20页。PPT课件主要包含了2基本不等式，探究2，探究3等内容，欢迎下载使用。
为什么称为基本不等式？ 主要是因为它可以作为不等论的基本定理，成为支撑其他处所非常重要结果的基石，同时它也是解决许多最值问题的有力工具。
温州市瓯海区三溪中学 张明
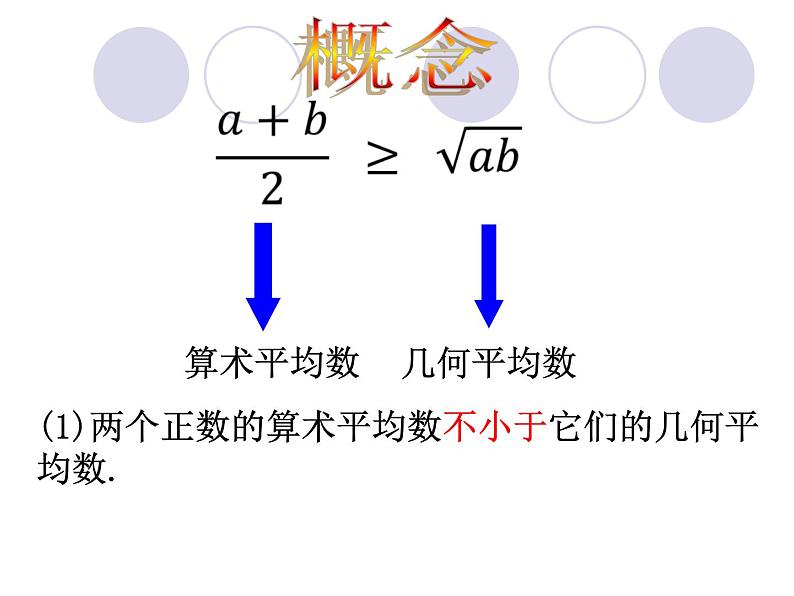
(1)两个正数的算术平均数不小于它们的几何平 均数.
同学们，基本不等式中a>0,b>0需要死记硬背吗？
答：a、b一正一负，不等式右边根号里无意义。如果a、b两负，不等式左边0，不等式显然不成立。如果a、b=0在实际中用处不大，所以研究这样的不等式没有多少价值。
基本不等式还有其他证法吗？孙维刚老师说：“解题要一题多解，一题多变，多解归一等”
上节课我们用公理化思想梳理了不等式的一些性质，那好能不能用这些性质来证明一些不等式定理呢？这也是公理化思想的一种表达形式。
从问题的结论出发，追溯导致结论成立的条件，逐步上溯，直到使结论成立的条件和已知条件吻合为止。
分析法（逆推证法或执果索因法）
一般地，从要证明的结论出发，逐步寻求推证过程中，使每一步结论成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种证明的方法叫做分析法。其特点是：执果索因，即要证结果Q，只需证条件P.
分析法像警察破案，一步步推理，最终找到犯罪的证据。整个案件清晰明朗。
对基本不等式的几何意义作进一步探究:
如图,AB是圆的直径，Q是AB上任一点，AQ=a,BQ=b,过点Q作垂直于AB的弦PQ，连AP,BP,则PQ=____,半径AO=_____
几何意义：圆的半径不小于圆内半弦长
数学知识有两个角度本质，形的角度本质和数的角度本质即代数角度本质和几何角度本质。
代数角度本质是一是重要不等式的推论二是完全平方数大于等于0，几何角度本质是半径不小于半弦。
若有，那么当 x=y 时，最小值为：
若有，那么当 x=y 时，最大值为
例1：（1）用篱笆围成一个面积为100m的矩形菜园，问这个矩形的长、宽各为多少时，所用篱笆最短。最短的篱笆是多少？
解：设矩形菜园的长为x m，宽为y m，
则xy=100，篱笆的长为2（x+y）m.
等号当且仅当x=y时成立，此时x=y=10.
因此，这个矩形的长、宽都为10m时，所用的篱笆最短，最短的篱笆是40m.
强调：两个正变量积为定值，则和有最小值，当且仅当两值相等时取最值。
（2）用一段长为36m的篱笆围成一个矩形菜园，问这个矩形菜园的长和宽各为多少时，菜园的面积最大，最大面积是多少？
则 2（ x + y ）= 36 , x + y = 18
矩形菜园的面积为xym2
当且仅当x=y,即x=y=9时，等号成立
因此，这个矩形的长、宽都为9m时，菜园面积最大，最大面积是81m2
强调：两个正变量和为定值，则积有最大值，当且仅当两值相等时取最值。
反思：1、当两数是正数时，为什么积定值，和有最小值不是最大值？2、为什么和是定值，积有最大值不是最小值？
答:1、当两正数积是定值，则两正数不能一起无限小，所以和必有最小值，但可以一个无限小一个无限大，所以和没有最大值。2、当两正数和是定值，则两正数不能一起无限小也不能一起无限大，但其中一个正数可以无限小，另一正数接近定值，所以积有最大值没有最小值。
那好，理论能反映现实吗？这有没有现实依据？
我们想用篱笆围成一个面积是定值的矩形，为了省钱，希望篱笆用的越短越好。我们想要用一定长度的篱笆围成一个矩形，希望矩形的面积越大越好，因为面积越大，我们使用的空间就越大。相当于花最少的钱赚取最大的利益。这是人的本性。在经济学上都是假定人是自私自利的，即人是坏的。西方政治制度的建立也是假定人是坏的。
应用基本不等式求最值的条件：
若等号成立，a与b必须能够相等
强调：求最值时要考虑不等式是否能取到“＝”
例2:某工厂要建造一个长方体形无盖贮水池,其容积为4800m3,深为3m.如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?
分析:水池呈长方体形,它的高是3m,底面的长与宽没有确定.如果底面的长与宽确定了,水池的总造价也就确定了.因此应当考察底面的长与宽取什么值时水池总造价最低。