高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合优秀教学ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合优秀教学ppt课件，文件包含新教材622排列数pptx、新教材622排列数教学设计docx等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

问题：前面我们计算了几个简单的排列问题，那么，对于一般的排列问题要如何计算所有的排列的个数呢？应该如何表示呢？
复习回顾：排列的概念：
一般地，从n个不同的元素中取出m（m≤n）个元素，并按照一定的顺序排成一列，叫做从n个不同的元素中取出m个元素的一个排列。
知识点1：排列数的概念
一般地，我们把从n个不同的元素中取出m（m≤n）个元素的所有不同排列的个数，叫做从n个不同的元素中取出m个元素的排列数。
问题2：从4个不同的元素中取处3个元素排成一列，应该如何表示?
问题1：从3个不同的元素中取处2个元素排成一列，应该如何表示?
问题3：从n个不同的元素中取出2个元素的排列数如何表示？计算结果又是什么呢？
第2步，填第2个位置的元素，可以从剩下的(n-1)个元素中任选1个，有(n-1)种选法。
根据分步乘法计数原理，2个空位的填法种数为：
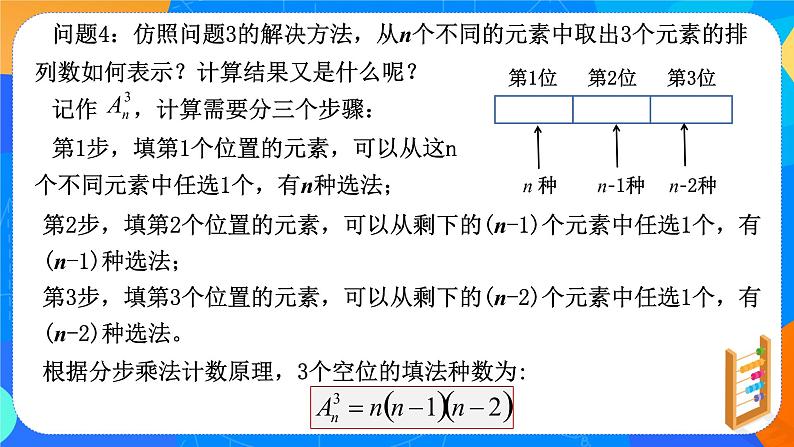
问题4：仿照问题3的解决方法，从n个不同的元素中取出3个元素的排列数如何表示？计算结果又是什么呢？
第2步，填第2个位置的元素，可以从剩下的(n-1)个元素中任选1个，有(n-1)种选法；第3步，填第3个位置的元素，可以从剩下的(n-2)个元素中任选1个，有(n-2)种选法。根据分步乘法计数原理，3个空位的填法种数为:
假定有排好顺序的m个空位如图，从n个不同元素中取出m个元素去填空，一个空位填上一个元素，每一种填法就对应一个排列。因此，所有不同填法的种数就是排列数。
填空可以分为m个步骤完成：第1步，从n个不同元素中任选1个填在第1位，有n种选法；第2步，从剩下的(n-1)个元素中任选1个填在第2位，有(n-1)种选法；第3步，从剩下的(n-2)个元素中任选1个填在第3位，有(n-2)种选法；……第m步，从剩下的(n-m+1)个元素中任选1个填在第m位，有(n-m+1)种选法.根据分步乘法计数原理，m个空位的填法种数为：
知识点2：排列数公式(一)
这里，m,n∈N*，并且m≤n，这个公式叫做排列数公式。
(1)后面每一个因数比前一个因数少1；
知识点3：全排列的概念(阶乘)
特别地，我们把n个不同的元素全部取出的一个排列，叫做n个元素的一个全排列。
这时，排列数公式中的m=n，即有：
即将n个不同的元素全部取出的排列数，等于正整数1到n的连乘积。
正整数1到n的连乘积，叫做n的阶乘，用n！表示。
于是，n个元素的全排列数公式可以写成：
另外，我们规定 0！=1。
知识点4：排列数公式(二)
因此，排列数公式也可以写成：
例4 用0~9这10个数字，可以组成多少个没有重复数字的三位数？
分析：在0~9这10个数字中，因为0不能在百位上，而其他9个数字可以在任意数位上，因此0是一个特殊的元素。一般地，我们可以从特殊元素的位置入手来考虑问题。
根据分步乘法计数原理，所求的三位数的个数为: