数学七年级下册第9章 从面积到乘法公式综合与测试教课ppt课件

这是一份数学七年级下册第9章 从面积到乘法公式综合与测试教课ppt课件，共23页。PPT课件主要包含了因式分解，练一练，pa+pb+pc，整体思想，公式的变形与运用等内容，欢迎下载使用。
1.单项式乘以单项式：
把它们的系数、同底数的幂分别相乘，对于只在一个单项式里出现的字母连同它的指数作为积的一个因式。
2.单项式乘以多项式：
m(a+b+c)=ma+mb+mc
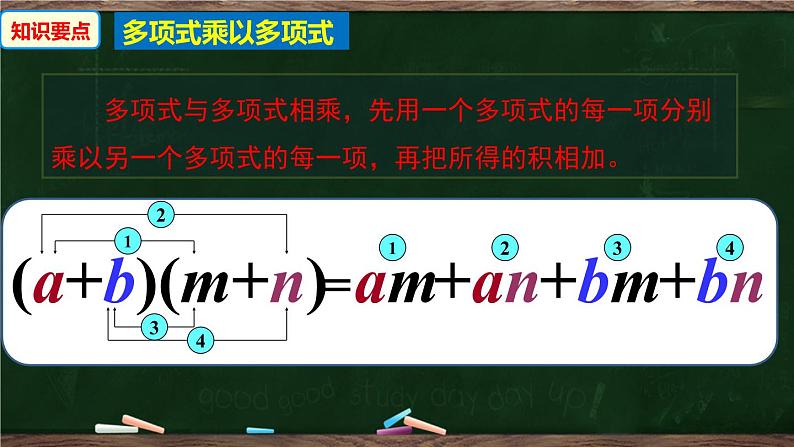
3.多项式乘以多项式：
(a+b)(m+n)=a(m+n)+b(m+n)=am+an+bm+bn
(x±y)2=x2±2xy+y2
(x+y) (x-y)=x2-y2
单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.
单项式与单项式的乘法法则
（1）先系数相乘，注意符号运算；（2）相同字母或相同因式的幂相乘（即同底数幂相乘）；（3）其余字母连同它的指数不变，作为积的因式.
单项式乘以多项式的法则
（1）依据是乘法分配律（2）积的项数与多项式的项数相同.
单项式与多项式相乘，就是用单项式乘多项式的每一项，再把所得的积相加.
a(b+c+d)=ab+ac+ad
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加。
(a+b)2=a2+2ab+b2； (a-b)2=a2-2ab+b2
速记口诀： 首平方，尾平方， 乘积2倍放中央， 符号确定看前方.
两数和(或差)的平方，等于这两数的平方和，加上(或减去)这两数乘积的2倍.
（1）结果为三项式；（2）结果中有两项是两数的平方和；（3）结果中的另一项是两数积的2倍，且与左边中间的符号相同;（4）公式中的字母a，b可以表示数，单项式和多项式等代数式.
例1 运用完全平方公式计算：
(a +b)2 = a2 + 2 ab + b2
解: (4m+n)2 =
= 16m2+8mn +n2
(4m)2+2•(4m) •n+n2
判断下列各式的计算是否正确，
(a+b) (a-b) =a2-b2
两数和与这两数差的积,等于这两数的平方差.
（1）(a+b) (-a-b) （4）(a-b) (a+b)（2）(a+b) (-a+b) （5）(a-b) (-a-b)（3）(a-b) (a+b) （6）(a-b) (-a+b)
例2：运用平方差公式计算：
(1)（3x+2)(3x-2) (2) (-x+3y)(x+3y)
解：(1) （3x+2)(3x-2)
(a+ b) (a- b) = a2 - b2
(2) (-x+3y)(x+3y)
=(3y-x)(3y+x)
（1）结果一定是积的形式；（2）每个因式必须是整式；（3）各因式要分解到不能再分解为止．
把一个多项式化成几个整式的积的形式叫做因式分解．
2.下列式子从左到右哪个是因式分解,哪个整式乘法？它们有什么关系？
(1). a(x+y)=ax+ay (2). ax+ay=a(x+y)
1.下列变形是否是因式分解？(1) 3x2y-xy+y=y(3x2-x)；(2) x2-2x+3=(x-1)2+2；(3) x2y2+2xy-1=(xy+1)(xy-1)；(4) xn(x2-x+1)=xn+2-xn+1+xn.
例3 找 3x 2 – 6 xy 的公因式.
多项式中各项都含有的相同因式，叫做这个多项式的公因式.
这个多项式有什么特点？
因式分解方法：1、提公因式法
确定公因式的方法为三定：定系数；定字母；定指数
字母：各项中相同的字母
指数：相同字母的最低次幂
(2)完全平方公式：a2±2ab+b2=(a±b)2
(1)平方差公式：a2-b2=(a+b)(a-b).
因式分解方法：2、运用公式法
a2和b2的符号如何时可以用平方差公式？
（ ）（ ）（ ）（ ）
a2 - b2 =
=[(x＋p)＋(x＋q)] [(x＋p)－(x＋q)]
=(2x+p+q)(p-q)
完全平方式的特点： 1. 必须是三项式（或可以看成三项的）； 2.有两个同号的数或式的平方（两数的平方和）； 3.中间有两底数之积的±2倍.
简记口诀：首平方，尾平方，首尾2倍在中央.
凡具备这些特点的三项式，就是完全平方式，将它写成完全平方形式，便实现了因式分解.
下列各式是不是完全平方式？ （1）a2－4a+4; （2）1+4a²; （3）4b2+4b-1; （4）a2+ab+b2; （5）x2+x+0.25.
例5 分解因式：（1）16x2+24x+9；（2）-x2+4xy-4y2.
分析：在（1）中， 16x2=(4x)2， 9=3²，24x=2·4x·3， 所以16x2+24x+9是一个完全平方式， 即16x2 + 24x +9= (4x)2+ 2·4x·3 + (3)2
解： (1)16x2+ 24x +9 = (4x)2 + 2·4x·3 + (3)2
(2)-x2+ 4xy-4y2 =
=- (x -2y)2.
= (4x + 3)2；
-(x2-4xy+4y2)
因式分解与整式乘法关系
2、已知：x2+5y2+4xy-6y+9=0，求xy的值.
1、已知：4x2+9y2+4x-6y+2=0，求x、y的值.
1、(a+b)2=(a-b)2+4ab
2、(a-b)2=(a+b)2-4ab
3、a2+b2=(a+b)2-2ab
4、a2+b2=(a-b)2+2ab