初中数学苏科版八年级下册10.2 分式的基本性质教案及反思

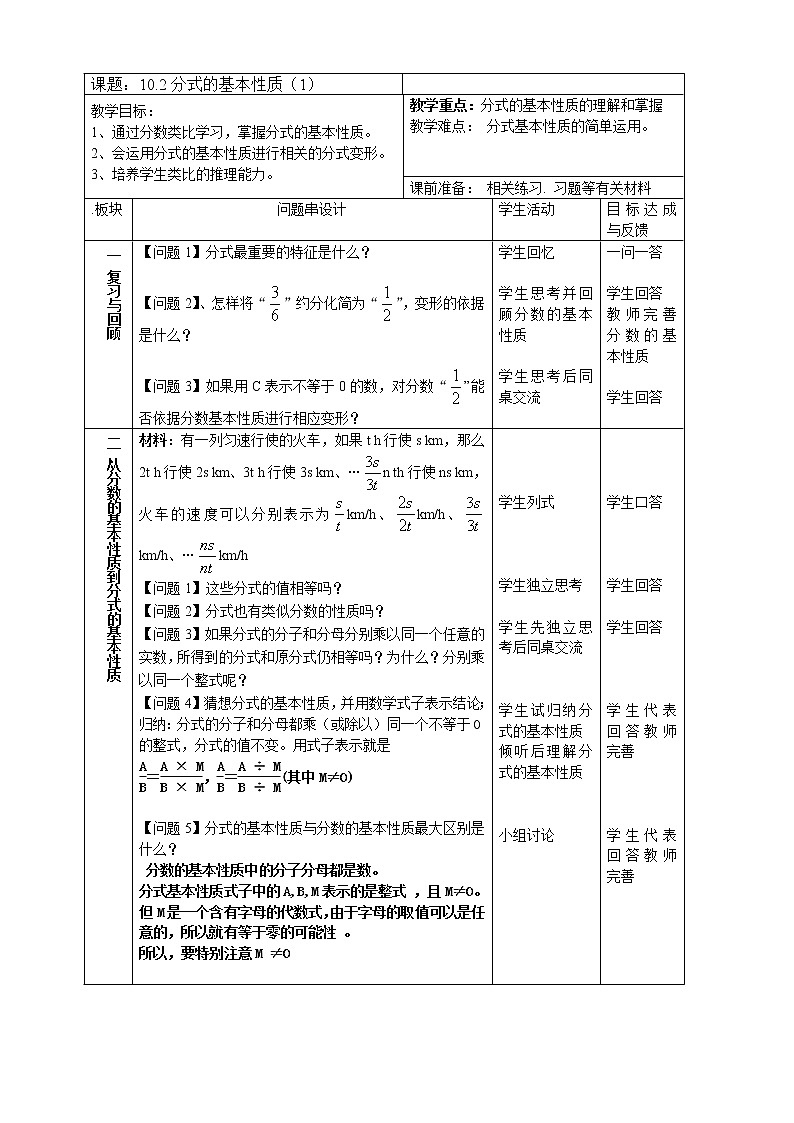
这是一份初中数学苏科版八年级下册10.2 分式的基本性质教案及反思，共2页。
教学目标：
1、通过分数类比学习，掌握分式的基本性质。
2、会运用分式的基本性质进行相关的分式变形。
3、培养学生类比的推理能力。
教学重点：分式的基本性质的理解和掌握
教学难点： 分式基本性质的简单运用。
课前准备： 相关练习. 习题等有关材料
.板块
问题串设计
学生活动
目标达成与反馈
一．复习与回顾
【问题1】分式最重要的特征是什么？
【问题2】、怎样将“”约分化简为“”，变形的依据是什么？
【问题3】如果用C表示不等于0的数，对分数“”能否依据分数基本性质进行相应变形？
学生回忆
学生思考并回顾分数的基本性质
学生思考后同桌交流
一问一答
学生回答
教师完善分数的基本性质
学生回答
二、从分数的基本性质到分式的基本性质
材料：有一列匀速行使的火车，如果t h行使s km，那么2t h行使2s km、3t h行使3s km、…n th行使ns km，火车的速度可以分别表示为km/h、km/h、km/h、…km/h
【问题1】这些分式的值相等吗？
【问题2】分式也有类似分数的性质吗？
【问题3】如果分式的分子和分母分别乘以同一个任意的实数，所得到的分式和原分式仍相等吗？为什么？分别乘以同一个整式呢？
【问题4】猜想分式的基本性质，并用数学式子表示结论；
归纳：分式的分子和分母都乘（或除以）同一个不等于0的整式，分式的值不变。用式子表示就是
eq \f(A,B) ＝ eq \f(A×M,B×M) ， eq \f(A,B) ＝ eq \f(A÷M,B÷M) (其中M≠0)
【问题5】分式的基本性质与分数的基本性质最大区别是什么？
分数的基本性质中的分子分母都是数。
分式基本性质式子中的A,B,M表示的是整式 ，且M≠0。但M是一个含有字母的代数式，由于字母的取值可以是任意的，所以就有等于零的可能性 。
所以，要特别注意M ≠0
学生列式
学生独立思考
学生先独立思考后同桌交流
学生试归纳分式的基本性质
倾听后理解分式的基本性质
小组讨论
学生口答
学生回答
学生回答
学生代表回答教师完善
学生代表回答教师完善
三、分式基本性质的应用与巩固
【问题1】填空：
(1) eq \f(a,b) ＝ eq \f(ab,( )) ； (2) eq \f( eq \f(1,2) a2+b2,(a+b)) ＝ eq \f(( ),2a+2b) ；(3) eq \f(3a,a+6) ＝ eq \f(6ab,( )) (b≠0)；(4)3x－2＝ eq \f(( ),3x+2) (x≠－ eq \f(2,3) )；(5) eq \f(( ),x2-4y2) ＝ eq \f(x,x+2y) ； (6) eq \f(6a2-2ab,( )) ＝3a-b.
【问题2】不改变分式的值，把下列各式的分子、分母中的各项的系数化为整数。
（1） eq \f(0.5x+y,0.2x-4) (2) eq \f( eq \f(1,3) m-0.5,1-0.25m)
【问题3】不改变分式的值，使下列分式的分子和分母都不含“-”号

【问题4】不改变分式的值，使下列分式的分子与分母的最高次项的系数是正数：

【问题5】根据刚才所学完成下列练习：
1、课本练习题第1、2题
2、将 eq \f(a2+5ab,3a-2b) 中的a、b都扩大4倍，则分式的值（ ）
A.不变 B.扩大4倍 C.扩大8倍D. 扩大16倍
3、使等式 eq \f(7,x+2) ＝ eq \f(7x,x2+2x) 自左到右变形成立的条件是 （ ）
A．x0 C.x≠0 D.x≠0且x≠7
4、《随》24页第7题。
学生先独立思考后在练习本上写出答案
学生独立思考后同桌交流
学生独立思考后同桌交流
学生独立思考后同桌交流
学生独立完成
同桌互帮互纠
学生思考
学生先独立思考后同桌交流
学生先独立思考后小组讨论
一问一答
学生回答
教师板书
学生回答
教师板书
学生回答
教师板书
教师巡视
个别指导
学生回答
一问一答
学生代笔回答
小结
本课我们学习了分式的基本性质，是什么？
学生回忆
师生共同归纳