九年级下册5.5 用二次函数解决问题教案及反思

这是一份九年级下册5.5 用二次函数解决问题教案及反思，共3页。
教学内容
5.5 用二次函数解决问题（1）
教学目标
知识与技能：能根据实际问题中变量之间的关系，确定二次函数的表达式。
过程与方法：能用二次函数的有关知识解决问题。通过用二次函数表述数量变化及其关系的过程，体会二次函数是刻画现实世界数量关系的有效数学模型。
情感态度与价值观：在解决问题的过程中，感悟数学具有抽象、严谨和应用广泛的特点，体会数学的价值。
教学重点
利用二次函数解决实际问题
教学难点
最值问题的考虑
教具学具
PPT 多媒体
教学过程
教师活动
学生活动
设计意图
一、
问题导入
铺垫课题
问题一：
用 16 m 长的篱笆围成矩形的养兔场，怎样围可使小兔的活动范围最大？
这个问题的结论我们已经知道了，那么如何利用已经学过的知识，严谨地说明这一点呢？
设矩形的一边长为x米，则另一边为（8-x）米
矩形的面积
当x=4时，
答：当围成变成为4米的正方形时，面积最大。
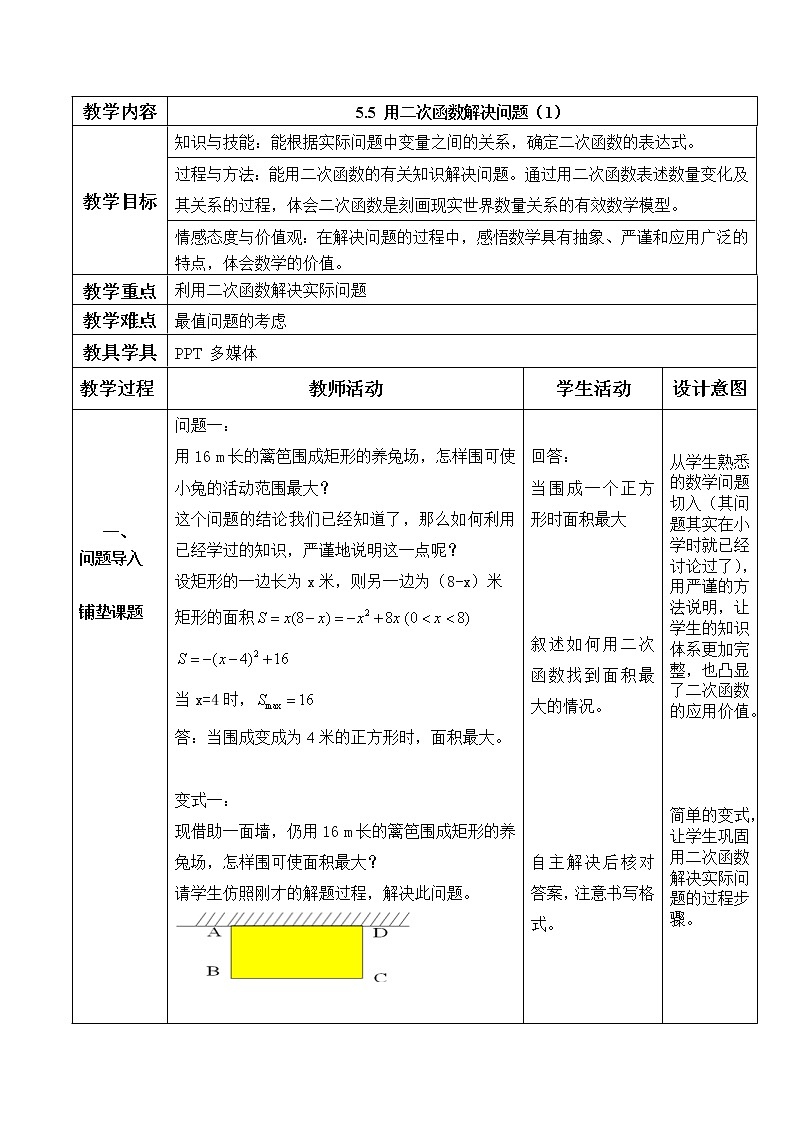
变式一：
现借助一面墙，仍用 16 m 长的篱笆围成矩形的养兔场，怎样围可使面积最大？
请学生仿照刚才的解题过程，解决此问题。
变式二：
若可借用的墙长度为6m ，仍用 16 m 长的篱笆围成矩形的养兔场，怎样围可使面积最大？
分析：变式二与变式一相比，改变的是什么？
解：设米，则 米
当时，
总结：实际问题注意自变量取值范围
回答：
当围成一个正方形时面积最大
叙述如何用二次函数找到面积最大的情况。
自主解决后核对答案，注意书写格式。
回答：
自变量的取值范围
此问题中
从学生熟悉的数学问题切入（其问题其实在小学时就已经讨论过了），用严谨的方法说明，让学生的知识体系更加完整，也凸显了二次函数的应用价值。
简单的变式，让学生巩固用二次函数解决实际问题的过程步骤。
在原题的基础上进一步变式，让学生明确自变量取值范围在函数问题中的重要性。
二.
师生互动
探索研究
问题二：
某商场将进价40元一个的某种商品按55元一个售出时，能卖出100个，已知这种商品每降价一元，销量增加20个，为赚得最大利润，售价应定为多少？最大利润是多少？
如何设未知数？
设降价x元，利润为y元
当时，
答：定价50元时，利润最大，为2000元。
练习巩固：
某商场销售某种品牌的牛奶,已知进价为每箱40元.商场按每箱50元销售,平均每天可售出90箱.市场调查发现，牛奶价格每箱每上涨1元,平均每天少销售3箱.商场计划通过涨价获得更高的利润。设每箱牛奶上涨x元。
(1)每箱牛奶上涨多少元时,平均每天获得的利润最大?最大利润是多少?
(2)有关部门规定每箱牛奶上涨的价格不能超过5元，此时每箱定价多少元才能获得最大利润，最大利润是多少？
问题三：
如图，已知AB=8，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P、C、E在一条直线上，，M，N分别为对角线AC，BE的中点，当点P在线段AB上移动时，点M，N之间的距离最短为_____.
设间接未知数，设降价x元。
学生口述函数表达式，全班合作，共同得到答案。
学生进行练习巩固，做到对此类问题的熟练掌握。
在教师的引导下，解决问题
利润问题在二次函数应用中非常常见，学生之前有一定的基础，因此问题二难度不大。
此练习的（2）涉及到非顶点处取最值的问题，提高学生融会贯通、举一反三的能力。
在几何问题的模型下建立二次函数的表达式，感受二次函数的应用广泛性。
三、
归纳总结
知识回顾
归纳常见的二次函数应用问题
几个注意点：二次函数自变量的取值范围、最值的取值情况分析。
思考总结
提高学生的反思意识
授后小记
对于实际问题，最关键的是如何从实际问题中抽象出函数关系，并利用数学知识得到问题的解。本节课涉及的问题难度不大，因此学生可以较好掌握。在习题中要注意学生对知识的灵活应用。