初中数学北师大版八年级下册第六章平行四边形综合与测试复习ppt课件

展开

这是一份初中数学北师大版八年级下册第六章平行四边形综合与测试复习ppt课件，共16页。PPT课件主要包含了平行线的性质，比一比，练一练，技能训练，综合运用技能比拼等内容，欢迎下载使用。

学习目标理解平行线的判定和平行线性质的区别与联系；能运用平行线的判定和性质进行综合推理，并规范推理过程；提高分析问题和解决问题的能力，培养推理能力和有条理的表达能力；
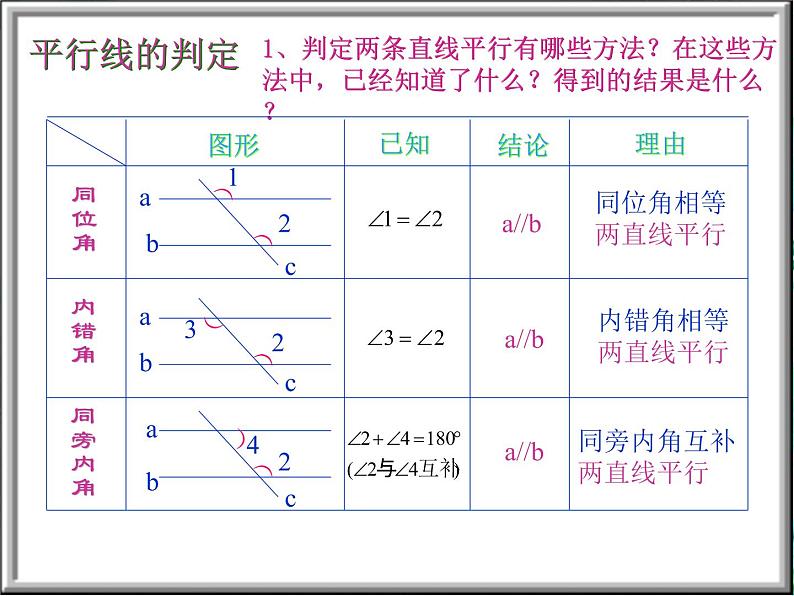
1、判定两条直线平行有哪些方法？在这些方法中，已经知道了什么？得到的结果是什么？
同旁内角互补两直线平行
区别：条件与结论互换，即：已知平行用性质，证明平行用判定。
一、平行线的判定方法：
同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；
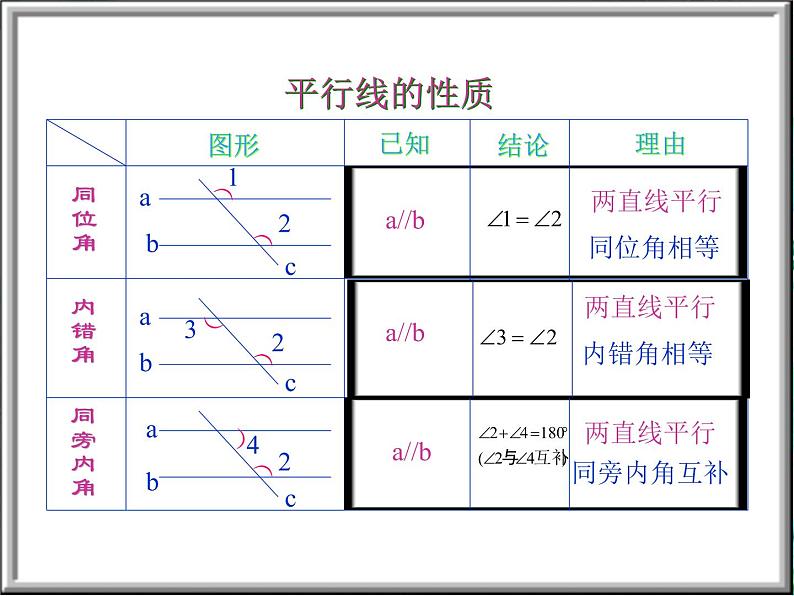
两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补。
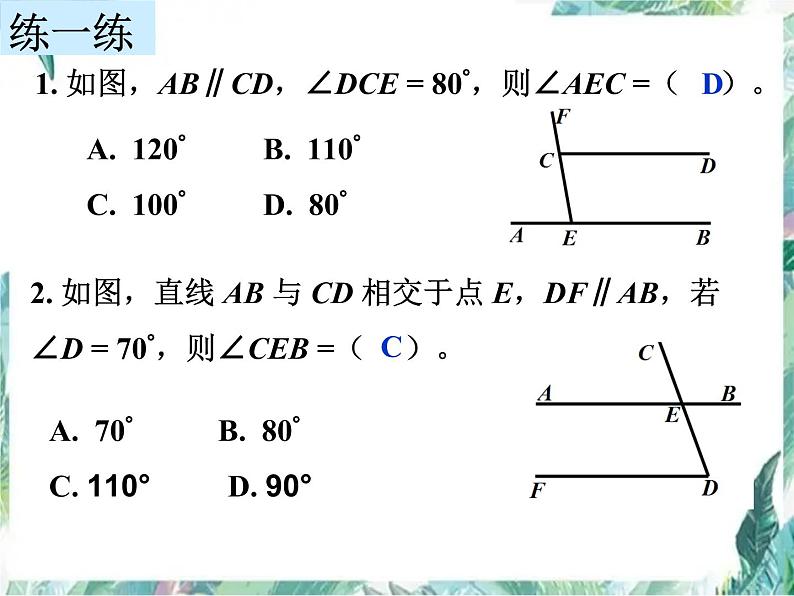
1. 如图，AB∥CD，∠DCE = 80°，则∠AEC =（）。
A. 120° B. 110°C. 100° D. 80°
2. 如图，直线 AB 与 CD 相交于点 E，DF∥AB，若∠D = 70°，则∠CEB =（）。
A. 70° B. 80°C. 110° D. 90°
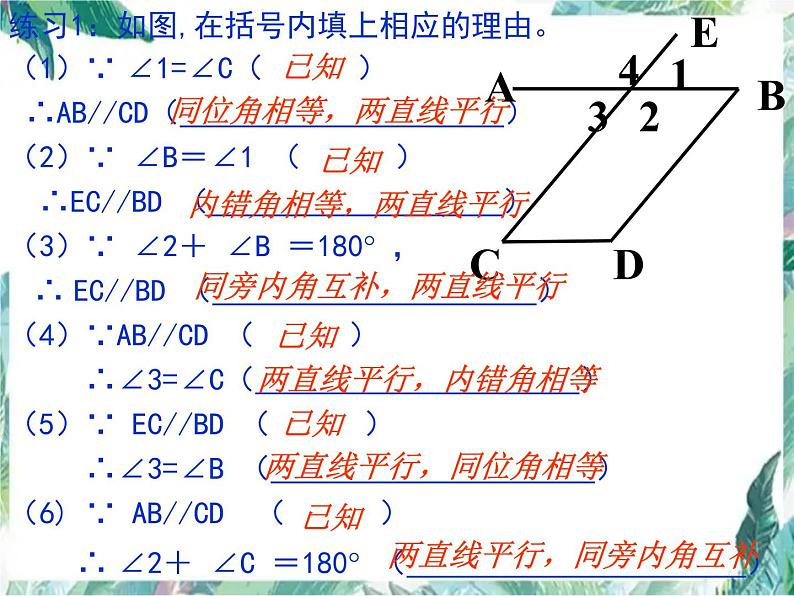
练习1：如图,在括号内填上相应的理由。（1）∵ ∠1=∠C（） ∴AB//CD（）（2）∵ ∠B＝∠1 （） ∴EC//BD （）（3）∵ ∠2＋ ∠B ＝180 ， ∴ EC//BD （）（4）∵AB//CD （） ∴∠3=∠C（）（5）∵ EC//BD （） ∴∠3=∠B （）（6) ∵ AB//CD （） ∴ ∠2＋ ∠C ＝180 （）
同位角相等，两直线平行
两直线平行，同旁内角互补
同旁内角互补，两直线平行
内错角相等，两直线平行
两直线平行，同位角相等
两直线平行，内错角相等
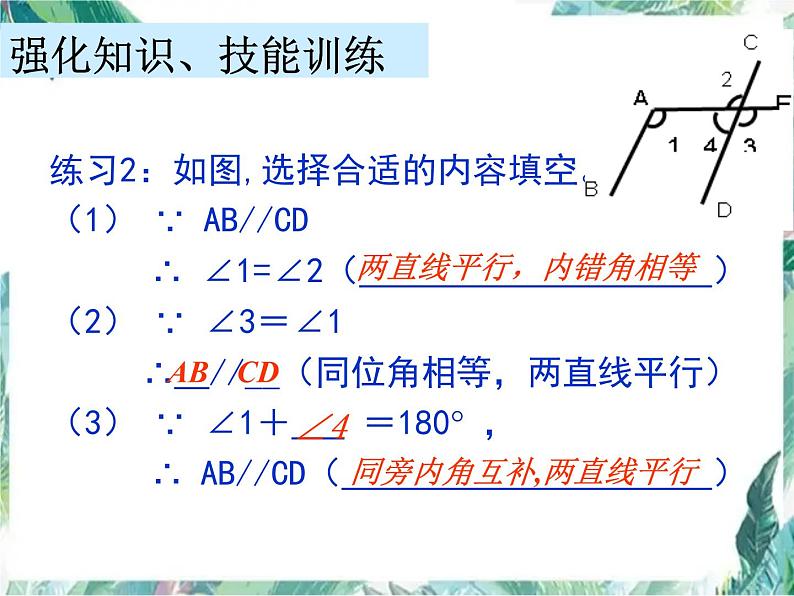
练习2：如图,选择合适的内容填空。（1） ∵ AB//CD ∴ ∠1=∠2（）（2） ∵ ∠3＝∠1 ∴ //__（同位角相等，两直线平行）（3） ∵ ∠1＋＝180 ， ∴ AB//CD（）
同旁内角互补,两直线平行
1.如图, 若∠3=∠4，则 ∥ ；
若AB∥CD, 则∠ =∠ 。
2.如图，∠D=70°，∠C= 110°,∠1=69°，则∠B= ·
3 . 如图,c⊥a,c⊥b,∠1=700，则∠2= .
如果,c⊥a,c⊥b,则a //b即：垂直于同一条直线的两条直线平行
1、已知，如图直线AB、CD被直线EF所截，且∠1+∠2=180°求证：AB//CD
∴ ∠3=∠2 ( )
证明： ∵∠1+∠3=180°( )
∠1+∠2=180°( )
∴AB//CD( )
2.如图已知AD∥BC,且DC⊥AD于D.
(1)DC与BC有怎样的位置关系？说说你的理由。(2)你能说明∠1+∠2=180°吗？
（1）DC⊥BC 理由：
∵ DC⊥AD ( )∴ ∠3=90° ( )
又∵ AD∥BC ( ) ∴ ∠3=∠2=90°( )
(2)证明： ∵ AD∥BC ( )
∴∠2+∠4=180°( )
又 ∵ ∠1=∠4( )
∴∠1+∠2 =180°( )
3、已知∠DAC= ∠ACB, ∠D+∠DFE= 180°, 求证:EF//BC
又∵ ∠D+∠DFE= 180°( )
证明： ∵ DAC= ∠ACB ( )
∴ DA//BC( )
∴ DA//EF( )
∴ EF//BC( )
平行于同一条直线的两条直线平行
（1）平行线的判定与性质的区别？（2）在解决问题的过程中，何时使用平行线的判定，何时使用平行线的性质？（3）当已知条件中两个角没有特殊位置时，怎样处理？
我学会了------- 我弄懂了------- 还有------

相关课件更多