初中数学苏科版九年级下册5.2 二次函数的图象和性质教案设计
展开5.2 二次函数的图像和性质(4)
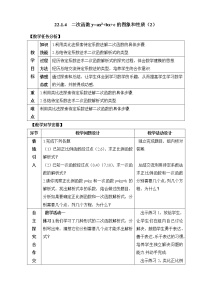
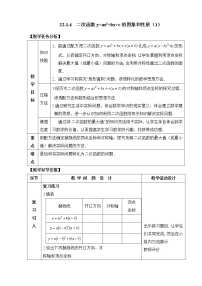
教学目标:会用描点法画函数y=a(x+m)2+k(a≠0)的图像;会用平移变换解释函数y=a(x+m)2+k与函数y=ax2+k、y=a(x+m)2、y=ax2(a≠0)的图像之间的关系;会用配方法确定二次函数图像的顶点坐标、对称轴,根据对称性列表、描点、画图,并确定函数的最大值或者最小值;进一步体会数学研究问题由具体到抽象、特殊到一般的思想方法.
教学重点:会用平移变换解释函数y=a(x+m)2+k与y=ax2(a≠0)的图像之间的关系;会用配方法确定二次函数图像的顶点坐标、对称轴、函数的最值,根据对称性列表、描点、画出函数图像.
教学难点:感受图形的运动变化与图形上点的坐标变化之间的关系,体验由具体到抽象、特殊到一般的研究问题的方法.
教学过程:
一、复习
1、函数y=x2+2的图像与y=x2的图像有什么关系?
2、函数y=(x+3)2的图像和y=x2的图像有什么关系?
要求:回顾上节课所学函数y=ax2+k、y=a(x+m)2的图像和函数y=ax2(a≠0)图像的关系,为本节课学习打下基础.
二、探索活动
画图与观察
画函数y=x2、y=(x+3)2和y=(x+3)2+2的图像.
1.填表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2[来源:学,科,网Z,X,X,K] | 3 | … |
y=x2 | … |
|
|
| [来源:学§科§网] |
|
|
|
| … |
y=(x+3)2 | … |
|
|
|
|
| [来源:Z,xx,k.Com] |
| … | |
y=(x+3)2+2 | … |
|
|
|
|
| [来源:Zxxk.Com] |
|
| [来源:学+科+网] |
2.画图:在平面直角坐标系中,描点并画出函数y=x2、y=(x+3)2和y=(x+3)2+2的图像;
要求:引导学生观察:(1)能说出函数y=(x+3)2+2的图像的形状吗?(2)函数y=(x+3)2+2的图像与函数y=(x+3)2和y=x2的图像有什么联系?(3)根据图像,你能得出函数y=(x+3)2+2图像的性质吗?
3.思考:函数y=x2+2x+3的图像是抛物线吗?它与函数y=(x+1)2+2有何关系?
通过配方发现:y=x2+2x+3
=(x+1)2+2
因此得出函数y=x2+2x+3的图像是抛物线.
要求:教师板书配方过程,学生模仿写一遍,学生有了上节课的基础,能猜想出函数
y=(x+3)2+2可以由函数y=x2通过平移变换得到.
三、总结与归纳
思考:(1)函数y=a(x+m)2+k的图像与y=ax2(a≠0)的图像有什么关系?
(2)函数y=a(x+m)2+k(a≠0)有什么性质?
要求:学生先交流、尝试概括,师生共同总结出结论:(1)函数y=a(x+m)2+k的图像可以看成由函数y=ax2(a≠0)的图像平移得到,当k>0时,向上平移k个单位,当k<0时,向下平移-k个单位;当m>0时,向左平移m个单位,当m<0时,向右平移-m个单位.(2)函数y=a(x+m)2+k顶点坐标是
(-m,k),对称轴是过(-m,k)与y轴平行的直线.学生相互交流、补充,逐步完善函数y=a(x+m)2+k的性质,函数的增减性、开口方向和最大(小)值要分a>0和a<0来讨论.
四、转化与思考
(1)你能将函数y=-x2-4x-5转化为y=a(x+m)2+k的形式吗?并画出它的图像,指出它的开口方向、顶点坐标、对称轴、最大(小)值.
要求:学生自己通过配方转化
(2)如何将二次函数y=ax2+bx+c转化y=a(x+m)2+k的形式?
二次函数y=ax2+bx+c(a≠0)可以转化为y=a(x+)2+;由此可知,二次函数y=ax2+bx+c(a≠0)的图像是抛物线,顶点坐标为(-,),对称轴是过顶点与y轴平行的直线.
函数的增减性、开口方向和最大(小)值要分a>0和a<0来讨论.
根据公式y=a(x+)2+,探讨和在二次函数y=ax2+bx+c(a≠0)图像和性质中的几何意义和代数意义,重点不是公式的记忆,而是配方的方法.
要求:教师板书全过程
五、总结
函数y=a(x+m)2+k与y=ax2(a≠0)的图像之间的关系
要求:学生会用平移变换解释函数y=a(x+m)2+k与y=ax2(a≠0)的图像之间的关系
六、课堂练习
用配方法把下列二次函数化成顶点式,并说出它的图像性质:
① ②
七、课后作业
1.画出二次函数的图像,并指出它的开口方向、顶点坐标、对称轴、
最大值或最小值和增减性。
鲁教版 (五四制)九年级上册2 二次函数教案设计: 这是一份鲁教版 (五四制)九年级上册2 二次函数教案设计,共3页。教案主要包含了自主探索等内容,欢迎下载使用。
鲁教版 (五四制)九年级上册2 二次函数教案设计: 这是一份鲁教版 (五四制)九年级上册2 二次函数教案设计,共6页。
苏科版九年级下册5.2 二次函数的图象和性质教学设计: 这是一份苏科版九年级下册5.2 二次函数的图象和性质教学设计,共4页。