2022北京顺义区高三下学期第二次统练数学试题含答案

顺义区2022届高三第二次统练

数学试卷

第一部分（选择题共40分）

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

1. 函数的定义域为（）

A.  B.  C.  D.

【1题答案】

【答案】A

2. 如图，在复平面内，复数对应的点为，则复数（）

A.  B.  C.  D.

【2题答案】

【答案】D

3. 展开式中的常数项为（）

A.  B.  C. 15 D. 30

【3题答案】

【答案】C

4. 已知双曲线的一个焦点为，则双曲线的一条渐近线方程为（）

A.  B.  C.  D.

【4题答案】

【答案】A

5. 设等比数列的前项和为，公比为.若，则（）

A.  B.  C.  D.

【5题答案】

【答案】C

6. 为了了解居民用电情况，通过抽样，获得了某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如下图.该样本数据的55%分位数大约是（）

A.  B.  C.  D.

【6题答案】

【答案】C

7. 在中，，则“”是“”的（）

A. 充分不必要条件 B. 必要不充分条件

C. 充分必要条件 D. 既不充分也不必要件

【7题答案】

【答案】B

8. 已知圆截直线所得弦的长度为2，那么实数的值为（）

A.  B.  C.  D.

【8题答案】

【答案】D

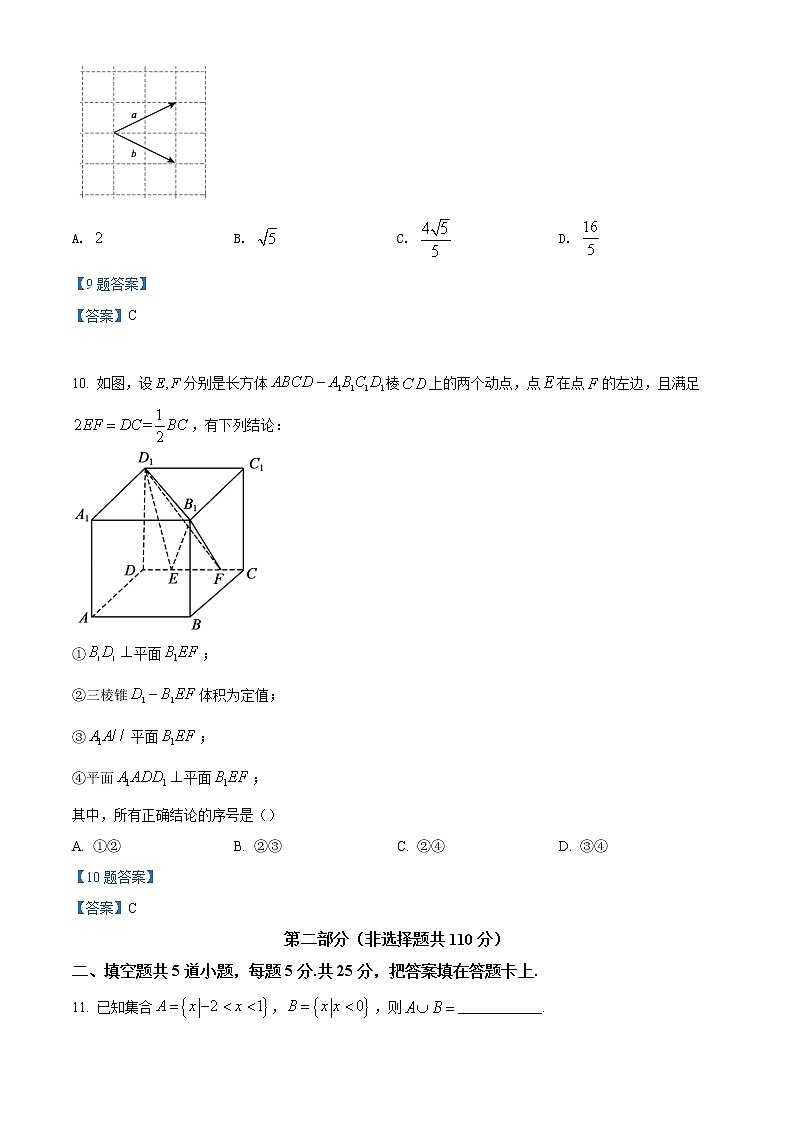
9. 已知向量，，在正方形网格中的位置如图所示．若网格纸上小正方形的边长为，则的最小值是（）

A.  B.  C.  D.

【9题答案】

【答案】C

10. 如图，设分别是长方体棱上的两个动点，点在点的左边，且满足，有下列结论：

①平面；

②三棱锥体积为定值；

③平面；

④平面平面；

其中，所有正确结论的序号是（）

A. ①② B. ②③ C. ②④ D. ③④

【10题答案】

【答案】C

第二部分（非选择题共110分）

二、填空题共5道小题，每题5分.共25分，把答案填在答题卡上.

11. 已知集合，，则____________.

【11题答案】

【答案】

12. 已知函数，若，则_____________.

【12题答案】

【答案】4

13. 已知抛物线的焦点为，点在抛物线上，垂直抛物线准线于点.若为等边三角形，则点的横坐标为___________，的面积是________________.

【13题答案】

【答案】    ①. 3；    ②. .

14. 已知是定义在上的函数，其值域为，则可以是________.（写出一个满足条件的函数表达式即可）

【14题答案】

【答案】

15. 向量集合，对于任意，，以及任意，都有，则称集合是“凸集”，现有四个命题：

①集合是“凸集”；

②若为“凸集”，则集合也是“凸集”；

③若都是“凸集”，则也是“凸集”；

④若都是“凸集”，且交集非空，则也是“凸集”．

其中，所有正确的命题的序号是_____________________．

【15题答案】

【答案】①②④

三、解答题共6道题，共85分.解答应写出文字说明，证明过程或演算步骤.

16. 已知函数.

（1）求在区间上的最大值和最小值；

（2）设，求的最小正周期.

【16题答案】

【答案】（1）

（2）

18. 如图，在正方体中，为的中点.

（1）过点作出一条与平面平行的直线，并说明理由；

（2）求直线与平面所成角的正弦值.

【18题答案】

【答案】（1）答案见解析；

（2）.

20. 为了解顺义区某中学高一年级学生身体素质情况，对高一年级的（）班（）班进行了抽测，采取如下方式抽样：每班随机各抽名学生进行身体素质监测.经统计，每班名学生中身体素质监测成绩达到优秀的人数散点图如下：（轴表示对应的班号，轴表示对应的优秀人数）

（1）若用散点图预测高一年级学生身体素质情况，从高一年级学生中任意抽测人，求该生身体素质监测成绩达到优秀概率；

（2）若从以上统计的高一（）班的名学生中抽出人，设表示人中身体素质监测成绩达到优秀的人数，求的分布列及其数学期望；

（3）假设每个班学生身体素质优秀的概率与该班随机抽到的名学生的身体素质优秀率相等.现在从每班中分别随机抽取名同学，用“”表示第班抽到的这名同学身体素质优秀，“”表示第班抽到的这名同学身体素质不是优秀．写出方差的大小关系（不必写出证明过程）．

【20题答案】

【答案】（1）

（2）分布列见解析，数学期望

（3）

22. 已知椭圆过定点，离心率.

（1）求椭圆的标准方程；

（2）斜率为的直线与椭圆交于两点，为坐标原点，求面积的最大值及此时直线的方程.

【22题答案】

【答案】（1）

（2）1，

24. 若函数.

（1）判断方程解的个数，并说明理由；

（2）当，设，求的单调区间.

【24题答案】

【答案】（1）仅有一个，理由见解析；

（2）答案见解析.

26. 设正整数数列满足．

（1）若，请写出所有可能的取值；

（2）记集合，证明：若集合存在一个元素是3的倍数，则的所有元素都是3的倍数；

（3）若为周期数列，求所有可能的取值.

【26题答案】

【答案】（1），，

（2）证明见解析（3）