数学必修 第二册6.2 平面向量的运算精品ppt课件

这是一份数学必修 第二册6.2 平面向量的运算精品ppt课件，文件包含6242平面向量的运算pptx、6242平面向量的运算docx等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。
注意：两个向量a与b的数量积是一个实数，不是一个向量.
已知两个非零向量a与b，它们的夹角为θ，我们把数量|a||b|csθ叫做向量a与b的数量积(或内积)，记作a∙b,即a∙b = |a||b|csθ .
两个向量的数量积是两个向量之间的一种运算.既然是一种运算，该遵循什么样的运算律呢?
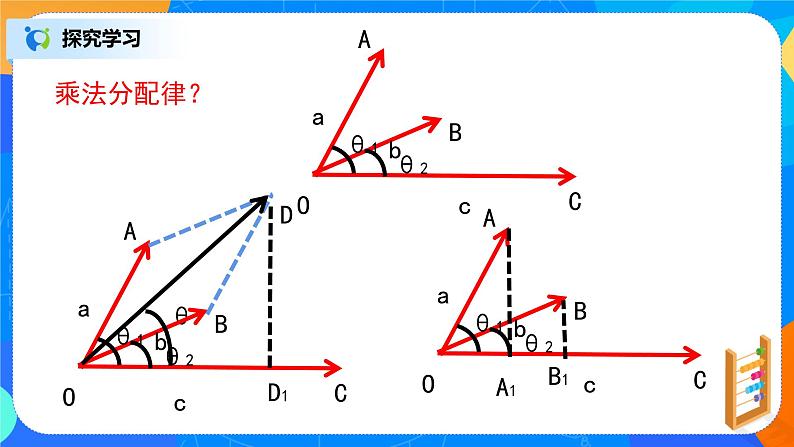
乘法交换律？乘法结合律？乘法分配律？
证明：a·b= |a||b| cs θ b·a=|b| |a|csθ 则a·b=b·a
证明：(a·b) ·c 表示一个与c共线的向量， 而a·(b·c)表示一个与a共线的自量， c与a不一定共线， 则(a·b) ·c=a·(b·c)，一般情况下不 会成立.
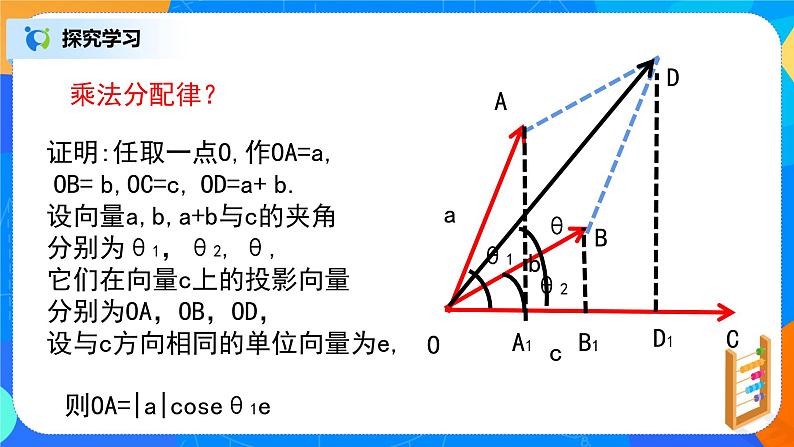
证明:任取一点O,作OA=a, OB= b,OC=c, OD=a+ b. 设向量a,b,a+b与c的夹角分别为θ1，θ2, θ,它们在向量c上的投影向量分别为OA，OB，OD，设与c方向相同的单位向量为e,
则OA=|a|cseθ1e
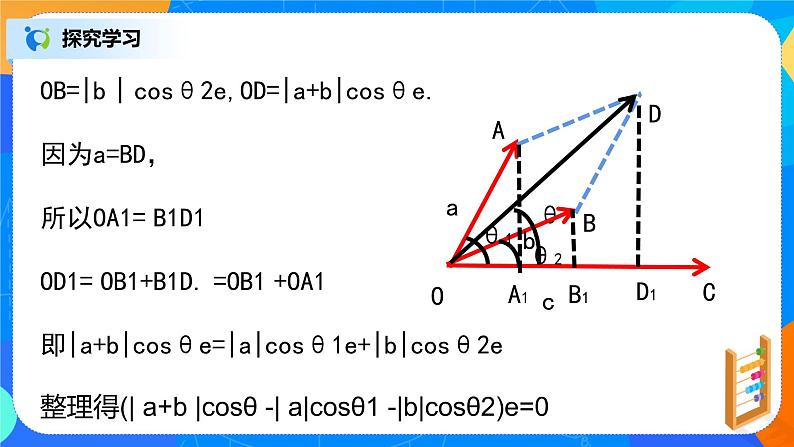
OB=|b | csθ2e,OD=|a+b|csθe. 因为a=BD，所以OA1= B1D1 OD1= OB1+B1D. =OB1 +OA1 即|a+b|csθe=|a|csθ1e+|b|csθ2e整理得(| a+b |csθ -| a|csθ1 -|b|csθ2)e=0
| a+b |csθ -|a|csθ1 -|b|csθ2=0 即| a+b|csθ = | a|csθ 1+| b| csθ2. 所以 | a+b||c|csθ = |a||c|csθ1 +|b||c| csθ2.因此（a+b）·c= a·c +b·c
向量结合律与数乘运算及向量数量积的混合运算有什么关系？
(λa) ·b=λ(a·b)=a·(λ  b)    (λ 为实数)
分（λ=0，λ＜0，λ＞0三种情况讨论）
证明：设向量a与b的夹角カθ. (1) 当λ=0吋，0·b=0·(a·b)=a·0=0. (2) 当λ>0时， λa与b，a与λb的夹角都为θ. 所以(λa) · b= |λa||b|csθ =λ | a||b|csθλ (a· b)= λ | a||b|csθ = a· (λb) = |a||λb|csθ=λ | a||b|csθ则(λa) · b= λ (a· b)= a· (λb)
(3)当λ