高中数学人教A版 (2019)必修 第二册第六章 平面向量及其应用6.2 平面向量的运算优秀ppt课件

这是一份高中数学人教A版 (2019)必修 第二册第六章 平面向量及其应用6.2 平面向量的运算优秀ppt课件，文件包含6243平面向量的运算pptx、6243平面向量的运算docx等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。
两个向量可以相加，并且两个向量的和还是一个向量.一般地，求两个向量和的运算，叫做向量的加法.
向量a加上b的相反向量，叫做a与b的差，即a-b=a+(-b).求两个向量差的运算叫做向量的减法.
一般地，我们规定实数λ与向量a的积是一个向量，这种运算叫做向量的数乘，记作λ a
已知两个非零向量a与b，它们的夹角为θ，我们把数量|a| ∙ |b|csθ叫做向量a与b的数量积(或内积)，记作a∙b,即a∙b = |a||b|csθ .
例1若|a|=1,|b|= 2,向量a与向量b的夹角为120°
( 1)求a∙b. ( 2)求|a+b|. (3) 求向量a与向量a+b的夹角.
对于(1)求a · b，直接代入公式a · b=|a||b| cs θ. 对于(2)求|a+b| 应该联想性质|a+b|^2=(a+b) ^2. 对于(3) 求向量a与向量a+b的夹角利用公式csθ=(a·(a+b))/(|a||a+b|）
已知:|a|=1,|b|=2, θ=120 °
（1） a·b=|a|·|b|cs120 ° =1 ×2(-1/2)=-1. （2）因为|a+b|^2=(a+b)^2  =a^2+ 2a·b+b^2 =1-2+4=3 所以|a +b|=√3. （3） 因为a·(a+b)=a^2 +a·b=1-1=0.  则csθ1=(a·(a+b))/(|a||a+b|）=0 则a与（a+b）的夹角θ1=90 °
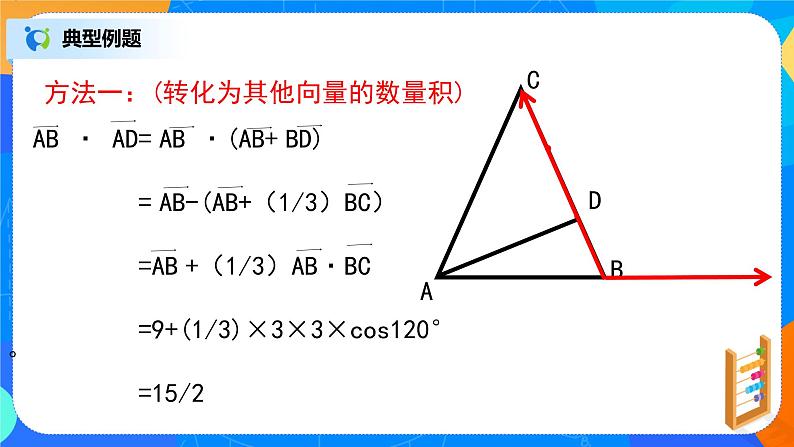
方法一：(转化为其他向量的数量积)
方法二: (利用投影向量)
数量积的几种方法的适用条件： 定义法:数量积定义，适用条件是已知向量的模与夹角。 转化法:适用条件是所求数量积，可以转化为已知模和夹角的向量。几何法:适用条件是易求得投影向量。
已知a，b,是单位向量,a·b=0.若向量c满足|c-a-b|=1，求|c|的取值范围
利用转化法、几何法、放缩法求解向量中的最值问题.
定义法、转化法、投影法等.
必做题：综合运用14.15选作题：拓展探索22.23