人教A版 (2019)必修 第二册6.3 平面向量基本定理及坐标表示优质课件ppt

这是一份人教A版 (2019)必修 第二册6.3 平面向量基本定理及坐标表示优质课件ppt，文件包含635平面向量基本定理及坐标表示pptx、635平面向量基本定理及坐标表示docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

平面向量的基本定理及其坐标表示
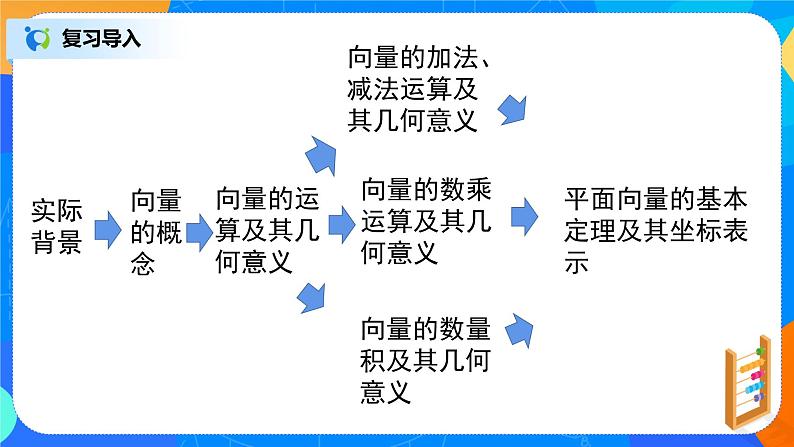
向量的运算及其几何意义
向量的加法、减法运算及其几何意义
向量的数乘运算及其几何意义
向量的数量积及其几何意义
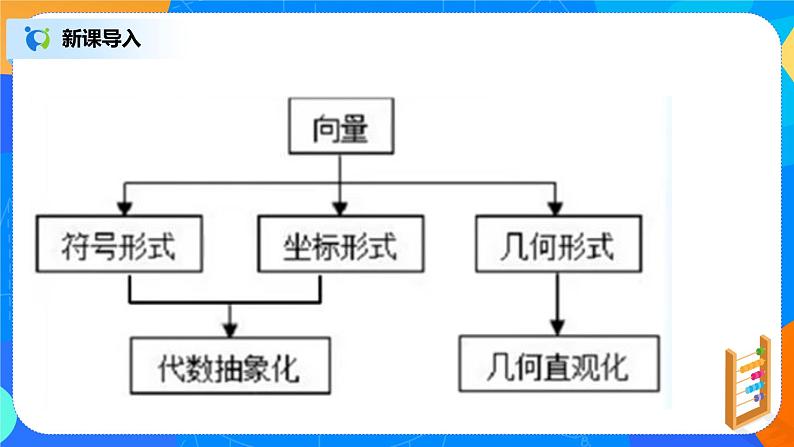
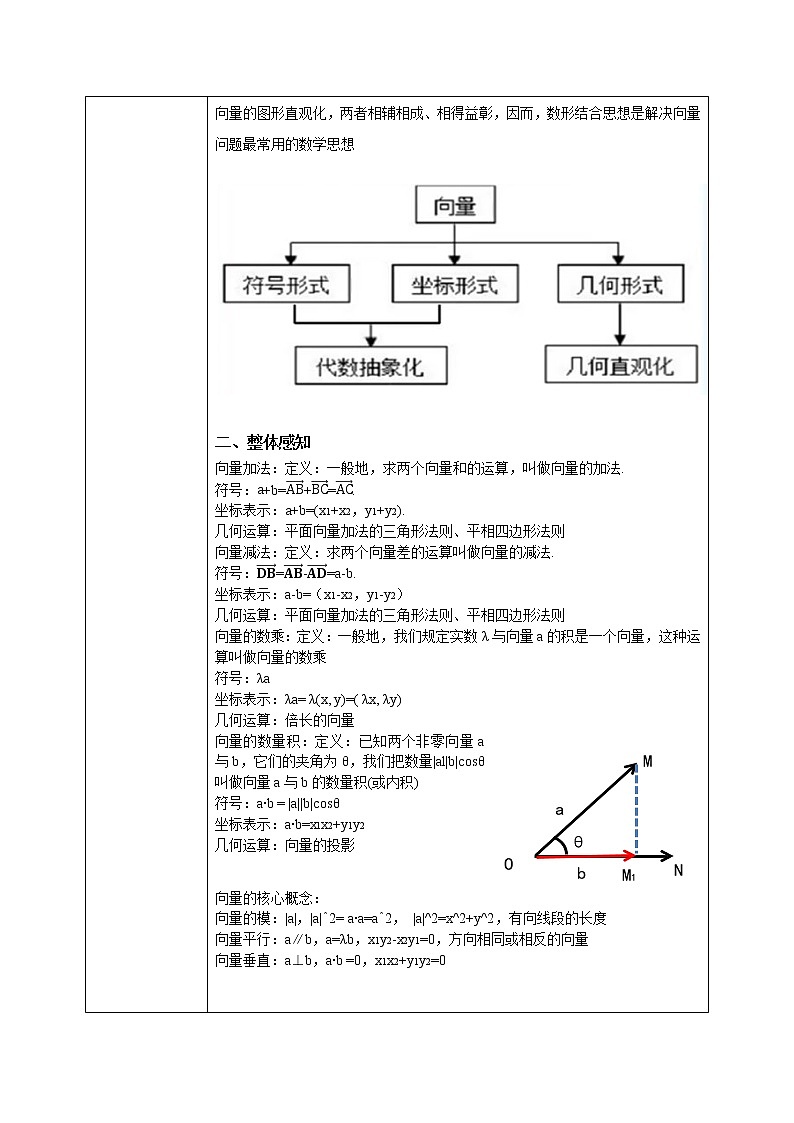
事实上，平面向量有着清晰的三条主线:符号形式、几何形式、坐标形式，符号形式与坐标形式反映了向量的代数抽象化，几何形式反映了向量的图形直观化，两者相辅相成、相得益彰，因而，数形结合思想是解决向量问题最常用的数学思想
定义：一般地，求两个向量和的运算，叫做向量的加法.
坐标表示：a+b=(x1+x2，y1+y2).几何运算：平面向量加法的三角形法则、平相四边形法则
坐标表示：a-b=（x1-x2，y1-y2）几何运算：平面向量加法的三角形法则、平相四边形法则
定义：求两个向量差的运算叫做向量的减法.
定义：一般地，我们规定实数λ与向量a的积是一个向量，这种运算叫做向量的数乘符号：λa坐标表示：λa= λ(x, y)=( λx, λy)几何运算：倍长的向量
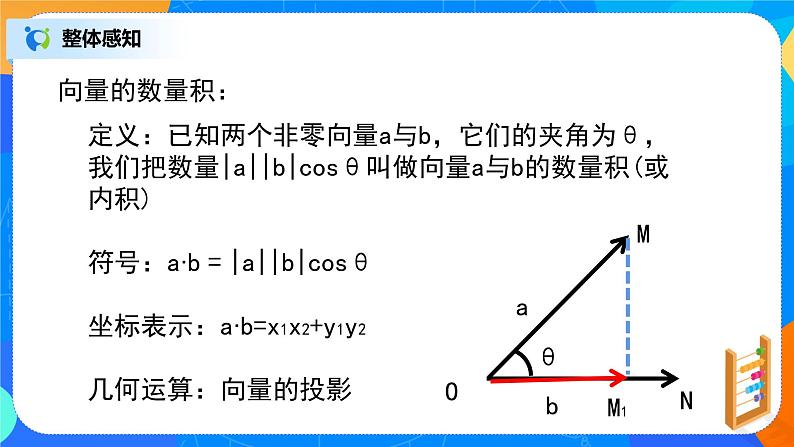
定义：已知两个非零向量a与b，它们的夹角为θ，我们把数量|a||b|csθ叫做向量a与b的数量积(或内积)符号：a∙b = |a||b|csθ 坐标表示：a∙b=x1x2+y1y2几何运算：向量的投影
向量的模：|a|，|a|^2= a∙a=a^2， |a|^2=x^2+y^2，有向线段的长度向量平行：a∥b，a=λb，x1y2-x2y1=0，方向相同或相反的向量向量垂直：a⊥b，a∙b =0，x1x2+y1y2=0
例题1:已知两个非零向量a，b满足|a+b|=|a-b|求证a⊥b.
因为|a+b|=|a-b|所以|a+b|^2=|a-b|^2所以(a+b)^2 =(a-b)^2所以a^2+ 2a∙b+b^2=a^2-2a∙b+b^2所以4a∙b= 0.又因为a,b是非零向量，所以a⊥b.
设a= (x1，,y1),b= (x2,y2)所以a+b=(x1+x2，y1+y2) a-b=(x1-x2，y1-y2)又因为|a+b|=|a-b|所以(x1+x2)^2 +( y1+y2)^2=(x1-x2) ^2+( y1-y2)^2整理得x1x2 + y1y2 =0. 所以a⊥b.
本题小结: (1)深刻理解知识; (2)抓住问题，从符号、坐标和几何三种多角度去思考问题; (3) 对比不同解法的异同，找到解决问题的最佳方法。
(1) 抓住问题的特点，从符号、坐标和几何三种多角度来思考问题; (2)反思不同的解法，找到解决问题的切入口; (3) 不同的思考角度，得到不同的解法，需要不同的知识储备，领略不同的风景