高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直复习课件ppt

这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直复习课件ppt，共11页。PPT课件主要包含了知识回顾，直二面角，课堂互动，证明1法1，∴BG⊥平面PAD等内容，欢迎下载使用。
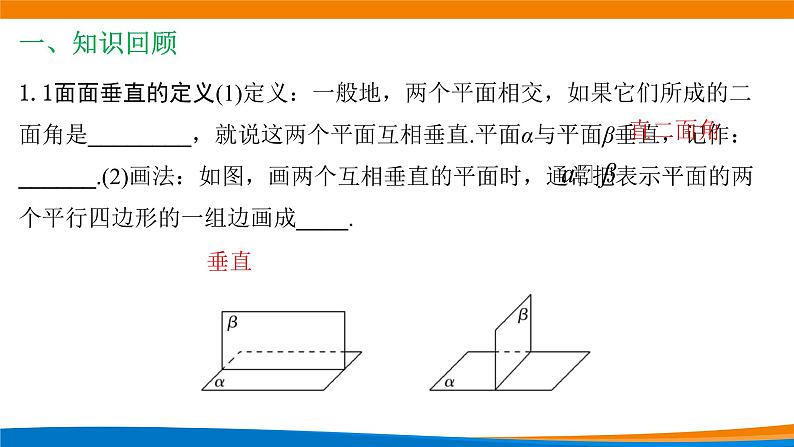
1.1面面垂直的定义(1)定义：一般地，两个平面相交，如果它们所成的二面角是________，就说这两个平面互相垂直.平面α与平面β垂直，记作：______.(2)画法：如图，画两个互相垂直的平面时，通常把表示平面的两个平行四边形的一组边画成____.
1.2【微训练】1.对于直线m，n和平面α，β，能得出α⊥β的一个条件是(　　)A.m⊥n，m∥α，n∥β B.m⊥n，α∩β＝m，n⊂αC.m∥n，n⊥β，m⊂α D.m∥n，m⊥α，n⊥β
平面与平面垂直的判定定理
2.判断题(1)若平面α不垂直于平面β，则平面α内一定不存在直线垂直于平面β.( )(2)若平面α⊥平面β，则平面α内一定存在直线平行于平面β.( )(3)若平面α⊥平面β，则平面α内所有直线都垂直于平面β.( )
平面与平面垂直的性质定理
题型一　求二面角的大小如图所示，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上的一点，且PA＝AC，求二面角P－BC－A的大小.
解　∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC.
∵AB是⊙O的直径，且点C在圆周上，∴AC⊥BC.
又∵PA∩AC＝A，PA，AC⊂平面PAC，∴BC⊥平面PAC.
而PC⊂平面PAC，∴PC⊥BC.
又∵BC是二面角P－BC－A的棱，∴∠PCA是二面角P－BC－A的平面角.
由PA＝AC知，△PAC是等腰直角三角形，∴∠PCA＝45°，
即二面角P－BC－A的大小是45°.
题型二　平面与平面垂直的证明
如图，在四棱锥P­ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点．(1)求证：BD⊥平面PAC；(2)若∠ABC＝60°，求证：平面PAB⊥平面PAE.
证明 （1）菱形ABCD中，BD⊥AC.
PA⊥平面ABCD， 平面ABCD， PA⊥BD.
题型三　平面与平面垂直的性质及应用如图所示，四棱锥P－ABCD中，底面ABCD是∠DAB＝60°且边长为a的菱形，侧面PAD为正三角形， 其所在平面垂直于底面ABCD，G为AD边的中点.求证：
(1)BG⊥平面PAD；(2)AD⊥PB；(3)求点D到面PAB的距离.
又平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，BG⊂平面ABCD，
∵四边形ABCD是菱形且∠DAB＝60°，∴△ABD是正三角形，∴BG⊥AD.
证明　(1)(法2)由题意知△PAD为正三角形，G是AD的中点，∴PG⊥AD.
又平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，PG⊂平面PAD，
∵PG⊥平面ABCD，BG⊂平面ABCD，∴PG⊥BG.
又∵四边形ABCD是菱形且∠DAB＝60°，∴△ABD是正三角形，∴BG⊥AD.
又AD∩PG＝G，AD，PG⊂平面PAD，∴BG⊥平面PAD.
(2)由(1)可知BG⊥AD，PG⊥AD，BG∩PG＝G，BG，PG⊂平面PBG，∴AD⊥平面PBG，
又PB⊂平面PBG，所以AD⊥PB.
(3)由(1)可知PG⊥平面ABCD，∴PG是三棱锥P-ABD的高，PG= .
设点D到面PAB的距离为h,
即：点D到面PAB的距离为