高中数学6.3 球的表面积和体积集体备课课件ppt

这是一份高中数学6.3 球的表面积和体积集体备课课件ppt，共37页。PPT课件主要包含了学习目标，学习重难点，S’S，S’0，r’r，r’0等内容，欢迎下载使用。

重点：球的表面积和体积公式.难点：与球相关的简单组合体的表面积和体积的计算。
1.掌握球的截面特征，了解切线的概念和性质；2.掌握球的表面积体积的计算公式，并能运用公式解决简单的 实际问题。
1.柱体、锥体、台体的体积公式
一、 复习柱体、锥体、台体的表面积和体积
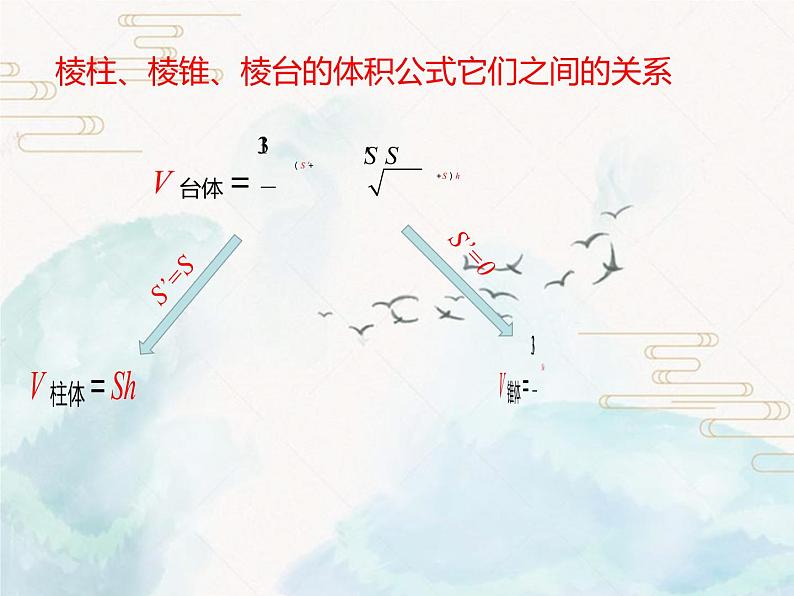
棱柱、棱锥、棱台的体积公式它们之间的关系
棱锥及棱台的表面积计算常借助斜高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形（或梯形）求解.
棱柱、棱锥、棱台的表面积的求解方法:
二. 圆柱、圆锥、圆台的表面积和体积
S圆柱＝2πr（r+l） （r是底面半径，l是母线长），S圆锥＝πr（r+l） （r是底面半径，l是母线长）， S圆台＝π（r′2+r2+r′l+rl） （r′，r分别是上、下底面半径，l是母线长）.
1. 圆柱、圆锥、圆台的表面积
圆柱、圆锥、圆台的表面积公式之间的关系
2. 圆柱、圆锥、圆台的体积
例3、已知圆台的上底面半径是2，下底面半径是3，截得此圆台的圆锥的高为6，则此圆台的表面积为多少？
练习1.把长和宽分别为6和3的矩形卷成一个圆柱的侧面，求这个圆柱的体积.
解决圆柱、圆锥、圆台的表面积问题，要利用好空间几何体的轴截面及侧面展开图，借助平面几何知识，求得所需几何要素，代入公式求解即可，基本步骤如下：（1）得到空间几何体的平面展开图.（2）依次求出各个平面图形的面积.（3）将各平面图形的面积相加.
圆柱、圆锥、圆台的表面积的求解步骤:
注：求台体的表面积时，关键在于 “还台为锥”。
三. 球的表面积和体积
【解】　正方体的表面积为4×4×6＝96（cm2），圆柱的侧面积为2π×1×4＝8π（cm2），圆柱的底面积为2π cm2，则挖洞后的几何体的表面积为96+8π-2π＝（96+6π）（cm2）.
例7、已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为( ) A. 36πB. 64π C. 144π D. 256π
例8.一个球内有相距9 cm的两个平行截面，它们的面积分别为49π cm2和400π cm2，求球的表面积.
【解】　分两种情况：（1）当截面在球心的同侧时，如图所示，由截面性质知，AO1∥BO2，O1，O2为两截面圆的圆心，且OO1⊥AO1，OO2⊥BO2. ∵ π·O2B2＝49π，∴ O2B＝7 cm. ∵ π·O1A2＝400π，∴ O1A＝20 cm.设球的半径为R cm，OO1＝x cm，则OO2＝（x+9） cm.在Rt△OO1A中，R2＝x2+202.①在Rt△OO2B中，R2＝72+（x+9）2.②联立①②，解得x＝15，R＝25.∴ S球＝4πR2＝2 500π（cm2），故球的表面积为2 500π cm2. 
（2）当截面在球心的两侧时，如图所示，由截面性质知，O1A∥ O2B，O1，O2分别为两截面圆的圆心，且OO1⊥AO1，OO2⊥BO2.∵ π·O2B2＝49π，∴ O2B＝7 cm.∵ π·O1A2＝400π，∴ O1A＝20 cm.设球的半径为R cm，OO1＝x cm，则OO2＝（9-x） cm.在Rt△OO1A中，R2＝x2+400.③在Rt△OO2B中，R2＝（9-x）2+49.④联立③④，解得x＝-15，不合题意，舍去.综上所述，球的表面积为2 500π cm2.
多面体的内切球与外接球问题
1.多面体的内切球（球在多面体内）
2.多面体的外接球（球在多面体外）①若一个多面体的每一个顶点都在一个球的球面上，则称这个球是该多面体的外接球.②求解多面体的外接球问题的关键是找到球心的位置（球心与多面体每个顶点的连线都是球的半径）.抓住球心到某个截面的距离d，利用公式R2＝r2+d2求解（其中R为球的半径，r为截面圆的半径）.
例2.有三个球，第一个球内切于正方体的六个面，第二个球与这个正方体的各条棱相切，第三个球过这个正方体的各个顶点，求这三个球的表面积之比.
解决与球相关的“切”“接”问题的关键