高考专题1 规范答题1 函数与导数

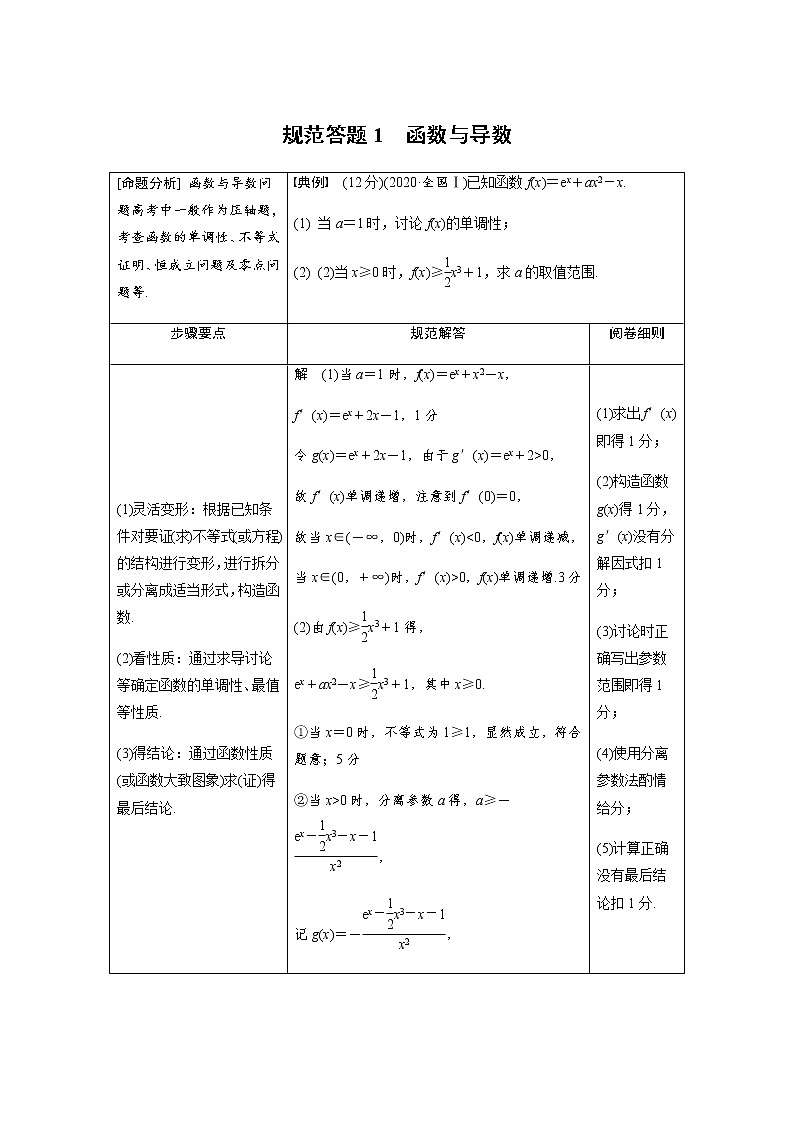
规范答题1　函数与导数[命题分析] 函数与导数问题高考中一般作为压轴题，考查函数的单调性、不等式证明、恒成立问题及零点问题等.典例　(12分)(2020·全国Ⅰ)已知函数f(x)＝ex＋ax2－x.(1)    当a＝1时，讨论f(x)的单调性；(2)    (2)当x≥0时，f(x)≥x3＋1，求a的取值范围.步骤要点规范解答阅卷细则(1)灵活变形：根据已知条件对要证(求)不等式(或方程)的结构进行变形，进行拆分或分离成适当形式，构造函数.(2)看性质：通过求导讨论等确定函数的单调性、最值等性质.(3)得结论：通过函数性质(或函数大致图象)求(证)得最后结论.解　(1)当a＝1时，f(x)＝ex＋x2－x，f′(x)＝ex＋2x－1，1分令g(x)＝ex＋2x－1，由于g′(x)＝ex＋2>0，故f′(x)单调递增，注意到f′(0)＝0，故当x∈(－∞，0)时，f′(x)<0，f(x)单调递减，当x∈(0，＋∞)时，f′(x)>0，f(x)单调递增.3分(2)由f(x)≥x3＋1得，ex＋ax2－x≥x3＋1，其中x≥0.①当x＝0时，不等式为1≥1，显然成立，符合题意；5分②当x>0时，分离参数a得，a≥－，记g(x)＝－，g′(x)＝－，7分令h(x)＝ex－x2－x－1(x≥0)，则h′(x)＝ex－x－1，令φ(x)＝ex－x－1(x≥0)，则φ′(x)＝ex－1≥0，故h′(x)单调递增，h′(x)≥h′(0)＝0，故函数h(x)单调递增，h(x)≥h(0)＝0，由h(x)≥0可得ex－x2－x－1≥0恒成立，故当x∈(0,2)时，g′(x)>0，g(x)单调递增；当x∈(2，＋∞)时，g′(x)<0，g(x)单调递减；10分因此，g(x)max＝g(2)＝，综上可得，实数a的取值范围.12分(1)求出f′(x)即得1分；(2)构造函数g(x)得1分，g′(x)没有分解因式扣1分；(3)讨论时正确写出参数范围即得1分；(4)使用分离参数法酌情给分；(5)计算正确没有最后结论扣1分.