浙教版第一章 解直角三角形综合与测试单元测试课后复习题

这是一份浙教版第一章 解直角三角形综合与测试单元测试课后复习题，共13页。
1．在Rt△ABC中，∠C ＝90°，AC ＝12，BC ＝5，则sinA的值为( D )
A.eq \f(5,12) B.eq \f(12,5)
C.eq \f(12,13) D.eq \f(5,13)
2．[2016·无锡]tan45°的值为( B )
A.eq \f(1,2) B．1 C.eq \f(\r(2),2) D.eq \r(2)
3．[2016·巴中]一个公共房门前的台阶高出地面1.2 m，台阶拆除后，换成供轮椅行走的斜坡，数据如图1所示，则下列关系或说法正确的是( B )
图1
A．斜坡AB的坡比是10°
B．斜坡AB的坡比是tan10°
C．AC＝1.2tan10° m
D．AB＝eq \f(1.2,cs10°) m
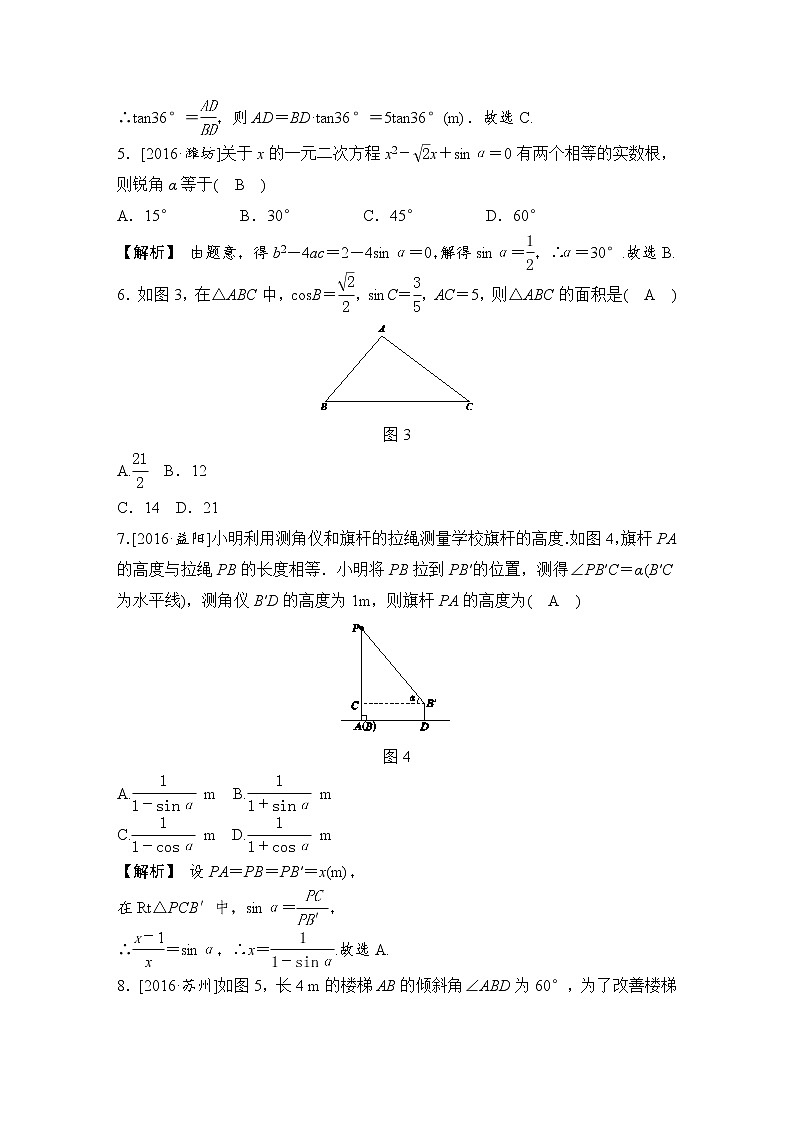
4．[2016·南宁]如图2，厂房屋顶人字形(等腰三角形)钢架的跨度BC＝10 m，∠B＝36°，则中柱AD(D为底边中点)的长是( C )
图2
A．5sin36° m B．5cs36° m
C．5tan36° m D．10tan36° m
【解析】 ∵AB＝AC，AD⊥BC，BC＝10 m，
∴DC＝BD＝5 m，
∵在Rt△ADB中，∠B＝36°，
∴tan36°＝eq \f(AD,BD)，则AD＝BD·tan36°＝5tan36°(m)．故选C.
5．[2016·潍坊]关于x的一元二次方程x2－eq \r(2)x＋sinα＝0有两个相等的实数根，则锐角α等于( B )
A．15° B．30° C．45° D．60°
【解析】 由题意，得b2－4ac＝2－4sinα＝0，解得sinα＝eq \f(1,2)，∴α＝30°.故选B.
6．如图3，在△ABC中，csB＝eq \f(\r(2),2)，sinC＝eq \f(3,5)，AC＝5，则△ABC的面积是( A )
图3
A.eq \f(21,2) B．12
C．14 D．21
7．[2016·益阳]小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图4，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C＝α(B′C为水平线)，测角仪B′D的高度为1m，则旗杆PA的高度为( A )
图4
A.eq \f(1,1－sinα) m B.eq \f(1,1＋sinα) m
C.eq \f(1,1－csα) m D.eq \f(1,1＋csα) m
【解析】 设PA＝PB＝PB′＝x(m)，
在Rt△PCB′中，sinα＝eq \f(PC,PB′)，
∴eq \f(x－1,x)＝sinα，∴x＝eq \f(1,1－sinα).故选A.
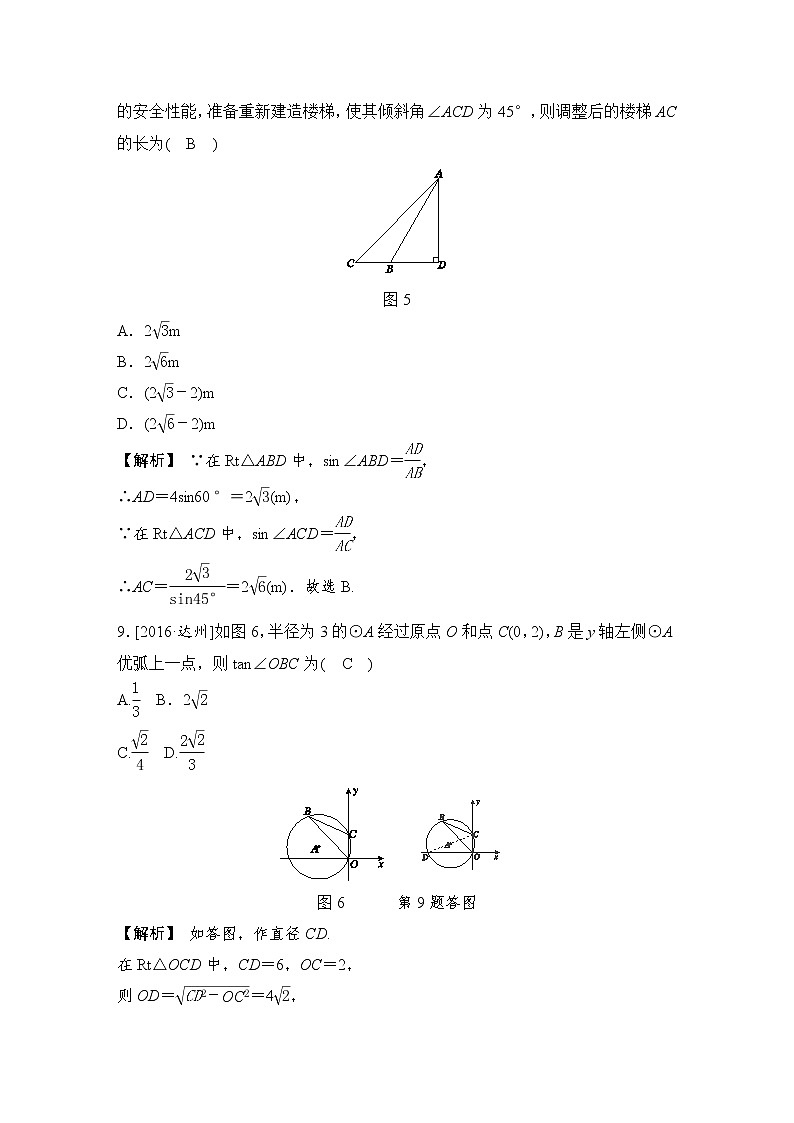
8．[2016·苏州]如图5，长4 m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为( B )
图5
A．2eq \r(3)m
B．2eq \r(6)m
C．(2eq \r(3)－2)m
D．(2eq \r(6)－2)m
【解析】 ∵在Rt△ABD中，sin∠ABD＝eq \f(AD,AB)，
∴AD＝4sin60°＝2eq \r(3)(m)，
∵在Rt△ACD中，sin∠ACD＝eq \f(AD,AC)，
∴AC＝eq \f(2\r(3),sin45°)＝2eq \r(6)(m)．故选B.
9．[2016·达州]如图6，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，则tan∠OBC为( C )
A.eq \f(1,3) B．2eq \r(2)
C.eq \f(\r(2),4) D.eq \f(2\r(2),3)

图6 第9题答图
【解析】 如答图，作直径CD.
在Rt△OCD中，CD＝6，OC＝2，
则OD＝eq \r(CD2－OC2)＝4eq \r(2)，
∴tan∠CDO＝eq \f(OC,OD)＝eq \f(\r(2),4)，
由圆周角定理，得∠OBC＝∠CDO，
则tan∠OBC＝eq \f(\r(2),4).故选C.
10．[2016·重庆B卷]如图7，某办公大楼正前方有一根高度是15 m的旗杆ED，从办公大楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20 m，梯坎坡长是12 m，梯坎坡比i＝1∶eq \r(3)，则大楼AB的高度约为(精确到0.1 m，参考数据：eq \r(2)≈1.41，eq \r(3)≈1.73，eq \r(6)≈2.45.)( D )
A．30.6 m B．32.1 m
C．37.9 m D．39.4 m

图7 第10题答图
【解析】 如答图，AB，DC的延长线交于点G，过点E作EF⊥AB于点F，由图示知AB＝AF＋FB.∵α＝45°，∴∠FAE＝45°，∴AF＝EF.又∵eq \f(BG,GC)＝eq \f(1,\r(3))，BC＝12 m，∴BG2＋(eq \r(3)BG)2＝122，∴BG＝6 m，CG＝6eq \r(3) m．∵FG＝ED＝15 m，DC＝20 m，∴EF＝DG＝(20＋6eq \r(3))m，∴AF＝(20＋6eq \r(3))m，BF＝FG－BG＝DE－BG＝15－6＝9 (m)，∴AB＝20＋6eq \r(3)＋9＝29＋6eq \r(3)≈39.4(m)．故选D.
二、 填空题(每题4分，共24 分)
11．[2015·成都模拟]如图8，在Rt△ABC中，∠C＝90°，AB＝2BC，则sinB的值为 eq \f(\r(3),2) ．
图8
【解析】 ∵AB＝2BC，
∴AC＝eq \r(（2BC）2－BC2)＝eq \r(3)BC，
∴sinB＝eq \f(AC,AB)＝eq \f(\r(3)BC,2BC)＝eq \f(\r(3),2).
12．如图9，小明爬一土坡，他从A处到B处所走的直线距离AB＝4 m，此时，他距离地面高度为h＝2 m，则这个土坡的坡角∠A＝__30°__．
图9
13．在△ABC中，如果∠A，∠B满足|tanA－1|＋eq \b\lc\(\rc\)(\a\vs4\al\c1(csB－\f(1,2)))eq \s\up12(2)＝0，那么∠C＝__75°__．
【解析】 ∵在△ABC中，|tanA－1|＋eq \b\lc\(\rc\)(\a\vs4\al\c1(csB－\f(1,2)))eq \s\up12(2)＝0.
∴tanA＝1，csB＝eq \f(1,2).
∴∠A＝45°，∠B＝60°，
∴∠C＝75°.
14．如图10，△ABC内接于⊙O，AO＝2，BC＝2eq \r(3)，则∠BAC的度数为__60°__．

图10 第14题答图
【解析】 如答图，连结OB，OC，过点O作OD⊥BC于点D.
∵OD⊥BC，
∴BD＝eq \f(1,2)BC＝eq \f(1,2)×2eq \r(3)＝eq \r(3).
在Rt△OBD中，OB＝OA＝2，BD＝eq \r(3)，
∴cs∠OBD＝eq \f(BD,OB)＝eq \f(\r(3),2)，
∴∠OBD＝30°.
又∵OB＝OC，
∴∠OCB＝30°，
∴∠BOC＝120°，
∴∠BAC＝eq \f(1,2)∠BOC＝60°.
15．[2016·福州]如图11，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点．已知菱形的一个角(∠O)为60°，A，B，C都在格点上，则tan∠ABC的值是__eq \f(\r(3),2)__．

图11 第15题答图
【解析】 要求三角函数，必须有直角三角形，构造直角三角形如答图，延长BC到下一格交点处D，连结AD，△BDA即是直角三角形．∵∠O＝60°，小网格是菱形，∴∠ADE＝30°，∠BDE＝60°.∵在Rt△ADC中，eq \f(AD,DC)＝eq \r(3)，
∴tan∠ABC＝eq \f(AD,BD)＝eq \f(AD,2DC)＝eq \f(\r(3),2).
16．[2016·荆州]全球最大的关公塑像矗立在荆州古城东门外．如图12，张三同学在东门城墙上C处测得塑像底部B处的俯角为11°48′，测得塑像顶部A处的仰角为45°，点D在观测点C正下方城墙底的地面上，若CD＝10 m，则此塑像的高AB约为__58__m(参考数据：tan78°12′≈4.8)．

图12 第16题答图
【解析】 如答图，过点C作CE⊥AB于点E，则BE＝DC，
∵∠ECB＝11°48′，
∴∠EBC＝78°12′，
则tan78°12′＝eq \f(EC,BE)＝eq \f(EC,10)≈4.8，
∴EC＝48(m)，
∵∠ACE＝45°，则AE＝EC，BE＝CD＝10 m，
∴AB＝AE＋BE＝58(m)．
∴此塑像的高AB约为58 m.
三、解答题(共66分)
17．(6分)如图13，在坐标平面内有一点P(－2，5)，连结OP.求OP与x轴的负半轴的夹角α的各个三角函数值．
图13
解：∵OP＝eq \r(OA2＋PA2)＝eq \r(22＋52)＝eq \r(4＋25)
＝eq \r(29)，
∴sinα＝eq \f(PA,OP)＝eq \f(5,\r(29))＝eq \f(5,29)eq \r(29)，
csα＝eq \f(OA,OP)＝eq \f(2,\r(29))＝eq \f(2,29)eq \r(29)，
tanα＝eq \f(PA,OA)＝eq \f(5,2).
18．(6分)在△ABC中，∠C＝90°.
(1)若已知a＝3，∠A＝30°，求∠B和b，c；
(2)若已知∠B＝60°，b＝3，求a，c与∠A.
解：(1)∵在△ABC中，∠C＝90°，∠A＝30°，
∴∠B＝60°，sinA＝eq \f(1,2)＝eq \f(a,c)＝eq \f(3,c)，
∴c＝6，
∴b＝eq \r(36－9)＝3eq \r(3)；
(2)∠A＝30°，a＝eq \r(3)，c＝2eq \r(3).
19．(8分)计算：(1)eq \f(cs230°＋cs260°,tan60°·cs30°)＋tan60°；
(2)2cs45°·sin45°－2sin30°·tan45°＋eq \r(6)·tan60°.
解：(1)原式＝eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)))\s\up12(2)＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))\s\up12(2),\r(3)×\f(\r(3),2))＋eq \r(3)＝eq \f(2,3)＋eq \r(3)；
(2)原式＝2×eq \f(\r(2),2)×eq \f(\r(2),2)－2×eq \f(1,2)×1＋eq \r(6)×eq \r(3)＝1－1＋3eq \r(2)＝3eq \r(2).
20．(8分)[2016·梧州]如图14，四边形ABCD是一片水田，某村民小组需计算其面积，测得如下数据：
∠A＝90°，∠ABD＝60°，∠CBD＝54°，AB＝200 m，BC＝300 m.
请你计算出这片水田的面积(参考数据：sin54°≈0.809，cs54°≈0.588，tan54°≈1.376，eq \r(3)≈1.732)．

图14 第20题答图
解：如答图，过点C作CM⊥BD于点M.
∵∠A＝90°，∠ABD＝60°，∴∠ADB＝30°，
∴BD＝2AB＝400 (m)，
∴AD＝eq \r(3)AB＝200eq \r(3)(m)，
∴S△ABD＝eq \f(1,2)×200×200eq \r(3)＝20 000eq \r(3)(m2)，
∵∠CMB＝90°，∠CBD＝54°，
∴CM＝BC·sin54°＝242.7(m)，
∴S△BCD＝eq \f(1,2)×400×242.7＝48 540(m2)，
∴这片水田的面积为20 000eq \r(3)＋48 540＝83 180(m2)．
21．(8分)[2016·黄石]如图15，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB＝800 m，BC＝200m，坡角∠BAF＝30°，∠CBE＝45°.
(1)求AB段山坡的高度EF；
(2)求山峰CF的高度(eq \r(2)≈1.414，CF结果精确到米)．

图15 第21题答图
解：(1)如答图，过点B作BH⊥AF于点H，
∵在Rt△ABH中，sin∠BAH＝eq \f(BH,AB)，
∴BH＝800·sin30°＝400(m)，∴EF＝BH＝400 m；
(2)∵在Rt△CBE中，sin∠CBE＝eq \f(CE,BC)，
∴CE＝200·sin45°＝100eq \r(2)＝141.4(m)，
∴CF＝CE＋EF＝141.4＋400≈541(m)．
答：AB段山坡高度为400 m，山峰CF的高度约为541 m.
22．(10分)[2016·资阳]如图16，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B，C两地相距120海里．
(1)求出此时点A到岛礁C的距离；
(2)若“中国海监50”从A处沿AC方向向岛礁C驶去，当到达点A′时，测得点B在A′的南偏东75°的方向上，求此时“中国海监50”的航行距离(注：结果保留根号)．

图16 第22题答图
解：(1)如答图，延长BA，过点C作CD⊥BA延长线于点D.
由题意，可得∠CBD＝30°，BC＝120海里，
则DC＝60海里，cs30°＝eq \f(DC,AC)＝eq \f(60,AC)＝eq \f(\r(3),2)，
解得AC＝40eq \r(3).
答：点A到岛礁C的距离为40eq \r(3) 海里．
(2)如答图，过点A′作A′N⊥BC于点N，A′E⊥AD于点E.
可得∠1＝30°，∠BA′A＝45°，
则∠2＝15°，即A′B平分∠CBA，∴A′N＝A′E.
设AA′＝x海里，则A′E＝eq \f(\r(3),2)x海里，CA′＝2A′N＝2×eq \f(\r(3),2)x＝eq \r(3)x(海里)，
∴eq \r(3)x＋x＝40eq \r(3)，解得x＝60－20eq \r(3).
答：此时“中国海监50”的航行距离为(60－20eq \r(3))海里．
23．(10分)[2016·苏州]如图17，AB是⊙O的直径，D，E为⊙O上位于AB异侧的两点，连结BD并延长至点C，使得CD＝BD，连结AC交⊙O于点F，连结AE，DE，DF.
(1)证明：∠E＝∠C；
(2)若∠E＝55°，求∠BDF的度数；
(3)设DE交AB于点G，若DF＝4，csB＝eq \f(2,3)，E是eq \(AB,\s\up8(︵))的中点，求EG·ED的值．

图17 第23题答图
解：(1)证明：如答图，连结AD.
∵AB是⊙O的直径，
∴∠ADB＝90°，即AD⊥BC，
∵CD＝BD，∴AD垂直平分BC，
∴AB＝AC，∴∠B＝∠C，
又∵∠B＝∠AED，∴∠AED＝∠C；
(2)∵四边形AEDF是⊙O的内接四边形，
∴∠AFD＝180°－∠AED，
又∵∠CFD＝180°－∠AFD，
∴∠CFD＝∠AED＝55°，
又∵∠AED＝∠C＝55°，∴∠BDF＝∠C＋∠CFD＝110°；
(3)如答图，连结OE.
∵∠CFD＝∠AED＝∠C，∴FD＝CD＝BD＝4，
∵在Rt△ABD中，csB＝eq \f(2,3)，BD＝4，∴AB＝6，
∵E是eq \(AB,\s\up8(︵))的中点，AB是⊙O的直径，∴∠AOE＝90°，
∵AO＝OE＝3，∴AE＝3eq \r(2)，
∵E是eq \(AB,\s\up8(︵))的中点，∴∠ADE＝∠EAB，
∴△AEG∽△DEA，∴eq \f(AE,GE)＝eq \f(DE,AE)，
即EG·ED＝AE2＝18.
24．(10分)[2015·济宁]在一个三角形中，各边和它所对角的正弦的比相等，即eq \f(a,sinA)＝eq \f(b,sinB)＝eq \f(c,sinC)，利用上述结论可以求解如下题目，如：在△ABC中，若∠A＝45°，∠B＝30°，a＝6，求b.
解：在△ABC中，∵eq \f(a,sinA)＝eq \f(b,sinB)，
∴b＝eq \f(asinB,sinA)＝eq \f(6sin30°,sin45°)＝eq \f(6×\f(1,2),\f(\r(2),2))＝3eq \r(2).
理解应用：
如图18，甲船以每小时30eq \r(2) 海里的速度向正北方航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，且乙船从B1处按北偏东15°方向匀速直线航行，当甲船航行20 min后到达A2处时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距10eq \r(2) 海里．
(1)判断△A1A2B2的形状，并给出证明；
(2)乙船每小时航行多少海里？
图18
解：(1)△A1A2B2是等边三角形．
证明：由已知，得A2B2＝10eq \r(2)海里，
A1A2＝30eq \r(2)×eq \f(20,60)＝10eq \r(2)(海里)，∴ A1A2＝A2B2，
又∵∠A1A2B2＝180°－120°＝60°，
∴△A1A2B2是等边三角形；
(2)∵△A1A2B2是等边三角形，
∴A1B2＝A1A2＝10eq \r(2)海里，
∵∠CB1A1＝180°－105°＝75°，
∴∠B2B1A1＝75°－15°＝60°，
又∵∠B1A1B2＝105°－60°＝45°，
∴在△A1B2B1中，eq \f(B1 B2 ,sin45°) ＝ eq \f(A1 B2 ,sin60°)，
B1B2＝eq \f(A1B2,sin60°)·sin45°＝eq \f(10\r(2),\f(\r(3),2))×eq \f(\r(2),2)＝eq \f(20\r(3),3)(海里)，
∴乙船的速度为eq \f(20\r(3),3)÷eq \f(20,60)＝20eq \r(3)(海里/时)．
答：乙船每小时航行20eq \r(3) 海里．