初中第三章 投影与三视图综合与测试单元测试课后复习题

这是一份初中第三章 投影与三视图综合与测试单元测试课后复习题，共10页。
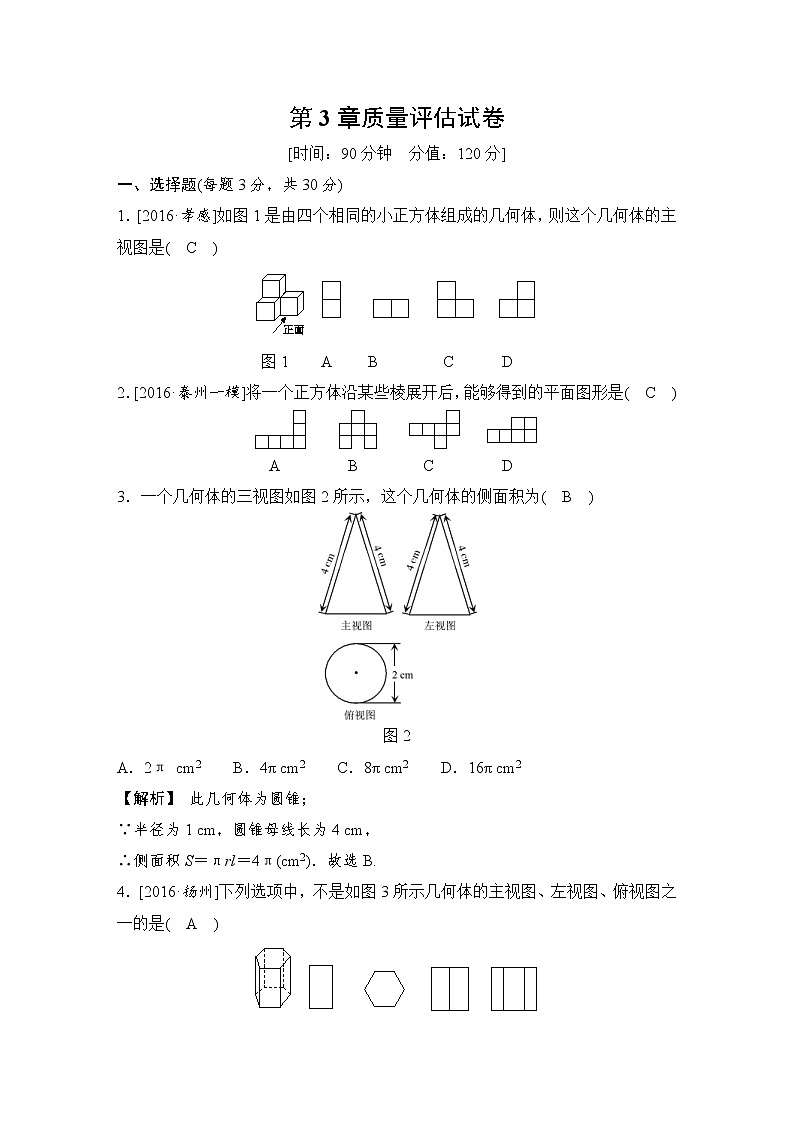
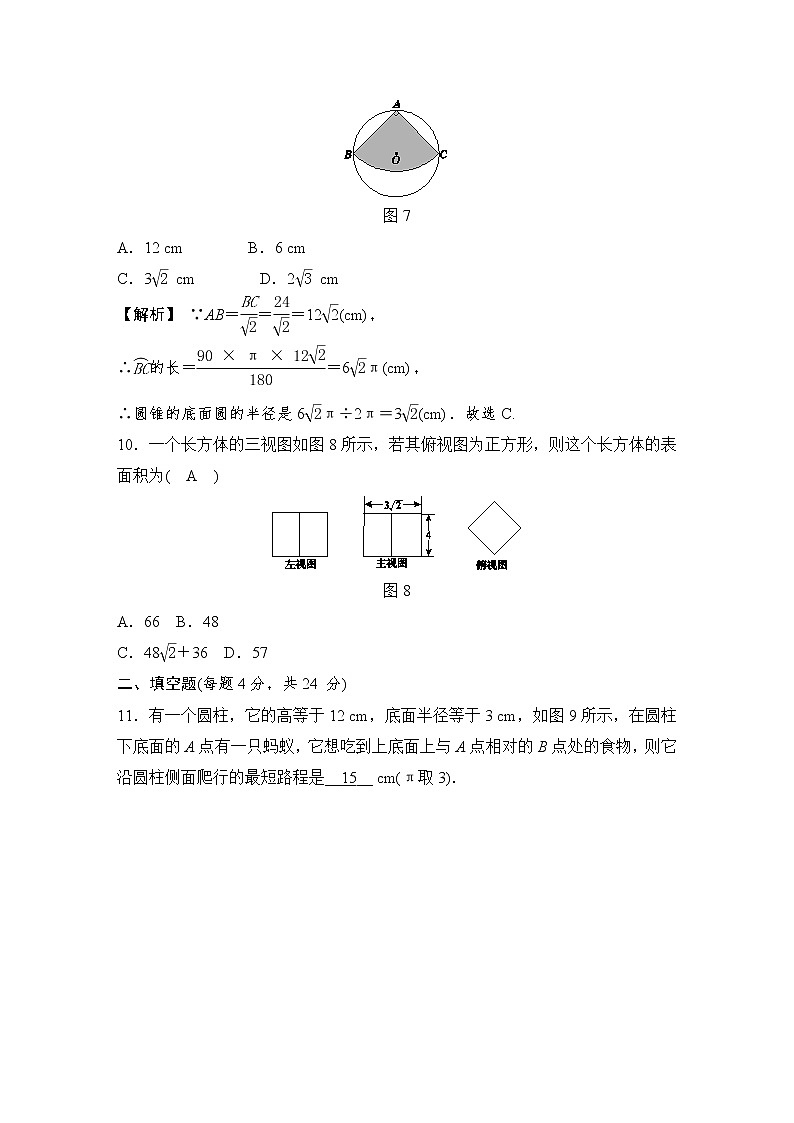
第3章质量评估试卷[时间：90分钟　分值：120分]一、选择题(每题3分，共30分)1．[2016·孝感]如图1是由四个相同的小正方体组成的几何体，则这个几何体的主视图是(　C　)　                图1　　A　　 B　　　　C　　　D2．[2016·泰州一模]将一个正方体沿某些棱展开后，能够得到的平面图形是(　C　)　                 A　　　　 B　　　　C　　　　 D3．一个几何体的三视图如图2所示，这个几何体的侧面积为(　B　)图2A．2π cm2　　B．4π cm2　　C．8π cm2　　D．16π cm2【解析】 此几何体为圆锥；∵半径为1 cm，圆锥母线长为4 cm，∴侧面积S＝πrl＝4π(cm2)．故选B.4．[2016·扬州]下列选项中，不是如图3所示几何体的主视图、左视图、俯视图之一的是(　A　)　               图3　 　A　　　B　　　C　 　　D5．[2016·临沂]如图4，一个空心圆柱体，其主视图正确的是(　B　)　                图4　　　A　　　B　　　C　 　D6．[2016·贺州]已知圆锥的母线长是12，它的侧面展开图的圆心角是120°，则它的底面圆的直径为(　D　)A．2  B．4  C．6  D．87．如图5，某厂生产横截面直径为7 cm的圆柱形罐头，需将“蘑菇罐头”字样贴在罐头侧面．为了获得较佳视觉效果，字样在罐头侧面所形成的弧的度数为90°，则“蘑菇罐头”字样的长度为(　B　)A. cm  B. cmC. cm  D．7π cm图5　　主视图　　　　俯视图图68．如图6是由几个相同的小正方体搭成的几何体的主视图和俯视图，组成这个几何体的小正方体的个数是(　B　)A．5个或6个  B．6个或7个C．7个或8个  D．8个或9个9．[2016·荆门]如图7，从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC，使点A，B，C在圆周上．将剪下的扇形作为一个圆锥的侧面，则这个圆锥的底面圆的半径是(　C　)图7A．12 cm  　　　B．6 cmC．3 cm  　　　D．2 cm【解析】 ∵AB＝＝＝12(cm)，∴的长＝＝6π(cm)，∴圆锥的底面圆的半径是6π÷2π＝3(cm)．故选C.10．一个长方体的三视图如图8所示，若其俯视图为正方形，则这个长方体的表面积为(　A　)图8A．66  B．48C．48＋36  D．57二、填空题(每题4分，共24 分)11．有一个圆柱，它的高等于12 cm，底面半径等于3 cm，如图9所示，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面上与A点相对的B点处的食物，则它沿圆柱侧面爬行的最短路程是__15__ cm(π取3)．
图9【解析】 展开圆柱的半个侧面是矩形，矩形的长是圆柱的底面周长的一半，即3π＝9，矩形的宽是圆柱的高12.根据两点之间线段最短，知最短路程是矩形的对角线的长，即＝15(cm)．12．[2016·聊城]如图10，已知圆锥的高为，高所在直线与母线的夹角为30°，则圆锥的侧面积为__2π__．　图1013．如图11所示是由几个相同的小正方体搭成的几何体的三种视图，则搭成这个几何体的小正方体的个数是__5__．         图11    　　第13题答图【解析】 根据物体的三视图知这个几何体俯视图各位置的小正方体的个数如答图所示，其和为5.14．一个长方体的主视图和左视图如图12所示(单位：cm)，则其俯视图的面积是__6__cm2.【解析】 根据三视图间的关系，由主视图和左视图上的数据可知俯视图的长方形长为3 cm，宽为2 cm，∴俯视图面积是6 cm2.
   图12          　　图1315．如图13是由若干个大小相同的小正方体堆砌而成的几何体，那么其三种视图中面积最小的是__左视图__．16．[2016·抚顺模拟]如图14是一几何体的三视图，则这个几何体的全面积是__33π__．图14【解析】 几何体是圆锥，底面直径是6，则底面周长是6π，母线长是8.则侧面积是×6π×8＝24π，底面面积是9π.则全面积是24π＋9π＝33π.三、解答题(共66分)17．(8分)[2015·崆峒区期末]如图15，已知圆锥底面半径r＝10 cm，母线长为40 cm.(1)求它的侧面展开图的圆心角和面积；(2)若一甲虫从点A出发沿着圆锥侧面绕行到母线SA的中点B，请你动脑筋想一想它所走的最短路线是多少？为什么？　图15　　　　第17题答图解：(1)＝2π×10，解得n＝90.∴圆锥侧面展开图的圆心角为90°，圆锥侧面展开图的面积为π×10×40＝400π(cm2)；(2)如答图，由圆锥的侧面展开图可见，甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长．在Rt△ASB中，SA＝40 cm，SB＝20 cm，∴AB＝20 cm.∴甲虫走的最短路线的长度是20 cm.18．(8分)画出如图16所示物体的三视图．  图16       　    　第18题答图解：如答图所示．19．(10分)[2015·宁德]如图17①是一个蒙古包的照片，这个蒙古包可以近似看成是圆锥和圆柱组成的几何体，如图②所示．(1)请画出这个几何体的俯视图；(2)图③是这个几何体的正面示意图，已知蒙古包的顶部离地面的高度EO1＝6 m，圆柱部分的高OO1＝4 m，底面圆的直径BC＝8 m，求∠EAO的度数(结果精确到0.1°)．①    　　　　　　②　　　　③图17解：(1)俯视图如答图①所示；
        ①    　    　②第19题答图(2)如答图②，连结EO1.∵EO1＝6 m，OO1＝4 m，∴EO＝EO1－OO1＝6－4＝2(m)，∵AD＝BC＝8 m，∴OA＝OD＝4 m，在Rt△AOE中，tan∠EAO＝＝＝，则∠EAO≈26.6°.20．(10分)学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图18，在同一时间，身高为1.6 m的小明(AB)的影子BC长是3 m，而小颖(EH)刚好在路灯灯泡的正下方H点，并测得HB＝6 m.(1)请在图中画出形成影子的光线，并确定路灯灯泡所在的位置G；(2)求路灯灯泡的垂直高度GH.图18解：(1)如答图，CA与HE的延长线相交于点G，即为灯泡所在的位置；第20题答图(2)∵AB∥GH，∴△CBA∽△CHG，∴＝.又∵AB＝1.6 m，BC＝3 m，HB＝6 m，∴＝，∴GH＝4.8，∴路灯灯泡的垂直高度GH为4.8 m.21．(10分)[2016·高阳期末]如图19①所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图②所示，已知展开图中每个正方形的边长为1.(1)求线段A′C′的长度；(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系？并写出过程．①　　　　　　　②　　　图19　第21题答图解：(1)如答图，∵在Rt△A′C′D′中，C′D′＝1，A′D′＝3，由勾股定理，得A′C′＝＝；(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角，∴∠BAC＝45°.如答图，在平面展开图中，连结线段B′C′，由勾股定理，得A′B′＝，B′C′＝.又∵A′B′2＋B′C′2＝A′C′2，∴△A′B′C′为直角三角形．又∵A′B′＝B′C′，∴△A′B′C′为等腰直角三角形．∴∠B′A′C′＝45°.∴∠BAC与∠B′A′C′相等．22．(10分)如图20，有一直径是 m的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形BAC.(1)求AB的长；(2)用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为多少米．　　　图20　　　　　　　第22题答图解：(1)如答图，连结BC.∵∠BAC＝90°，∴BC为⊙O的直径，即BC＝ m，∴AB＝BC＝1(m)；(2)设所得圆锥的底面圆的半径为r(m)，由题意，得2πr＝，解得r＝.答：圆锥的底面圆的半径为 m.23．(10分)[2015·山西]综合与实践：制作无盖盒子．任务一：如图21①，有一块矩形纸板，长是宽的2倍，要将其四个角各减去一个正方形，折成高为4 cm，容积为616 cm3的无盖长方体盒子(纸板厚度忽略不计)．(1)请在图①的矩形纸板中画出示意图，用实线表示剪切线，虚线表示折痕；(2)请求出这块矩形纸板的长和宽．①②　　　　　　　　③　　　　　　　④图21任务二：图②是一个高为4 cm的无盖的五棱柱盒子(直棱柱)，图③是其底面，在五边形ABCDE中，BC＝12 cm，AB＝CD＝6 cm，∠ABC＝∠BCD＝120°，∠EAB＝∠EDC＝90°.(1)试判断图③中AE与DE的数量关系，并加以证明；(2)图②中的五棱柱盒子可按图④所示的示意图，将矩形纸板剪切折合而成，那么这个矩形纸板的长和宽至少为多少厘米？请直接写出结果(图中实线表示剪切线，虚线表示折痕，纸板厚度及剪切接缝处损耗忽略不计)．解：任务一：(1)如答图①所示；　　　　　　           ①　　　　　　　　　 　　②第23题答图(2)设矩形纸板的宽为x (cm)，则长为2x (cm)，由题意，得4(x－2×4)(2x－2×4)＝616，解得x1＝15，x2＝－3(不合题意，舍去)，∴2x＝2×15＝30.答：矩形纸板的长为30 cm，宽为15 cm.任务二：(1)AE＝DE.证明：如答图②，延长EA，ED分别交直线BC于点M，N.∵∠ABC＝∠BCD＝120°，∴∠ABM＝∠DCN＝60°.又∵∠EAB＝∠EDC＝90°，∴∠M＝∠N＝90°－60°＝30°.∴EM＝EN.在△MAB与△NDC中，∴△MAB≌△NDC(AAS)．∴AM＝DN.∴EM－AM＝EN－DN.∴AE＝DE；(2)长至少为(18＋4)cm，宽至少为(4＋8)cm.