中考专题10 几何压轴题2020年中考数学一模分类汇编（山东）（原卷版）

专题10 几何压轴题

一．解答题（共16小题）

1．（2020•市中区一模）在中，，，为中点，点是线段上的一点，点与点、点不重合），连接．将绕点按顺时针方向旋转角，得到△，连接、

（1）如图①，当，在角变化过程中，请证明．

（2）如图②，直线与直线、直线分别交于点，．设，当时，在角变化过程中，是否存在与全等？若存在，求出与之间的数量关系；若不存在，请说明理由；

（3）如图③，当时，点、与点重合．直线与直线相交于点，直线与相交于点．若，设，，求关于的函数关系式．

2．（2020•历下区一模）如图①，在中，，，为边上一点（不与点，重合），将线段绕点逆时针旋转得到，连接，则：

（1）①的度数是　　；

②线段，，之间的数量关系是　　．

（2）如图②，在中，，，为边上一点（不与点，重合），将线段绕点逆时针旋转得到，连接，请判断线段，，之间的数量关系，并说明理由；

（3）如图②，与交于点，在（2）条件下，若，求的最小值．

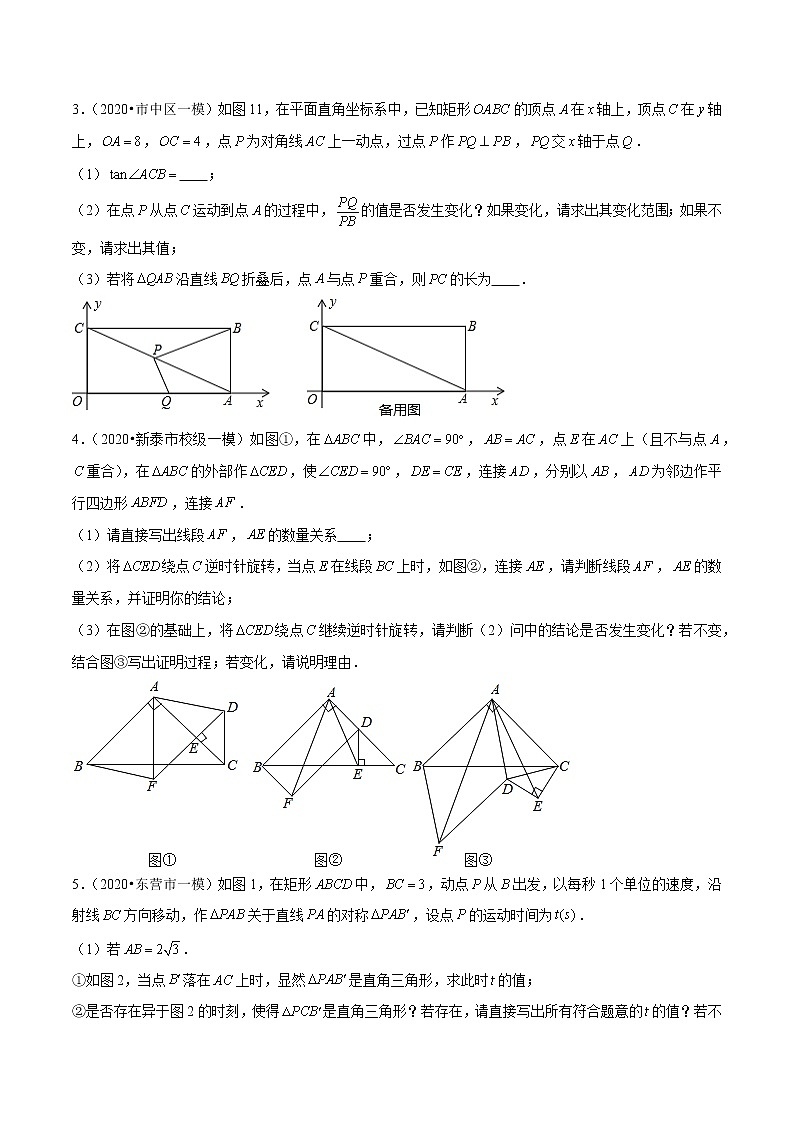
3．（2020•市中区一模）如图11，在平面直角坐标系中，已知矩形的顶点在轴上，顶点在轴上，，，点为对角线上一动点，过点作，交轴于点．

（1）　　；

（2）在点从点运动到点的过程中，的值是否发生变化？如果变化，请求出其变化范围；如果不变，请求出其值；

（3）若将沿直线折叠后，点与点重合，则的长为　　．

4．（2020•新泰市校级一模）如图①，在中，，，点在上（且不与点，重合），在的外部作，使，，连接，分别以，为邻边作平行四边形，连接．

（1）请直接写出线段，的数量关系　　；

（2）将绕点逆时针旋转，当点在线段上时，如图②，连接，请判断线段，的数量关系，并证明你的结论；

（3）在图②的基础上，将绕点继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．

5．（2020•东营市一模）如图1，在矩形中，，动点从出发，以每秒1个单位的速度，沿射线方向移动，作关于直线的对称，设点的运动时间为．

（1）若．

①如图2，当点落在上时，显然是直角三角形，求此时的值；

②是否存在异于图2的时刻，使得是直角三角形？若存在，请直接写出所有符合题意的的值？若不存在，请说明理由．

（2）当点不与点重合时，若直线与直线相交于点，且当时存在某一时刻有结论成立，试探究：对于的任意时刻，结论“”是否总是成立？请说明理由．

6．（2020•历城区一模）如图1．在中，，，点、分别在边、上，．连接，点、、分别为、、的中点．

（1）图1中，线段与的数量关系是　　，位置关系是　　；

（2）把绕点逆时针方向旋转到图2的位置，连接，判断的形状，并说明理由；

（3）把绕点在平面内自由旋转，若，，请直接写出面积的最大值．

7．（2020•新泰市西部一模）已知正方形的对角线，相交于点．

（1）如图1，，分别是，上的点，与的延长线相交于点．若，求证：；

（2）如图2，是上的点，过点作，交线段于点，连结交于点，交于点．若，

①求证：；

②当时，求的长．

8．（2020•青州市一模）如图1，在中，，，点，分别在边，上，，连接，点，，分别为，，的中点．

（1）观察猜想：

        图1中，线段与的数量关系是　 　，位置关系是　 　；

（2）探究证明：

       把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由；

（3）拓展延伸：

       把绕点在平面内自由旋转，若，，请直接写出面积的最大值．

9．（2020•沂源县一模）和是两个全等的等腰直角三角形，，的顶点与的斜边的中点重合，将绕点旋转，旋转过程中，线段与线段相交于点，线段与射线相交于点．

（1）如图①，当点在线段上，且时，求证：；

（2）如图②，当点在线段的延长线上时，求证：；

（3）在（2）的条件下，，，则的长为　　．

10．（2020•岱岳区一模）如图，在四边形中，平分，，是的中点，．

（1）求证：；

（2）过作，并延长至点，使．

①若点是点关于的对称点，点为的中点，求证：；

②若，求证：四边形是菱形．

11．（2020•平邑县一模）将两个全等的和按图①方式摆放，其中，，点落在上，所在直线交所在直线于点．

（1）求证：；

（2）若将图①中的绕点按顺时针方向旋转角，且，其它条件不变，请在图②中画出变换后的图形，并直接写出，，之间的数量关系；

（3）若将图①中的绕点按顺时针方向旋转角，且，其它条件不变，如图③．你认为（2）中猜想的，，的数量关系还成立吗？若成立，写出证明过程；若不成立，请写出，与之间的关系，并说明理由．

12．（2020•郯城县一模）已知是等腰三角形，．

（1）特殊情形：如图1，当时，有　　．（填“”，“ ”或“”

（2）发现探究：若将图1中的绕点顺时针旋转到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．

（3）拓展运用：如图3，是等腰直角三角形内一点，，且，，，求的度数．

13．（2020•金乡县一模）如图，在直角坐标系中，矩形的顶点、分别在轴和轴正半轴上，点的坐标是，点是边上一动点（不与点、点重合），连结、，过点作射线交的延长线于点，交边于点，且，令，．

（1）当为何值时，？

（2）求与的函数关系式，并写出的取值范围；

（3）在点的运动过程中，是否存在，使的面积与的面积之和等于的面积？若存在，请求的值；若不存在，请说明理由．

14．（2020•兖州区一模）综合实践

问题情境

在综合实践课上，老师让同学们以“菱形纸片的剪拼”为主题开展数学活动，如图（1），将一张菱形纸片沿对角线剪开，得到和

操作发现

（1）将图（1）中的以为旋转中心，顺时针方向旋转角得到如图（2）所示，分别延长和交于点，发现．请你证明这个结论．

（2）在问题（1）的基础上，当旋转角等于多少度时，四边形是菱形？请你利用图（3）说明理由．

拓展探究

（3）在满足问题（2）的基础上，过点作，与交于点．试判断、与的数量关系，并说明理由．

15．（2020•嘉祥县一模）如图1，点为射线上一动点且四边形是正方形，请阅读下列内容，并解答下列问题：

（1）如果，．

①当点在线段上时（与点不重合），如图2，线段、之间的位置关系为　 　，数量关系为　 　．

②当点在线段的延长线上时，如图3，①中的结论是否仍然成立，为什么？

（2）如果，，点在在线段上运动，试探究：当满足一个什么条件时，（点、重合除外）？画出相应图形，并说明理由．（画图不写作法）

16．（2020•新泰实验中学一模）如图（1）所示：等边中，线段为其内角角平分线，过点的直线于交的延长线于．

（1）请你探究：，是否都成立？

（2）请你继续探究：若为任意三角形，线段为其内角角平分线，请问一定成立吗？并证明你的判断．

（3）如图（2）所示中，，，，交于点，试求的值．